Задача: в кубе abcd a1b1c1d1 с ребром 2 точки m — середина ребра a1d1. Найти расстояние от точки c до плоскости ab1mГеометрический способ.

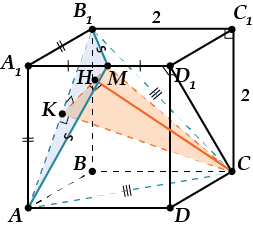1. Куда же опускается перпендикуляр из точки C на плоскость AB1M?

2. Смотрим на ΔAB1M – оказывается, он равнобедренный — B1M=AM!

3. Проведём CA и CB1. Зачем? А они тоже равны CA  и CB1.

4. Отметим k — середину AB1 и проведём MK и CK. Треугольники AB1M и AB1C — равнобедренные, поэтому MK⊥AB1 и CK⊥AB1.

5. И вот теперь! Стереометрическая теорема идёт в ход: признак перпендикулярности прямой и плоскости.

{AB1⊥MKAB1⊥CK⇒AB1⊥CMK.

6.Остался один шаг: проведём CH⊥MK (в плоскости CMK, естественно Угол между плоскостями Взаимное расположение плоскостей

1. 

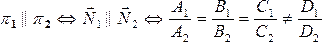
2. 

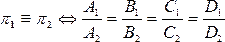
3. 

 

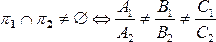
М₀(х₀; у₀; z₀)Îp, p: Ax+By+Cz+D=0

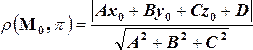 (40)

Если p₁ || p₂, то их общие уравнения имеют вид

p_i: Ах+Ву+Cz+D_i=0, i=1,2 и тогда

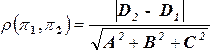(41)

Пусть плоскости p1 и p2 в пдск Оxyz заданы уравнениями:

Углом между двумя плоскостями называют угол j между любыми двумя нормальными векторами плоскостей. Величина угла определяется по формуле: Для нахождения острого угла следует взять модуль правой части.

Условие перпендикулярности двух плоскостей:

 Составить уравнение плоскости a, параллельной плоскости Oxz и проходящей через точку М₀(2;-5; 3).

Решение: По условию задачи a || Oxz Поскольку координаты точки М₀(2;-5;3) удовлетворяют уравнению плоскости Þ или Ответ: .

Условия параллельности и перпендикулярности двух плоскостей

Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости.

Определение 1.Уравнение с тремя переменными Ax + By + Cz + D = 0, где A, B и C не равны 0 одновременно, называется общим уравнением плоскости.

Основные виды уравнений плоскости в трехмерном пространстве:

1) z = 0 - уравнение плоскости Oxy;

2) y = 0 - уравнение плоскости Oxz;

3) x = 0 - уравнение плоскости Oyz;

4) Cz + D = 0 - уравнение плоскости, параллельной плоскости Oxy;

5) By + D = 0 - уравнение плоскости, параллельной плоскости Oxz;

6) Ax + D = 0 - уравнение плоскости, параллельной плоскости Oyz;

7) Ax + By + D = 0 - уравнение плоскости, параллельной оси координат Ox;

8) Ax + Cz + D = 0 - уравнение плоскости, параллельной оси координат Oy;

9) Ax + By + D = 0 - уравнение плоскости, параллельной оси координат Oz;

10) Ax + By + Cz = 0 - уравнение плоскости, проходящей через начало координат.

Теорема 1.Любая плоскость в трехмерном пространстве может быть задана общим уравнением.

Определение 2. Вектор (A, B, C) называется общим нормальным вектором плоскости Ax + By + Cz + D = 0.

Если две плоскости заданы общими уравнениями A₁x + B₁y + C₁z + D₁ = 0и A₂x + B₂y + C₂z + D₂ = 0, то:

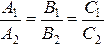- плоскости параллельны тогда и только тогда, когда их нормальные векторы коллинеарны: ;

- плоскости перпендикулярны тогда и только тогда, когда скалярное произведение их нормальных векторов равно нулю: A1A2 + B1B2 + C1C2 = 0.

A(x-x0) + B(y-y0) + C(z-z0) = 0 - уравнение прямой, проходящей через точку (x0, y0, z0), перпендикулярно нормальному вектору.

Различные виды уравнений прямой в пространстве.

1. Параметрические уравнения прямой в пространстве имеют вид

(18.1) ,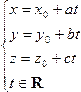

где М₀(х₀,y₀,z₀) – точка, лежащая на прямой, а l(a,b,c) – ее направляющий вектор. Их вывод копирует соответствующие рассуждения из §13. Проведите его сами.

2. Канонические уравнения прямой в пространстве. Вспомним еще раз, что точка М(х,у,z) лежит на прямой l = [М₀(х₀,у₀,z₀), l(a,b,c)] тогда и только тогда, когда M₀M || l, что равносильно пропорциональности координат этих векторов. Если все три координаты вектора l не равны 0, эту пропорциональность можно записать в виде

(18.2) . (18.2).

Это и есть каноническое уравнение прямой в пространстве. Оно аналогично опасной форме (13.5) канонического уравнения прямой на плоскости.

Заметим, что тройное равенство (18.2) есть краткая запись трех попарных равенств: ,и. Поскольку каждое из них является следствием двух других, тройное равенство (18.2) равносильно системе двух обычных, например

(18.3) ,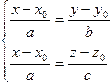

которая называется системой канонических уравнений прямой в пространстве. Приведя первое из них к виду bx – ay + (ay₀ + bx₀) = 0, убедимся, что оно задает плоскость, параллельную Оz. Аналогично, второе уравнение системы (18.2) задает плоскость, параллельную Oy. Таким образом, система канонических уравнений задает прямую, как пересечение двух плоскостей, параллельных двум различным координатным осям.

Система (18.3), как и уравнение (18.2), имеет смысл только при a, b, c ¹ 0. Покажем, как будут выглядеть канонические уравнения прямой, если это условие не выполняется.

Случай 1: a, b ¹ 0, c = 0. В этом случае направляющий вектор l(a,b,0) прямой по признаку (17.8) параллелен плоскости z – z₀ = 0, а сама прямая, имеющая с этой плоскостью общую точку М₀(х₀,y₀,z₀), лежит в ней. Поэтому мы можем, сохранив первое из уравнений (18.3), заменить второе уравнением z – z₀ = 0. Получится система

(18.3') ,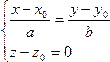

задающая прямую как пересечение плоскостей, параллельных Oz и Оху.

Случай 2: a ¹ 0, b, c = 0. Тут направляющий вектор l(a,0,0) параллелен плоскостям z – z₀ = 0 и у – у₀ = 0, а сама прямая есть их пересечение и задается системой

(18.3'') .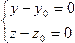

(18.3) Замечание. Форма записи (18.2) канонического уравнения прямой в пространстве весьма коварна. Кроме желания использовать ее, когда какой-то из знаменателей обращается в нуль, она провоцирует еще на одну ошибку: записать условие, что точка (x,y,z) не лежит на прямой, в виде

(18.4) 

Так делать нельзя, ибо отрицание системы (18.3) – а, тем самым, и тройного равенства (18.2) – есть дизъюнкция или, а не конъюнкция (18.4).

3. Уравнения прямой, заданной в пространстве двумя точками, получаются из уравнений (18.1) и (18.2) так же, как в случае прямой на плоскости. Выведите их сами.