
- •1.1.Матрицы и математические действия с ними
- •1.2.Определители и их свойства
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •2.Векторная алгебра
- •3.1.Уравнение линий и поверхностей
- •1. Матрицы, определители и системы линейных уравнений
- •1.1.Матрицы и математические действия с ними
- •1.2.Определители и их свойства
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •2. Векторная алгебра
- •2.2.Скалярное произведение векторов
- •3.1.Уравнения линий и поверхностей

32
→ |
|
|
1 |
|
→ |
→ |
→ |
|
→ |
→ |
|
→ |
|
a |
|
= |
(ax |
i |
+ay j +az |
k |
)= |
i |
Cosα + j Cos β |
+ |
k |
Cos γ . |
|
о |
a2x + a2y + a2z |
||||||||||||
|
|
|
|
|
|
→ →
Угол между векторами Cos ф= a→ b→ .
a b
Проверка параллельности и перпендикулярности векторов. Вычисление площадей многоугольников, разбиением их на
треугольники и используя равенство из геометрической интерпретации
|
|
|
|
|
|
|
|
|
|
|
→ |
→ |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
k |
|
|
векторного произведения. Имеем S =0,5 |
|
ax |
ay |
az |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
bx |
by |
bz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
Расстояние от точки Мо(хо;уо) до прямой с вектором АВ. |
|||||||||||||||
|
|
|
uuuuur uuur |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
AM |
o |
, AB |
|
|
|
|
|
|
|
||||
d= |
|
|
|
|
|
|
|
.Используя рисунок, видно, что числитель – это площадь, |
|||||||
|
|
|
uuur |
|
|
||||||||||
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uur uuuuur а знаменатель – это основание параллелограмма со сторонами ÀÂ и
ÀÌ î .
3.Аналитическая геометрия.
Отличительной особенностью разделов аналитической геометрии является принцип манипулирования с формулами , истолковывая действия как геометрические преобразования некоторых геометрических объектов. Важно усвоить этот принцип и тогда решение задач принимает простой и интересный процесс.
3.1.Уравнения линий и поверхностей
Опред. Множество (совокупность, семейство) точек плоскости с введенной системой декартовых координат, координаты каждой из которых удовлетворяют уравнению F(x,y)=0, называют линия на плоскости, а само уравнение – уравнением этой линии.
Комментарий. Даже в случае отсутствия фактической линии в аналитической геометрии уравнение принято называть уравнением линии. Например, уравнение х2+у2+9=0 только внешне похоже на уравнение

33
окружности, а фактически таковой не представляет. И тогда его называют уравнением мнимой окружности.
Следуя определению, можно рассматривать два типа задач: 1-й тип – дано уравнение и требуется изобразить линию;
2-й тип – дано описание линии и требуется по этому описанию составить(вывести, получить) уравнение линии.
Первый тип частично решен еще в школьном курсе и частично будет решаться в разделах 3 и 4. Второй тип решается всегда по одной и той же схеме:
1-й шаг – берем произвольную точку М(х;у) и предполагаем, что она принадлежит искомой линии; 2-й шаг – математическими средствами связываем координаты точки М и
характеристики линии из ее описания и получаем уравнение линии.
В некоторых случаях вместо указанных двух этапов используют готовые шаблоны уравнений. Делают это если такие шаблоны есть в наличии (см. 6.2,6.4).
Пример 6.1. Составить уравнение линии, каждая точка которой равноудалена от концов отрезка АВ, где А(-1;0), В(3;0).
Решение. Из геометрии известно, что искомая линия – серединный перпендикуляр. Получим его уравнение. Возьмем М(х;у). Пусть М принадлежит искомой линии. Тогда справедливо равенство АМ=ВМ. Фактически мы уже записали уравнение линии. Остается его преобразовать к
виду |
F(x,y)=0. Известно, что |
АМ= ( x + 1) 2 + ( y − 0 ) 2 . Аналогично |
ВМ= |
( x −3)2 + ( y −0)2 . Получаем |
( x +1)2 + ( y −0)2 = ( x −3)2 + ( y −0)2 . |
Полученное гораздо ближе к требуемому. Остаетс преобразовать его и получить окончательно х=1.
Опред. Множество точек пространства с введенной системой координат, координаты каждой из которых удовлетворяют уравнению F(x,y,z)=0 , называют поверхностью. А уравнение – уравнением поверхности в пространстве.
Для этого определения справедливы те же задачи, что и выше как и схема их решений.
F1(x, y, z) = 0,
Опред. Систему принято называть уравнениями линии в
F2 (x, y, z) = 0
пространстве.
Как видим, для линии следует говорить ‘уравнения линии’.
Опред. Алгебраическими линиями(поверхностями) называют линии (в пространстве или на плоскости), уравнения которых представлены полиномами от переменных.
Опред. Порядок линии (поверхности) – это суммарная наивысшая степень переменных в каждом слагаемом полинома.
3.2.Уравнение 1-й степени на плоскости
|
34 |
Пусть в декартовой системе координат на плоскости задано уравнение |
|
Ax+By+C=0. |
(6.1) |
Выясним соответствующий ему геометрический образ. |
|
1. Если A ≠0, B |
≠0, то из (6.1) получаем y=kx+b. Известно, что это |
уравнение прямой с угловым коэффициентом .
2.Если A =0, B ≠0, то из (6.1) получаем х=хо . Это уравнение прямой, перпендикулярной оси Ох.
3.Если A ≠0, B =0, то из (6.1) получаем у= уо . Это уравнение прямой, перпендикулярной оси Оу.
Т.о. уравнение прямой для любых коэффициентов А и В. Само (6.1) называют –
общее уравнение прямой на плоскости.
Для других нужд в аналитической геометрии используют уравнения прямой, записанное в других видах – шаблоны. Каждый из таких шаблонов является решением задачи тип 2 и существенно упрощает решения более крупных задач. Следует иметь представления об этих шаблонах и знать возможные переходы между ними(преобразование одного шаблона в другой).
Уравнение прямой, проходящей через данную точку Мо(хо;уо )
→
перпендикулярно данному вектору N (А;В). Его легко получить решая задачу
типа 2 : вектор Ммо ортогонален вектору N. А потому имеем в координатной форме условие ортогональности А(х-хо)+В(у-уо)=0. Переход от этого уравнения к (6.1) прост – раскрыть скобки и привести подобные. И тгда становится ясно, что числа А и В в (6.1) – координаты нормального вектора к прямой. А сисло С – характеризует точку, через которую проходит прямая.
Уравнение прямой , проходящей через две заданные точки Мо(хо;уо ) и
М1(х1;у1 ). Легко получается при решении задачи тива 2, в которой использовано
условие коллинеарности векторов М Мо и Мо М1 |
. Получаем |
x − xo |
= |
y − yo |
, где |
|
|
||||
uuuuuur |
|
m |
n |
||
m,n – координаты вектора Ì î Ì 1 . |
|
|
|
|
|
Каноническое уравнение прямой r– прямой, которая проходит через данную
точку Мо(хо;уо) параллельно вектору S (m;n).
Нормальное уравнение прямой . xCosα +ySinα -p=0.
Каждый из этих шаблонов используют при решении разных задач. Например, требуется вычислить расстояние от точки Мо(хо;уо ) до прямой Ax+By+C=0. Для
|
|
|
|
|
|
→ |
|
|
|
→ |
||
|
|
|
|
|
|
|
|
|
а no - единичная нормаль к |
|||
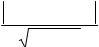
решения используем Рис 6.1. Пусть N - нормаль, |
||||||||||||
прямой Ах+Ву+С=0. Тогда расстояние d от Мо до прямой можно найти так : |
||||||||||||
|
→ |
|
|
|
→ |
→ |
|
|
Axo + Byo +C |
|||
|
|
|
|
|
||||||||
|
|
|
|
|||||||||
Мо М1 =d= |
nd |
= |
пр→ прММо |
= |
nММо |
|
= |
A |
2 |
+ B |
2 |
|
|
|
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|

35
Рис 6.1. К расстоянию от точки до прямой
3.3.Уравнения первой степени в пространстве
Опред. Уравнением второго порядка в пространстве (уравнением поверхности 2-го порядка)
называют уравнение вида
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+a41x+a42y+a43z+ a44=0 |
(6.3) |
Мы познакомимся только с уравнением (6.3), в котором |
отсутствуют |
произведения текущих координат. В этом случае имеется возможность выделить полные квадраты по переменным и получить уравнение поверхности в каноническом виде. Последние и будем изучать более подробно.
Для исследования канонических уравнений поверхностей второго порядка используют метод сечений. В самом простом виде он выглядит так: проводят серии плоскостей, параллельных координатным плоскостям и по результатам (виду сечений) делают вывод о форме поверхности. Эта работа похожа на работу томографа при исследовании внутренних органов человека в медлабораториях или работу топографа при топографической съемке местности.
Реализуем |
метод |
при построении поверхности |
x2 |
+ |
y2 |
+ |
z2 |
=1.Рассечем |
||||
a2 |
b2 |
|
||||||||||
поверхность плоскостями z=h. Тогда в сечении получим |
|
|
c2 |
|||||||||
|
|
|
|
|
|
|||||||
|
x2 |
+ |
y2 |
=1- h2 , |
Из этой системы видно, что h |
не может превышать |
||||||
|
a2 |
|
b2 |
|
c2 |
|
|
|
|
|
|
|
z=h. |
|
|
с. Что означает – поверхность расположена между |
|||||||||
двумя |
|
|
|
|
|
|
|
|
|
|||
плоскостями – выше h=-c и ниже h=c. Более того, в сечениях получаются эллипсы, самый большой из которых расположен в плоскости z=0. Чем дальше от плоскости хОу, тем меньше эллипс. И на высоте с эллипс вырождается в точку.
Если провести аналогичные серии плоскостей . параллельных другим координатным плоскостям, то получим похожие выводы. Следовательно, поверхность образована скольжением эллипсов по эллипса и называется трехосным эллипсоидом.
3.4.Уравнения первой степени в пространстве
Всякую плоскость в пространстве геометрически однозначно задать:
36
→
-точкой Мо(хо;уо ,zо;) на плоскости и вектором N (А;В;С) нормальным к ней; -точкой Мо(хо;уо ,zо;) и расстоянием d от начала координат до плоскости; -тремя точками на плоскости; -двумя точками на плоскости и вектором, параллельным ей и т.д.
Во всех случаях – это задачи 2-го типа и решаются они по одной схеме. Пусть
→
плоскость задана точкой Мо(хо;уо ,zо;) и вектором N (А;В;С) нормальным к ней.
→
Тогда возьмем на плоскости точку М(х;у;z). И тогда векторы М Мо и N будут ортогональны и получим А(х- хо)+В(у- уо)+С(z- zо)=0 – уравнение плоскости,
проходящей через заданную точку перпендикулярно вектору. Если раскрыть скобки и привести подобные, то получим общее уравнение плоскости Ах+Ву+Сz+D=0. Из этого уравнения видно, что всякое уравнение первой степени с тремя переменными – уравнение плоскости в пространстве. Можно рассматривать частные его случаи в зависимости от значений коэффициентов А,В,С,D.
Типовые задачи на плоскость в пространстве.
1.Разные виды уравнений и переходы от одного к другому виду. 2.Расстояние от точки до плоскости.
3.Угол между плоскостями (и взаимное расположение плоскостей). 4.Точка пересечения плоскостей.
5.Пучок плоскостей и др. более сложные задачи.
Комментарий. Следует запомнить жестко наиболее простую для аналитической геометрии ситуацию : для поиска уравнения плоскости следует указать точку, через которую полоскость проходит, и вектор, нормальный плоскости.
Прямую линию в пространстве в аналитической геометрии задают в виде
|
|
|
|
А1 х+ В1 |
у+С1 z + D1 |
|
= 0, |
|||
пересечения двух плоскостей |
F1(x, y, z) = 0, |
или |
|
|
||||||
F (x, y, z) = 0 |
|
А х+ В |
2 |
у+С |
2 |
z + D |
2 |
= 0 . |
||
|
2 |
|
|
2 |
|
|
|
|||
Можно того же результата добиться, задав прямую проходящей через две заданные точки Мо(хо;уо ,zо) и М1(х1;у1;z1). Тогда из условий параллельности(коллинеарности) векторов ММо и МоМ1 получим
|
x − xo |
= |
y − yo |
= |
z − zo |
. Если же обозначить вектор МоМ1= |
||||||||
|
x |
− x |
o |
y |
− y |
o |
z |
1 |
− z |
o |
||||
|
|
|
|
|
||||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|||||
канонические |
уравнения прямой в пространстве |
x − xo |
||||||||||||
m |
||||||||||||||
→ |
|
|
|
|
|
|
S |
(m;n;p), то получим |
|||||
= |
|
y − yo |
= |
z − zo |
. |
В |
|
n |
|
||||
|
|
|
p |
|
||
последних двух способах задания прямой в пространстве “потеряны” уравнения двух плоскостей. Комментарием к этому может служить такое указание – мы имеем равенство трех отношений. Так что , фактически, мы имеет даже три плоскости вместо двух (если сравнивать по два разных отношения, то всегда получится уравнение первого порядка в пространстве – уравнение плоскости). Особенностями этих плоскостей будет следующее – каждая из них является проектирующей данную прямую на некоторую координатную плоскость (в

37
каждом уравнении плоскости только две переменные – значит плоскость перпендикулярна координатной плоскости).
Важно уметь делать переход от одного вида уравнения к другому и понимать смысл этих математических действий в геометрии.
Пример 6.2. Найти, если таковая имеется, точку пересечения трех плоскостей
2х+2у+z=19, |
|
|
|
|
|
|
|
|
|
|
|
|
x+2y+4z=31, |
|
|
|
|
Решение.Сразу видно, что ранг основной и расширен- |
|||||||
4x+6y+9z=-2. |
|
|
|
|
|
|
|
|
ной матриц не болше 3 и не меньше 2. Для |
|||
|
|
|
2 |
1 |
|
0 |
|
0 |
1 |
|
||
|
|
|
2 |
|
|
|
||||||
уточнения вычислим |
1 |
2 |
4 |
= |
−7 |
|
−6 |
4 |
=0. Т.о. rancA=2. Для расширенной |
|||
|
|
|
4 |
6 |
9 |
|
−14 |
|
−12 |
9 |
|
|
|
2 |
|
1 |
|
19 |
2 |
1 |
|
|
|
||
|
19 |
|
|
|
|
|
||||||
матрицы имеем |
31 |
2 |
|
4 |
= |
12 |
0 |
3 |
≠0. Т.е. rancA’=3. Система противоречива – |
|||
|
− 2 |
6 |
|
9 |
|
−59 |
0 |
6 |
|
|
|
|
точки пересечения нет. Геометрически это говорит в данном случае о такой ситуации: параллельных плоскостей нет; следовательно плоскости попарно пересекаются и образуют подобие треугольной призмы.
При взаимном расположении прямой и плоскости следует учитывать, что:
→
полскость характеризуется норамлью N и точкой Мо(хо;уо ,zо) на плоскости, а
прямая – направляющим вектором
→ S
(m;n;p) и точкой М1(х1;у1;z1) на прямой .
|
|
|
|
|
|
|
|
|
→ |
→ |
Так, если плоскость параллельна прямой , то имеем всегда N |
S =0, а если |
|||||||||
|
|
|
|
|
|
|
→ |
→ |
|
|
плоскость перпендикулярна прямой,то всегда N коллинеарен S |
. Если требуется |
|||||||||
найти точку пересечения прямой и плоскости, то систему |
|
|
|
|||||||
|
Ах+Ву+Сz+D=0 |
|
|
|
|
|
||||
|
x − xo |
= |
y − yo |
= |
z − zo |
можно (и даже лучше) |
решать |
так: последнее |
||
|
|
|
|
|||||||
|
m |
n |
p |
|
|
|
|
|||
отношение приравнять параметру t; затем выразить через параметр переменные x,y,z (x=mt+ хо, e=nt+yо, z=pt+zо; затем найденное подставить в уравнение плоскости и найти значение параметра t для точки пересечения; после этого вычислить координаты точки пересечения через значение параметра.
3.5.Уравнения 2-й степени на плоскости
Опред. Уравнение 2-го порядка на плоскости называют уравнение вида
a11x2+2a12xy+a22y2+a13x+a23y+a33=0 (6.2)
Первые три слагаемые образуют квадратичную форму и определяют тип кривой 2-го порядка. Начнем изучение этого уравнения в его каноническом виде.
38
Опред. Множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами, равна постоянной 2а, называют эллисом.
Если расположить указанные точки симметрично началу координат и на оси Ох F1 (0;-с) и F2(0;с), то после решения задачи типа 2 получим каноническое
уравнение эллипса |
x2 |
+ |
y2 |
=1. В этом уравнении параметры эллипса а, в, с |
|
a2 |
b2 |
||||
|
|
|
связаны соотношением а2-b2=c2 . Можно рассмотреть геометрический способ построения эллипса – в лист бумаги вколоть две шпильки, связать свободным кольцом нить, одеть кольцо на шпильки, оттянуть карандашом нить и в таком состоянии двигать крандаш вокруг шпилек – он опишет эллипс.
Точки пересечения эллипса с осями координат называют вершинами эллипса. Расстояния от начала координат до вершин называют полуосями эллипса. Полуость, на которой расположены фокусы – а – называется большой полуосью, b – малой.
Отношение 2c/2a=c/a называют эксцентриситет эллипса. Эксцентриситет (бывший центр) характеризует степень вытянутости эллипса вдоль большой полуоси и может принимать значения от 0 до 1. В первом случае эллипс превращается в окружность (a=b), а во втором – эллипс вырождается в отрезок F1F2. Эллипс – одна из классических кривых 2-го порядка.
Опред. Множество точек плоскости, рсазность расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами, равна постоянной 2а, называют гиперболой.
Если расположить указанные точки симметрично началу координат и на оси Ох F1 (0;-с) и F2(0;с), то после решения задачи типа 2 получим каноническое
|
2 |
|
2 |
|
|
|
y |
|
|
уравнение эллипса |
x |
− |
=1. В этом уравнении параметры гиперболы а, в, с |
|
2 |
2 |
|||
|
a |
|
b |
|
связаны соотношением а2+b2=c2 .
Точки пересечения гиперболы с осями координат называют вершинами гиперболы. Обнаруживается, что гипербола пересекает только ось Ох. Но в аналитической геометрии этот факт истолковывают так : гипербола пересекает ось Ох в действительных вершинах A1(-a;0) и A2(-a;0), а ось Оу в мнимых вершинах В1(0;-b) и B2(0;b). Соответственно, расстояния от начала координат до действительных вершин называют действительными полуосями гиперболы, а расстояния от начала координат до мнимых вершин называют мнимыми полуосями гиперболы. Фокусы расположены на действительной полуоси. Отношение 2c/2a=c/a называют эксцентриситет гиперболы. Эксцентриситет может принимать значения от 1 до бесконечности. Гипербола – одна из классических кривых 2-го порядка.
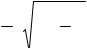
Отметим некоторые особенности построения гиперболы. Из канонического уравнения гиперболы видно, что кривая симметрична относительно обеих координатных осей. Построим ее только в первой четвертию Для этого вычислим
39
ba 2
уиз канонического уравнения y= a x 1− x . Если теперь увеличивать х
неограниченно, то второй сомножитель со временем преврататся в 1 и изменение у будет полностью связано первым множителем. Иначе говоря, с увеличением х гипербола приближается, не пересекая, к прямой у=bx/a. Такую прямую в аналитической геометрии называют асимптотой.
Теперь можно приниматься за построение кривой в таком порядке:
1-й шаг – на плоскости с введенной декартовой системой координат изображаем фокусы и действительные вершины гиперболы (точки пересечения с действительной остью);
2-й шаг – строят “опорный прямоугольник” со сторонами x= ± а , y= ±b ; 3-й шаг – проводят диагонали прямоугольника – асимптоты кривой;
4-й шаг – в первой четверти координатной плоскости , начиная от вершины проводят плавную кривую вне прямоугольника, которая приближается к асимптоте – диагонали и не пересекает ее; 5-й шаг – отражают полученную кривую в координатных осях и получают всю гиперболу.
Опред. Множество точек плоскости, каждая из котрых равноудалена от данной точки F (фокуса) и данной прямой (директрисы), называется параболой.
Если расположить фокус на оси Ох в точке F(p/2;0), а директрису взять в виде х=p/2 и решить задачу типа 2, то получим каноническое уравнение параболы y2=2px.
Отличие такого уравнения параболы от графика квадратного трехчлена чисто символическое – поменялись оси симметрии.
3.6.Уравнения 2-й степени в пространстве
Опред. Уравнением второго порядка в пространстве (уравнением поверхности 2-го порядка)
называют уравнение вида |
|
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+a41x+a42y+a43z+ a44=0 |
(6.3) |
Мы познакомимся только с уравнением (6.3), в котором |
отсутствуют |
произведения текущих координат. В этом случае имеется возможность выделить полные квадраты по переменным и получить уравнение поверхности в каноническом виде. Последние и будем изучать более подробно.
Для исследования канонических уравнений поверхностей второго порядка используют метод сечений. В самом простом виде он выглядит так: проводят серии плоскостей, параллельных координатным плоскостям и по результатам (виду сечений) делают вывод о форме поверхности. Эта работа похожа на работу томографа при исследовании внутренних органов человека в медлабораториях или работу топографа при топографической съемке местности.
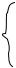
|
|
|
|
|
|
|
|
|
|
40 |
||
Реализуем |
метод |
при построении поверхности |
x2 |
+ |
y2 |
+ |
z2 |
=1.Рассечем |
||||
a2 |
b2 |
|
||||||||||
поверхность плоскостями z=h. Тогда в сечении получим |
|
|
c2 |
|||||||||
|
|
|
|
|
|
|||||||
|
x2 |
+ |
y2 |
=1- h2 , |
Из этой системы видно, что h |
не может превышать |
||||||
|
a2 |
|
b2 |
|
c2 |
|
|
|
|
|
|
|
z=h. |
|
|
с. Что означает – поверхность расположена между |
|||||||||
двумя |
|
|
|
|
|
|
|
|
|
|||
плоскостями – выше h=-c и ниже h=c. Более того, в сечениях получаются эллипсы, самый большой из которых расположен в плоскости z=0. Чем дальше от плоскости хОу, тем меньше эллипс. И на высоте с эллипс вырождается в точку.
Если провести аналогичные серии плоскостей . параллельных другим координатным плоскостям, то получим похожие выводы. Следовательно, поверхность образована скольжением эллипсов по эллипса и называется трехосным эллипсоидом.
3.7.Цилиндры и поверхности вращения
Из поверхностей, отличных от 2-го порядка рассмотрим два частных случая.
Пусть задано уравнение F(x;y)=0 в пространстве. И требуется установить, как выглядит поверхность.
Комментарий. Т.к. сказано, что уравнение задано в пространстве, то отсутствие в уравнении некоторых переменных не противоречит определению поверхности в разделе 6.1.
Рассуждаем так. Добавим к этому уравнению уравнение z=0. Тогда
F (x; y) =0, |
Эта система есть линия на плоскости хОу. На ней можно взять |
|
|
z = 0. |
|
|
|
|
точку М(х;у). Если теперь эту точку перемещать вдоль Oz, не меняя х и у этой
точки, то уравнение поверхности F(x;y)=0 будет тождественно выполняться, т.к.
тождественно выполняется первое уравнение системы. Значит поверхность образована движением прямой, параллельной Oz и пересекающей данную линию
на плоскости. Естественно эту поверхность назвать цилиндрической. У нее две
характеристики, определяющие ее вид : кривая F(x;y)=0 при z=0 – направляющая
цилиндра; и прямая, пересекающая эту кривую, перпендикулярная плоскости расположения кривой и называемая образующей цилиндра.
Вывод : всякое уравнение с двумя переменными в пространстве определяет цилиндрическую поверхность с образующей, параллельной отсутствующей координате и направляющей – кривой в плоскости переменных, записанных в уравнении поверхности.
Пусть дана плоская линия для определенности в плоскости хОу уравнениями
F (x; y) =0, |
На ней можно взять точку М(х;у). Если теперь эту точку |
|
|
z = 0. |
|
вращать около оси Oх, то точка опишет окружность с центром на оси Ох и радиусом, равным у точки М. Уравнение этой окружности Z2+Y2=y2 . В

41
уравнении большими буквами записаны фактически меняющиеся координаты точки на окружности, а малое у – это радиус. Такие же окружности описывают
все точки кривой и образуется поверхность вращения. На каждой окружности этой поверхности х=Х. Если из уравнения окружности выразить у и подставить в
уравнение кривой, то получим F(Х, ± У2 + Z2 )=0. Но последнее уравнение
содержит три переменные и потому является уравнением поверхности вращения взятой в начале линии относительно Ох.
Вывод: если в некотором уравнении квадраты двух переменных имеют одинаковые коэффициенты, то это поверхность вращения. А механизм получения уравнения поверхности , образованной вращением некоторой линии относительно координатной оси, представлен выше.
3.8.Упрощение кривых 2-го порядка
Известно общее уравнение кривой 2-го порядка
a11x2+2a12xy+a22y2+a13x+a23y+a33=0
Известны виды возможных кривых, если кривые заданы каноническими
уравнениями. Рассмотрим более общий случай уравнения
a11x2+2a12xy+a22y2+a13x+a23y+a33=0
Пусть a12=0. Тогда в общем уравнении отсутствует произведение текущих координат. Можно выделить полные квадраты по переменным. Тогда уравнение примет несколько модифицированный вид, но близкий к каноническому.
Построить кривую будет возможно, если использовать известный принцип
сдвига кривой вдоль осей координат.
Если же a12 не равен нулю, тогда механизм упрощения уравнения кривой
несколько усложняется и может быть выполнен в такой последовательности. 1-й шаг – по виду старших слагаемых выписываем матрицу квадратичной формы переменных (см. раздел 1.12); 2-й шаг – составляем и решаем характеристическое уравнение для поиска
собственных значений матрицы квадратичной формы; собственные значения
всегда действительные числа и они укажут нам ти кривой второго порядка (см. раздел 1.11); при этом квадратичная форма принимает канонический вид – в ней не будет произведения текущих координат; следует заметить, что порядок
собственных значений не влияет на тип кривой; 3-й шаг – для известных собственных значаний находим собственные векторы;
нормируем их и получаем новый ортонормированный базис и матрицу поворота
плоскости для перехода к новому базису(см. раздел 1.9); 4-й шаг – строим старый декартов базис и в нем новый декартов базис из
нормированных собственных векторов матрицы квадратичной формы;
5-й шаг – выписываем формулы преобразования координат для перехода к новому базису и преобразуем с их помощью линейные слагаемые в уравнении
кривой; 6-й шаг – теперь в уравнении кривой отсутствует произведение текущих новых
координат и остается выделить полные квадраты по переменным и построить кривую в новой системе координат.
