
- •1.1.Матрицы и математические действия с ними
- •1.2.Определители и их свойства
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •2.Векторная алгебра
- •3.1.Уравнение линий и поверхностей
- •1. Матрицы, определители и системы линейных уравнений
- •1.1.Матрицы и математические действия с ними
- •1.2.Определители и их свойства
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •2. Векторная алгебра
- •2.2.Скалярное произведение векторов
- •3.1.Уравнения линий и поверхностей
4
1.Матрицы, определители и системы линейных уравнений
1.1.Матрицы и математические действия с ними
Определение. Матрицей называют таблицу объектов произвольной структуры, расположенных в виде строк и столбцов.
Обозначают матрицы заглавными латинскими буквами - А, В, ....
Допустимо использование правых нижних и верхних индексов - АТ, А-1 и т.д..
|
a11 |
a12 |
a13 |
. a1,n−1 |
a1n |
|
|
||
|
|
a 21 |
a 22 |
a 23 |
. a 2,n−1 |
|
|
|
|
Фактический вид матрицы |
|
a 2n |
. В этой |
||||||
. |
. |
. |
. . |
. |
. |
|
|||
|
|
|
a m1 |
a m3 |
. a m,n−1 |
|
|
|
|
|
a m1 |
a mn |
|
||||||
матрице m строк и n столбцов. Строго следите за порядком - сначала строка, затем столбец! Говорят: матрица А имеет размерность m на n. Это - первая и простейшая классификация матриц. В частности матрица может быть матрицей-строкой. А также матрицей-столбцом.
Выражения aij - называют элементами матрицы и читают “а-и- жи”. Первый индекс - номер строки, в которой расположен данный элемент; второй индекс - номер столбца, в котором расположен этот элемент. При чтении строго называйте индексы в указанном порядке “ строкастолбец” - этим самым элемент однозначно локализуется в матрице.
По содержанию элементов матрицу тоже классифицируют: если элементы - функции, то матрица функциональная; если элементы - числа, то матрица числовая. Примером матрицы может служить платежная ведомость, понижающий или повышающий трансформатор с двумя обмотками.
Важным частным случаем является единичная матрица, обозначаемая всегда Е , имеющая вид квадратной матрицы нужной в данный
|
1 |
0 |
0 |
. |
0 |
|
|
1 |
0 |
. |
|
|
0 |
0 |
|||
момент размерности |
. . |
. |
. |
. |
|
|
|
|
. |
. |
|
|
. . |
. |
|||
|
|
0 |
0 |
. |
|
|
0 |
1 |
|||
Следующие классы матриц будут введены по необходимости
позднее.
Определение. Две матрицы будем называть равными, если равны их соответствующие элементы.
Это определение указывает, что для сравнения матриц следует: - проверить равенство конфигураций матриц (подразумевается по
умолчанию - “default”);
5
-сопоставить между собой в матрицах все элементы, имеющие
одинаковые индексы.
Все сказанное символически записывают так : А=В aij=bij i,j. Определение. Суммой матриц А и В называют матрицу С, для
которой справедливо соотношение aij+bij =сij i,j.
Это определение указывает, что для суммирования матриц
следует:
-проверить равенство конфигураций;
-суммировать между собой в матрицах все элементы, имеющие одинаковые индексы.
Определение. При умножении матрицы А на величину λ следует на эту величину умножить все элементы матрицы.
Символически λА λaij .
Определение. Матрицы А и В перемножают по правилу
АВ=С сij = ∑a ik bkj .
повcем k
Это определение указывает, что для умножении матриц следует:
-проверить, чтобы число столбцов первой матрицы-сомножителя было равно числу строк второй матрицы-сомножителя;
-выбрать элемент матрицы С, который нужно вычислить - сij;
-поэлементно перемножить строку i матрицы А на столбец j матрицы
Ви результаты просуммировать;
-результат занести в матрицу С на требуемое место.
При практической реализации умножения матрицу С заполняют построчно - так привычней и легче контролировать результат.
Следует отметить, что при умножении матриц не всегда справедлив переместительный закон, т.е. не всегда верно АВ=ВА.
Для дальнейшей работы с матрицами и их применению введем
1.2.Определители и их свойства
Определителем квадратной матрицы А называют число,
символически обозначаемое в компактном виде |
det(A) |
или |
(А). В |
|||
|
a11 |
a12 . |
a1n |
|
|
|
|
|
|
||||
развернутом виде определитель записывают так |
a21 |
a22 . |
a2n |
|
. |
|
|
. |
. . . |
|
|
|
|
|
an1 |
an2 . |
ann |
|
|
|
Число n называют порядком определителя.
Если в определителе вычеркнуть строку i и столбец j, то останется определитель порядка n-1. Этот определитель называют минором элемента aij и обозначают Мij .
Если минор Мij умножить на (1)i+j , то полученный результат называют алгебраическим дополнением элемента aij. и обозначают Аij.

|
|
|
|
|
|
|
|
|
6 |
||
Для |
вычисления |
определителя |
|
используют |
|
формулу |
|||||
|
|
n |
n |
|
|
|
|
|
|
|
|
(рекуррентную) |
|
(А)= ∑a ijA ij = ∑a ijA ij |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
−3 |
|
1 |
2 |
−1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
Пример 1. 1. Вычислить определители |
; |
2 |
4 |
0 |
|
. |
|||||
2 |
7 |
|
|||||||||
|
|
|
|
|
|
|
−1 |
5 |
0 |
|
|
|
|
|
|
|
|
|
|||||
Решение. |
Для |
первого |
определителя |
|
|
имеем |
|||||
1−3 = (−1)1+11 7 + (−1)1+2 (−3) 2 =13 или
27
1 |
−3 |
|
= (−1)2+1 2 (−3) + (−1)2+2 71 =13. |
Заметим, |
что |
мы |
|
||||||
2 |
7 |
|
|
|
|
|
воспользовались двумя различными схемами, так как схема в определении не оговаривается. Результат, естественно, одинаков.
При вычислении определителя во втором случае мы используем обнаруженный факт. И потому увидим , что для вычисления удобно использовать третий столбец элементов. Причина в том. что при этом сумма из определения на первом шаге будет содержать только одно слагаемое. В самом деле
12 −1
24 0 .= −1 5 0
(−1) |
1+3 (−1) |
2 4 |
+ (−1)1+3 0 |
1 2 |
+ (−1)1+3 0 |
1 |
2 |
= − |
2 4 |
= |
|
|
|
−1 5 |
|
−1 5 |
|
|
2 |
4 |
|
−1 5 |
|
|
= −((−1)1+1 2 5 + (−1)2+2 4(−1) =14 . |
Из |
этих |
примеров вытекает |
|||||||
начальный простой алгоритм вычисления определителя:
1-й шаг - просмотри ряды определителя и выбери тот, в котором много нулей;
2-й шаг - используя определение, запиши сумму для вычисления (раскрой определитель по элементам выбранного ряда); получишь n определителей порядка n-1 в каждом слагаемом;
3-й шаг - для каждого из полученных определителей выполни п.п. 1 , 2,
3.
Для дальнейшего упрощения вычислений рассмотрим несколько свойств определителя.
С1. При замене строк определителя соответствующими столбцами (транспонировании) определитель не меняется.
Для доказательства достаточно представить факт транспонирования и затем раскрыть определитель по выбранному ранее ряду.
7
С2. Все свойства определителя, справедливые для строк, справедливы и для столбцов.
С3. При перестановке двух параллельных рядов местами определитель сменит знак.
Для доказательства, не нарушая общности, проделаем указанное с определителем 2-го порядка. Легко видеть это свойство справедливо. Для произвольного определителя достаточно подсчитать количество смен знаков при перестановке соседних рядов.
С4. Определитель с нулевым рядом равен нулю.
Для доказательства достаточно раскрыть определитель по нулевому ряду , используя определение.
С5. Определитель, у которого два параллельных ряда равны, равен нулю.
Для доказательства переставим местами равные ряды. Тогда по С3 определитель сменит знак. Но он при этом не изменится. Такое возможно только если он равен нулю.
С6. В определителе, у которого элементы ряда имеют общий множитель, этот множитель можно вынести за знак определителя.
Если раскрыть определитель по указанному ряду, то этот множитель можно будет вынести за знак суммы. Затем оставшуюся сумму легко развернуть в определитель , в котором общий множитель будет
вынесен за знак определителя. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример 1.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
2 |
−4 |
|
|
|
1 |
1 |
−2 |
|
= 2(−2) |
|
3 |
4 |
|
=-4* 2 |
|
3 |
4 |
|
=-8*11=-88. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
3 |
4 |
0 |
|
=2 |
|
3 |
4 |
0 |
|
|
|
|
|
|||||||
|
|
−1 |
6 |
0 |
|
|
|
−1 |
6 |
0 |
|
|
|
−1 |
6 |
|
|
|
−1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отметим, что после первого знака равенства был вынесен множитель только из 1-й строки. Из второго столбца вынести ничего при этом нельзя, т.к. а12 уже стал равным 1. Далее по определению был раскрыт определитель по 1-й строке. После чего в полученном определителе 2-го порядка можно вынести множитель 2 из 2-го столбца. При этом знак слагаемого установлен устно во всех случаях.
С7. Определитель, у которого элементы двух параллельных рядов соответственно пропорциональны, равен нулю.
Достаточно из одного из пропорциональных рядов вынести общий множитель и в оставшемся определителе окажется два равных ряда. Далее смотри С5.
С8. Если все элементы некоторого ряда представить как сумму двух слагаемых, то определитель будет равен сумме двух определителей, у которых вместо ряда-суммы будут стоять ряды слагаемых из сумм. Остальные ряды будут одинаковы.
Для доказательства достаточно раскрыть определитель по ряду, состоящему из суммы дыух слагаемых. Затем полученную по определению
8
сумму представить как сумму двух слагаемых, каждое из которых есть соответствующий определитель.
С9. Если к некоторому ряду поэлементно прибавить параллельный ряд, умноженный на некоторое число, то определитель не изменится.
Доказательство следует из С8 и С7.
С10. Сумма произведений элементов ряда на алгебраические дополнения параллельного ряда равна нулю.
При составлении алгебраических дополнений элементов параллельного ряда сами элементы в работе не участвуют. Значит вместо них можно взять что угодно, даже и нули(или элементы ряда, по которому производят раскрытие определителя). В любом случае (по С4 или С5) определитель станет равным нулю.
С11. Можно рекомендовать вычислять определитель 2-го порядка по правилу - произведение элементов главной диагонали минус произведение элементов побочной диагонали.
Указанные свойства удобно использовать при вычислении, анализируя состав элементов. Более практичным является прием “изготовления” нулей, используя указанные свойства. В последнем случае придерживаются алгоритма:
-проанализируйте элементы на наличие числа (1 или -1 или другого небольшого числа);
-пусть имеется 1 в строке k и столбце s;
-составляем новый определитель, у которого строка k взята из исходного определителя;
-последовательно умножаем все элементы строки k на некоторые множители и поэлементно складываем с параллельными строками так, чтобы
встолбце s во всех строках (кроме строки k) образовались нули;
-раскрываем определитель по элементам столбца s (т.к. в нем
только один элемент aks отличен от нуля).
Внимание! Строка k в процессе работы не изменяется, как всякий
инструмент, на острие которого расположен рабочий элемент aks. Пример 1.3. Вычислите определитель
|
1 |
x |
x2 |
x3 |
|
1 |
x |
|
= |
1 |
y y2 |
y3 |
= |
0 |
y − x y2 |
||
1 |
z z2 |
z3 |
0 |
z − x z2 |
||||
|
|
|||||||
|
1 |
t |
t2 |
t3 |
|
0 |
t − x t2 |
|
x2 |
|
x3 |
|
|
− x2 |
y3 − x3 |
= |
||
− x2 |
z3 |
− x3 |
||
|
||||
− x2 |
t3 |
− x3 |
|
|
Поясним выполненное. Первая строка умножена на -1 и сложена поэлементно с остальными. Теперь раскрываем определитель по 1-му столбцу. После чего из 2-го строки можно вынести множитель (y-x) , из 3-ей строки (z-x) и из 4-й вынести (t-x). Получаем в результате
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
1 |
y + x y2 |
+ xy + x2 |
|
|
|
|
|
||||
|
|
|
|
|||||||||||
(y-x) |
(z-x)(t-x) |
|
1 |
z + x |
z2 |
+ xz + x2 |
|
. Если |
теперь 2-ю строку |
|||||
|
|
|
1 |
t + x |
t2 |
+ xt + x2 |
|
|
|
|
|
|||
умножить на -1 и сложить поэлементно с остальными то получим |
||||||||||||||
|
|
|
1 |
y + x |
|
y2 + xy + x2 |
|
|
|
|||||
|
|
|
|
|
||||||||||
= |
(y-x)(z-x)(t-x) |
|
0 |
z − y |
z2 |
− y2 |
+ x(z − y) |
|
. |
Если теперь раскрыть |
||||
|
|
|
0 |
t − y |
t2 |
− y2 |
+ x(t − y) |
|
|
|
||||
определитель по 2-му столбцу, а затем вынести из 2-й строки множитель (z- y) и из 3-й строки множитель (t-y) , то получим
(y-x) |
(z-x)(t-x)(z-y)(t-y) |
|
1 |
z + y + x |
|
=(y-x)(z-x)(t-x)(z-y)(t-y)(t-z). |
|
|
|||||
|
1 |
t + y + x |
|
Другими приемами вычисление результата в таком простом виде практически нереализуемо. А применяется этот определитель Ван-дер-Монда очень широко.
Отметим, что для вычисления определителей 3-го порядка исполь-зуют частное правило “треугольников”, неприменимое в общем случае.
Определение. Квадратную матрицу, определитель которой не равен нулю, называют невырожденной.
1- В противном случае матрицу называют вырожденной
1.3.Системы линейных алгебраических уравнений
Определение системой линейных алгебраических уравнений называют
a11x1 |
|
a12 x2 |
|
a13 x3 |
. a1,n−1xn−1 |
|
a1n xn |
|
b1 |
|
|
|
||||||||||||||
|
|
a 21x1 |
|
a 22 x2 |
|
a 23 x3 |
. a 2,n−1xn−1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
. |
|
|
|
a 2n xn |
= |
b2 |
|
или в развернутом |
|||||||||||||||||
|
. |
|
|
|
|
. |
|
|
. |
|
. |
|
|
. |
|
|
|
. |
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
a m1x1 |
|
a m1x2 |
a m3 x3 |
. a m,n−1xn−1 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
a mn xn |
|
bm |
|
|
||||||||||||||||||
|
|
|
|
a11x1 + a12 x2 |
+ a13 x3 +...+a1n xn |
|
= b1 , |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
a 21x1 + a 22 x2 |
+ a 23 x3 +...+a 2n xn |
= b2 , |
|
|
|
|
|
|
||||||||||||||
виде |
|
|
|
|
|
(1) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
.................................................. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
a |
m1 |
x |
1 |
+ a |
m2 |
x |
2 |
+ a |
m3 |
x |
3 |
+...+a |
mn |
x |
n |
= b |
m |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
В дальнейшем |
|
будем использовать более короткий |
термин |
|||||||||||||||||
“линейные системы”. Наиболее компактный вид линейной системы |
АХ=В, |
|||||||||||||||||||||||||
|
|
|
|
|
a11 |
|
a12 |
|
a13 |
|
. a1,n−1 |
|
a1n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a 21 |
|
a 22 |
a 23 |
|
. a 2,n−1 |
|
|
|
|
|
|
|
|
|
||||||
где |
А = |
|
|
|
|
a 2n |
- |
матрица коэффициентов при |
||||||||||||||||||
. |
. |
|
|
. |
|
. . |
. |
|
|
. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
a m1 a m3 |
|
. a m,n−1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a m1 |
|
|
|
a mn |
|
|
|
|
|
|
|||||||||||

10
x1
неизвестных, которые образуют матрицу-столбец Х= x2 =(х1 х2 ... xn)Т,а
.xn
|
b1 |
|
|
|
|
|
|
|
|
|
|
свободные члены образуют матрицу-столбец В= |
b2 |
|
=(b1 b2... bm) |
T |
. |
. |
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
bm |
|
|
|
|
Как видим, число уравнений в системе не обязательно равно числу неизвестных. При m=n известен из школьного курса математики метод исключения или метод алгебраического сложения для поиска решения этой системы - матрицы-столбца Х, подстановка которого в каждое уравнение обращает это уравнение в верное равенство (тождество). Однако при наличии большого числа уравнений эти методы становятся неприемлемыми с точки зрения объема вычислений. При этом всегда остается вопрос о наличии того, что мы ищем (есть ли вообще искомое решение), а также о количестве таких решений.
Сначала решим вопрос о поиске гарантировано существующего
единственного решения.
1.4.Формулы Крамера
Теорема. Если матрица линейной системы невырождена, то система имеет единственное решение, определяемое по формулам x j = j , где j -
определитель, полученный из |
заменой столбца j матрицей-столбцом |
свободных членов; j=1,2,3,...,m. |
|
Доказательство. Пусть матрица в системе (1) квадратная размерности mm. Умножим в системе первое уравнение на А11, 2-е - на А21 и т.д. последнее - на Аm1. Затем суммируем отдельно левые и правые части всех уравнений. Получим после группировки по общим множителям xj слева x1(a11A11+a21A21+...+am1Am1)+x2(a12A11+a22A21+...+am2Am1)+...
+ xь(a1ььA11+a2ьA21+...+amьAm1) , |
а справа b1A11+b2A21+...+bmAm1 . В |
первой скобке записан определитель |
, вычисленный по элементам 1-го |
столбца. Во 2-й скобке записан нуль по С10, т.к. там записана сумма произведений 2-го столбца на алгебраические дополнения 1-го столбца. Аналогично записана для остальных скобок слева. А справа записано выражение для этого же определителя, первый столбец которого заменен столбцом свободных членов системы. Таким образом получаем равенство
x1 = 1. Откуда получаем x1 = 1 . Теперь можно повторить весь процесс

11
для алгебраических дополнений 2-го столбца. И получим требуемое утверждение теоремы.
Частный случай - однородная система линейных уравнений
a11x1 + a12 x |
2 |
+ a |
13 x3 +...+a1n x m = 0, |
||||||||||||
|
|
|
+ a 22 x |
|
+ a |
23 x3 + +a 2n x m = 0, |
|||||||||
a 21x1 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.................................................. |
|||||||||||||||
a |
x |
1 |
+ a |
m2 |
x |
2 |
+ a |
m3 |
x |
3 |
+...+a |
mn |
x |
m |
= 0, |
m1 |
|
|
|
|
|
|
|
|
|||||||
всегда имеет решение Х=(0 0...0)Т, которое называют тривиальным. Перейдем к другим возможным ситуациям.
1.5.Общий алгоритм решения системы линейных уравнений
Определение. Наибольший из порядков не равных нулю миноров матрицы А называют рангом матрицы и обозначают rankA.
Для поиска ранга используют разные методы. Мы используем метод окаймляющих миноров. Выполним реализацию этого метода на примере.
|
1 |
3 |
−1 |
2 |
|
2 |
−1 |
3 |
|
Пример 1.4. Определить ранг матрицы А= |
5 . |
|||
|
|
10 |
6 |
|
1 |
1 |
|||
Решение. Т.к. в матрице есть элементы (“определители” 1-го порядка), не равные нулю, то делаем вывод: rankA ≥1. рассмотрим элемент а11=1 ≠ 0 и записанный в левом верхнем углу матрицы. Если бы там был записан нуль, то всегда можно переставить местами параллельные ряды матрицы так, чтобы на этом месте был записан ненулевой элемент.
Теперь выпишем возможные окаймляющие миноры для элемента |
|||||||||||||||||||||||||||||||||||||
а11=1 ≠ 0 .Это будут миноры |
|
|
1 3 |
|
, |
|
1 1 |
|
|
|
1 |
2 |
|
, |
|
1 3 |
|
|
, |
|
1 −1 |
|
|
|
1 |
2 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 |
−1 |
|
|
2 |
|
3 |
|
|
, |
|
2 |
5 |
|
|
1 10 |
|
|
|
1 |
6 |
|
|
, |
|
1 |
1 |
|
||||||||
Фактически - эти миноры |
поставляют |
|
|
“забор”, который оградил данный |
|||||||||||||||||||||||||||||||||
элемент “пролетами” из частей рядов |
матрицы. Легко |
видеть, |
что |
уже |
|||||||||||||||||||||||||||||||||
первый из них не равен нулю. Т.е. |
|
|
rankA ≥ 2 . Значит |
|
предстоит |
его |
|||||||||||||||||||||||||||||||
окаймлять, тем более, что |
|
|
он |
записан |
|
|
в |
левом верхнем |
углу. |
Получаем |
|||||||||||||||||||||||||||
окаймляющие миноры для минора М2= |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
1 |
3 |
−1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
. Это будут |
|
|
|
2 |
−1 |
3 |
|
|
и |
|||||||||||||||||||||||||||
|
2 |
−1 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
10 |
6 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
3 |
2 |
|
2 |
−1 |
5 |
. Легко подсчитать. что оба они равны нулю. Т.к. других миноров |
1 |
10 |
1 |
|
3-го порядка, окаймляющих минор М2, нет, то делаем вывод: rankA = 2 . При этом М2 назовем базисным минором матрицы А.
12
Определение. Матрицу А системы (1) называют основной матрицей системы.
Определение. Если к столбцам основной матрицы приписать справа матрицу-столбец свободных членов, то получится матрица, которую называют расширенная матрица системы.
|
|
|
|
a11 |
a12 |
|
|
|
|
a 21 |
a 22 |
|
|
|
|
||
|
Так А = . |
. |
. |
||
|
|
|
|
a m1 |
a m1 |
|
|
|
|
||
|
|
a11 |
a12 |
a13 . |
|
|
|
a 21 |
a 22 |
a 23 . |
|
|
|
||||
А1 = |
. . |
. |
. |
. |
|
|
|
a m1 |
a m1 |
a m3 . |
|
|
|
||||
a13 |
. a1,n−1 |
|
a1n |
|
|
|
a 23 |
. a 2,n−1 |
|
|
|
|
|
|
a 2n |
основная , а |
||||
. |
. |
. |
|
. |
|
|
a m3 |
. a m,n−1 |
|
|
|
|
|
|
a mn |
|
||||
a1,n−1 |
a1n |
b1 |
|
|
|
|
a 2,n−1 |
|
|
|
|
|
|
a 2n b2 |
- расширенная матрицы для |
|||||
. |
. . |
|
||||
a m,n−1 |
|
|
|
|
|
|
a mn b m |
|
|
|
|||
системы (1).
Теорема Кронекера-Капелли. Для того, чтобы система (1) имела решение (была совместима), необходимо и достаточно, чтобы ранги основной и расширенной матриц были равны. (Без доказательства).
На базе этой теоремы построен алгоритм решения системы линейных уравнений (1) :
1-й шаг - выписываем основную А и расширенную А1 матрицы системы;
2-й шаг - определяем(находим) ранги rankA и rankA1 ;
3-й шаг - если rankA = rankA1 , то переходим к шагу 4, иначе делаем
вывод, что система не имеет решения (несовместна); 4-й шаг - выписываем базисный минор;
5-й шаг - отбрасываем уравнения, коэффициенты при неизвестных в которых не вошли в базисный минор;
6-й шаг - неизвестные, чьи коэффициенты не вошли в базисный минор, объявляем свободными (считаем известными величинами) и переносим в столбец свободных членов;
7-й шаг - решаем оставшуюся систему, в которой число уравнений равно числу неизвестных и определителем которой является базисный минор, не равный нулю; Метод решения выбираем по необходимости, т.к. система имеет единственное решение;
8-й шаг - записываем решение исходной системы (1).
Пример 1.5. Решите систему, расширенная матрица которой
|
1 |
3 |
−1 |
|
рассмотрена в примере 4, а основная имеет вид А= |
2 |
−1 |
3 |
. |
|
|
10 |
6 |
|
1 |
|
|||
Решение. В данном случае пропущены шаги 1,2,3, т.к установлены ранги основной и расширенной матриц. И эти ранги равны.
|
|
|
|
|
13 |
Поэтому на шаге 4 выписываем готовый базисный минор М2= |
|
1 |
3 |
|
. Теперь |
|
|
||||
|
2 |
−1 |
|
записываем систему, отбросив третье уравнение и положив свободное
переменное х3=С: x1 + 3x2 |
= 2 + C, |
. Получаем решение этой системы |
||||
|
|
2x1 − x2 |
= 5 − 3C |
|
||
17 − 8C −1 + 5c T |
|
|||||
Х= |
|
|
|
. Его принято называть общим, т.к., полагая |
||
7 |
7 |
|||||
|
|
|
||||
разные значения С, получим разные решения системы. Теперь запишем решение исходной системы с расширенной матрицей А1 из примера 4:
17 − 8C −1 + 5C |
T |
||||
Х= |
|
|
C |
. Ответ: система имеет бесчисленное |
|
7 |
7 |
||||
|
|
|
|||
количество решений, определяемых по формуле для Х.
1.6.Матричный метод решения линейной системы.
Определение. Матрицу А-1 называют обратной для матрицы А, если А- 1 А=А А-1 =Е.
Из определения следует, что матрицы А и А-1 квадратные и для
них
справедлив переместительный закон.
Теорема. Если А невырождена, то обратная матрица существует. Доказательство. Ограничимся квадратной матрицей 2-го порядка.
Пусть имеется некоторая матрица |
А= a11 |
a12 |
. Пусть detA ≠0. Пусть |
||
|
|
a 21 |
a 22 |
|
|
имеется некоторая матрица В= b11 |
b12 |
- неизвестная нам. И пусть АВ=Е , |
|||
|
b21 |
b22 |
|
|
|
где Е= 1 |
0 . Тогда после умножения слева по равенству матриц получаем |
||||
0 |
1 |
|
|
|
|
систему 4-х уравнений с четырьмя неизвестными элементами матрицы В
|
a11b11 |
+ a12 b21 |
=1, |
|
: |
a11b12 |
+ a12 b22 |
= 0, |
, которая фактически распадается на две автономные |
a 21b11 |
+ a 22 b21 |
= 0, |
||
|
a 21b12 |
+ a 22 b22 |
=1, |
|
системы, каждая из которых имеет один и тот же определитель, равный
= |
a11 |
a12 |
≠ 0определителю матрицы А и только по две переменные.: |
|||||||
a 21 |
a 22 |
|||||||||
|
|
|
|
|
|
|
|
|||
a11b11 |
+ a12 b21 |
=1. |
и |
a11b12 |
+ a12 b22 |
= 0, |
Каждую из этих систем можно |
|||
|
|
+ a12 b21 = 0 |
|
+ a12 b22 |
=1. |
|||||
a 21b11 |
|
a 21b12 |
|
|||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
решить, |
например, по |
формулам |
Крамера |
и получить |
ответ в |
виде: |
|||||||
b11 = |
a 22 |
, b21 = |
−a 21 |
, b12 |
= |
−a12 |
,b22 |
= |
a12 |
, в |
числителях |
каждой |
дроби |
|
|
|
|
||||||||||
записано алгебраическое дополнение соответствующих элементов транспонированной матрицы АТ. Доказательство закончено. И из него вытекает алгоритм поиска А-1 :
1-й шаг - вычисли detA;
2-й шаг - если detA не равен нулю, перейдите к пункту 3, иначе обратной матрицы не существует;
3-й шаг - транспонируйте матрицу А; 4-й шаг - для всех элементов транспонированной матрицы выпишите
алгебраические дополнения;
5-й шаг составьте обратную матрицу из отношений detA ijA .
Используя обратную матрицу легко решить линейную систему, если она имеет единственное решение. В самом деле, пусть дана система АХ=В с невырожденной матрицей А (т.е. detA ≠0). Сформируем матрицу А-1 по вышеприведенному алгоритму. Теперь умножим слева обе части уравнение АХ=В на матрицу А-1. Получим А-1АХ= А-1 В. Но А-1 А=Е, а ЕХ=Х и потому получаем Х= А-1В.
Пример 1.6. Решите систему
x1 + 3x2 − x3 = 2, |
|
2x1 − x2 |
+ 3x3 = 5, Ранг основной и расширенной матрицы |
x1 +10x2 |
+ 6x3 =1. |
этой системы равен 2 и потому система имеет решение. Базисный минор системы равен М2 и приведен в примере 5. Фактически нам предстоит
решить систему x1 + 3x2 |
= 2 + C, |
.На этот раз мы решим ее, используя |
2x1 − x2 |
= 5 − 3C |
|
обратную матрицу для последней системы. Так как матрица последней системы невырождена (detA= М2), легко найти ее обратную матрицу А-1
= − |
1 |
−1 |
−3 |
, а потому решение принимает вид Х= − |
1 |
−1 |
−3 |
2 |
+ C |
|||||
|
|
|
|
|
|
|
|
|
||||||
7 |
7 |
|
||||||||||||
|
|
−2 1 |
|
|
|
−2 1 |
5 |
− 3C |
||||||
17 − 8C −1 + 5C T |
17 − 8C −1 + 5C |
|
T |
|||||||||||
= |
|
|
|
|
|
. А для исходной системы Х= |
|
|
|
|
|
|
|
C . |
|
|
7 |
|
|
|
|
|
7 |
|
|
||||
|
|
|
7 |
7 |
|
|
|
|
|
|||||
Ответ: система имеет бесчисленное количество решений, определяемых по формуле для Х.
1.7.Понятие о приближенных методах решения линейных систем
Рассмотренные примеры решения линейных систем являются чисто учебными. На практике (при решении прикладных профессиональных или
15
научных задач) приходится решать чистемы с сотнями , тысячами и даже сотнями тысяч уравнений. Естественно, что выполнить это можно только специальными численными методами. Понятие о некоторых из них и рассматривается в этом разделе. Сразу следует отметить, что эти методы обеспечивают поиск только единственно существующего решения системы. Вопросы обеспечения наличия или отсутствия решения решает тот, кто собирается решать такую систему.
Для линейных систем с несколькими сотнями уравнений используют метод Гаусса (метод последовательного исключения неизвестных в разных вариациях). Для систем с несколькими тысячами уравнений, матрицы которых имеют специальный вид, используют итерационные методы решения(о которых будет сказано ниже). Для большего числа уравнений используют вероятностные методы МонтеКарло).
Пусть систему АХ+В удалось преобразовать к виду Х= А1Х+В1. Если матрица А1 такова, что:
-сумма модулей коэффициентов строки (для всех строк) не превосходит 1;
-сумма модулей коэффициентов столбца (для всех столбцов) не превосходит 1,
тогда можно организовать вычислительный процесс по схеме Х(k+1)= А1Х(k) +В1, где k - номер предыдущего приближения к решению
системы. Этот процесс называют итерационным (повторяющимся) и
продолжают до тех пор, пока |
|
X(k+1) − X(k ) |
|
≤ ε, где ε - требуемая |
|
|
погрешность решения задачи. В качестве приближенного решения системы берут матрицу-столбец Х(k+1) .
Пример 1.7. Методом итераций решить систему
x1 +10x2 − x3 = 2,5x1 − x2 + 3x3 = 5,
x1 +10x2 + 20x3 =1.
Решение. переставим в системе первое и второе уравнение. Затем из первого уравнения найдем х1; из второго - х2 и из третьего х3. В результате
|
|
x1 = |
|
0,2x2 − 0,6x3 +1, |
||||
|
|
|
= −0,1x1 |
+ 0,1x3 + 0,2, |
||||
получим систему вида x2 |
||||||||
|
|
|
= −0,05x1 − 0,5x2 + 0,05. |
|||||
|
|
x3 |
||||||
Теперь организуем итерационный процесс по схеме |
||||||||
x1 |
(k+1) |
= |
0,2x2 |
(k ) − 0,6x3 |
( k ) +1, |
|||
|
(k+1) |
|
( k ) |
|
|
|
( k ) |
+ 0,2, |
= −0,1x1 |
|
+ 0,1x3 |
|
|||||
x2 |
|
|
|
|||||
|
(k+1) |
|
( k ) |
|
|
( k ) |
+ 0,05. |
|
= −0,05x1 |
− 0,5x2 |
|
||||||
x3 |
|
|||||||
|
|
|
|
|
|
|
|
|
16
Проверяем выполнение условий сходимости процесса к точному решению системы. Видим ,что сумма модулей коэффициентов при неизвестных в 1-й строке равна 0,8 , что меньше 1. То же самое верно для
2-й и 3-й строк. Т.о. система обеспечивает сходимость приближений к точному решению.
В эту итерационную схему в качестве нулевого (k=0) приближения в правую часть подставим столбец свободных членов (так чаще всего и делают, хотя можно было брать любой набор для неизвестных)
Х(о) = (1 0,2 0,05) Т .Тогда после вычислений справа получим слева первое (k=1) приближение Х(1) = (1,01 0,105 -0,1) Т. Повторим вычисления и получим последовательно Х(2) = (1,081 0,089 -0,053) Т ;
Х(3) = (1,050 0,087 -0,048) Т ; Х(4) = (1,046 0,090 -0,046) Т; Х(5) = (1,046 0,090 -0,047) Т; Х(6) = (1,046 0,090 -0,048) Т. Мы видим,
Что между 6-м и 5-м приближениями расхождение не превосходит 0,001. Поэтому в качестве решения системы может быть принято шестое приближение Х= Х(6) = (1,046 0,090 -0,048) Т .Это значит : х1=1,046; х2=0,090; х3=-0,046.
1.8.Линейное, евклидово и нормированное пространства.
Определение. Множество М элементов x,y,z…любой природы называют линейным (аффинным, векторным) пространством, если выполнены требования:
1-е. Имеется правило, по которому любым двум элементам х и у из М
ставится в соответствие третий элемент z |
из М, называемый суммой и |
||||
обозначаемый x+y=z. |
|
|
|
|
|
2-е. Имеется правило по которому любому элементу х |
из М |
и |
|||
действительному числу к |
ставится в соответствие |
элемент у |
из |
М, |
|
называемый произведением числа на элемент и обозначаемый кx=y. |
|
|
|||
3-е. Указанные правила подчиняются законам (аксиомам): |
|
|
|||
1* - x+y=y+x: 2* - |
(x+y)+z=x+(y+z); |
3* - |
существует элемент, |
||
называемый нуль элементом и обозначаемый 0, такой, что x+0=x; |
4* - для |
||||
каждого х существует элемент , называемый противоположный и
обозначаемый -х, |
такой что х+(-х)=0; |
5* |
1х=х; |
6* - с(кх)=(ск)х – |
|
сочетательный закон для умножения; |
7* - |
(к+с)х=кх+сх – |
|||
распределительный |
закон умножения |
относительно |
сложения; |
8* - |
|
к(х+у)=кх+ку - распределительный закон сложения относительно умножения.
Если же природа элементов указана так же как и конкретный вид операций, то множество называют конкретным линейным пространством.
Примеры. Множество всех векторов на прямой (на плоскости, в пространстве) , если сложение определено по правилу треугольника (параллелограмма), а умножение на число как деформация, будет линейным векторным пространством с обозначением V1(V2, V3).
17
Множество полиномов степени не выше 2 , если правила суммирования и умножения на число определены как обычно, линейное векторное пространство.
Множество функций, непрерывных на отрезке, множество решений однородной системы и т.д.
Вто же время полиномов степени 2 , если правила суммирования
иумножения на число определены как обычно, не будет линейным векторным пространством, т.к. возможно потеря старшей степени при суммировании таких полиномов (после приведения подобных).
Элементы линейных пространств принято называть векторами. А т.к. умножение производят на действительное число, то еще и действительными.
n
Опред. Выражение ∑ai xi принято называть линейной
i=1
комбинацией элементов (векторов) ЛП.
Опред. Элементы (векторы) {xi} называют линейно
n
независимыми , если их ∑ai xi обращается в нуль тогда и только тогда,
i=1
когда все ai =0.
Опред. Множество {xi} ненулевых линейно независимых векторов (элементов) называют базисом ЛП, если для любого х не из этого множества существуют такие { ai } не все равные нулю, что будет
n
справедливо равенство х= ∑ai xi . Последнее равенство называют
i=1
разложением элемента х в базисе(по базису).
Опред. ЛП называют n-мерным, если в нем существуют n линейно независимых вектора, а n+1 вектор уже будут линейно зависимыми. N называют размерность ЛП и записывают это так dimM=n.
Т.к. иных операций в ЛП не введено, то Опред. Два ЛП называют изоморфными, если между их
элементами установлено взаимно-однозначное соответствие ткк, что, если х и у принадлежат ЛП M и им соответствуют x’ , y’ из ЛП M’, то х+у соответствует x’+y’, а кх соответствует кx’ из М’.
Из последнего следует, что единственной характеристикой ЛП является его размерность. Пишут так Mn.
Опред. Подмножество L из ЛП М, в котором справедливы указанные в определении ЛП операции называют линейным подпространством из Mn.
Определение. Действительное ЛП называют евклидовым, если выполнены требования :
2- имеется правило, по которому любым х и у из ЛП ставится в соответствие действительное число, называемое скалярным произведением и обозначаемое (х,у);

|
|
|
|
|
|
|
|
18 |
3- указанное правило |
подчиняется аксиомам |
: а |
- |
(х,у)=(у,х); |
б – |
|||
(х1+х2)у=х1у+х2у ; с – (кх,у)=к(х,у) для любого к ; |
d – (х,х)>0 , если х не |
|||||||
нулевой и (х,х)=0, если х - нулевой. |
|
|
|
|
|
|||
Примерами евклидова пространства будут уже упоминаемые ранее V1,V2, |
||||||||
V3. |
Примером ЕП будет множество упорядоченных совокупностей Аn, |
|||||||
|
||||||||
если |
операцию |
скалярное произведение |
определить |
по формуле |
(х,у)= |
|||
n |
|
|
|
|
|
|
|
|
∑уi |
xi . |
|
|
|
|
|
|
|
i=1 |
Свойства. Для любых х и у из ЕП справедливо равенство (Коши- |
|||||||
|
||||||||
Буняковсого) |
(х,у)2 ≤(х,х)(у,у). |
|
|
|
(кх-у,кх-у)=к2(х,х)- |
|||
|
Доказательство. |
Согласно аксиомы |
d |
имеем |
||||
2к(х,у)+(у,у) ≥0. Для того , чтобы квадратный трехчлен был неотрицателен при любых значениях переменной к требуется , чтобы дискриминант был неположителен . Получаем (х,у)2-(х,х)(у,у) ≤0. Откуда и следует требуемое.
Опред. ЛП называют нормированным, если выполнены требования :
1- имеется правило, по которому любому х из ЛП ставится в соответствие
действительное число, называемое нормой элемента и обозначаемое |
|
х |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(длиной); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2- это правило подчиняется аксиомам : а - |
|
х |
|
|
|
>0 , если х не нуль и |
|
|
|
х |
|
|
|
=0, если |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
х – нуль-элемент; б - |
|
|
кх |
|
= |
|
к |
|
|
|
|
|
х |
|
|
|
|
|
|
|
для любого действительного к; с – для |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
любых х и у верно |
|
х+ у |
|
≤ |
|
х |
|
|
+ |
|
|
|
у |
|
|
|
- неравенство треугольника. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ЕП |
будет |
|
нормированным, |
если норму определить |
так |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
х |
|
|
|
= (х, х) (корень квадратный из скалярного квадрата). |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Опред. n – элементов ei ≠0 образуют ортонормированный базис в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ЛП, если: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 при i ≠ j, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
а – (ei |
, ei)= 0 при i = j . Получение |
|
|
|
|
|
=1 называют нормированием. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Свойство. Если ЛП ортонормированно с базисом { ei }, то (х,у)=
n |
|
|
|
|
|
∑уi |
xi . |
|
|
|
|
i=1 |
Док-во. Пусть |
х и у произвольные |
из |
ЕП и { |
ei } произвольный |
|
|||||
|
|
n |
xi |
n |
уi . Но тогда (х,у)= |
ортонормированный |
в нем. Тогда х= ∑еi |
и у= ∑еi |
|||
|
|
i=1 |
|
i=1 |
|
n |
n |
n |
|
|
( ∑еi xi |
, ∑еi |
уi )= ∑уi xi , ввиду ортогональности ei. |
|
|
i=1 |
i=1 |
i=1 |
|
|
|
Теперь |
легко выяснить смысл понятия |
‘координата’ |
|
|
|
|
|
n |
ортонормированном |
базисе. Возьмем произвольный |
х= ∑еi xi |
||
|
|
|
|
i=1 |
в
и
n
произвольный ei из базиса. Вычислим (х, ei) =( ∑еi xi , ei)=xi . Т.е. координата
i=1
– это произведение вектора х на базисный орт.
19
в
1.9.Линейные операторы и матрицы
Опред. Оператор А называют линейным оператором, если он подчиняется требованиям: а – аддитивности А(х1+х2)=А(х1)+А(х2) и б – однородности А(кх)=кА(х), где х1, х2 из ЛП и к – действительное.
Примером может служить производная. Вторым примером может служить матрица. В самом деле, пусть дан оператор А и вектор х из ЛП. Пусть в ЛП задан базис { ei }. Тогда воздействуем оператором А на элемент
n |
уi . Т.к. А по условию линеен, |
х. Получим новый вектор (элемент ) у= ∑еi |
|
i=1 |
|
тоон установит линейную же связь между координатами векторов х и у. Т.е. получаем соотношения
y |
= ∑ 1 j |
|
j , |
|
|
|
|||
|
|
|
n |
|
|
|
|
|
|
|
|
1 |
j=1 a x |
|
|
|
a12 |
||
|
|
n |
|
|
|
|
a11 |
||
y |
2 |
= ∑ |
2 j |
x |
j , |
. Или фактически у= |
a21 |
a22 |
|
|
|
j=1 a |
|
|
|
|
|||
....................... |
|
|
an2 |
||||||
|
yn |
n |
|
|
|
|
an1 |
||
|
= ∑anj xj |
|
|
|
|||||
|
|
|
j=1 |
|
|
|
|
|
|
a1n
a21 х. Это значит
ann
оператор А и матрица А – одно и то же. Такую матрицу называют матрицей отображения ЛП в себя.
Пример 1.8. Оператор зеркального отражения в оси.
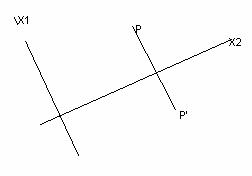
Определим его так: любая Р на плоскости α соответствует Р’ в той же плоскости так, что расстояние Р от прямой l равно расстоянию P’ от той же прямой; обе точки лежат на одном перпендикуляре к этой прямой, но по разные стороны от него.
Рис 1.1. Зеркальное отражение в оси.
Руководствуемся Рис 1.1. Пусть имеем базис е1 и е2 . Тогда легко получить соотношение между координатами точек (элементов пространства)
Р(х1,х2) и P’(у1,у2) :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
у1 |
= |
|
|
|
|
у1 =1х1 +0х2 , |
|
1 |
0 |
|
|
||
|
1 |
|
|
|
|
|
||||||||
|
у2 |
х |
|
Отсюда следует |
|
= 0х −1х |
|
, что дает у= |
|
|
|
х. |
||
|
=− |
х |
2 |
|
2 |
0 |
−1 |
|||||||
|
|
|
|
|
у2 |
1 |
|
|
|
|
|
|||
Матрицей |
(оператором) отражения |
в |
оси |
будет |
|
1 |
0 |
|
Ее |
|||||
матрица А= |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
−1 |
|
|
|
характерный признак – она симметрическая.
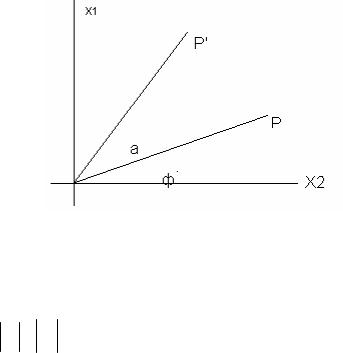
Пример 1.9. Оператор поворота плоскости на угол ф.
Определим его так: любая Р плоскости α переходит в Р’ в той же плоскости путем поворота вектора ОР на угол ф до совпадения векторов ОР и ОР’. Руководствуемся Рис 1.2. Пусть имеем базис е1 и е2 . Тогда легко получить соотношение между координатами точек (элементов пространства)
Р(х1,х2) и P’(у1,у2) , исходя из таких действий. Пусть ОР= |
|
х |
|
; х = |
|
х1 |
|
= |
|||||
|
|
||||||||||||
|
|
|
х2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
Cosф |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
= |
|
х |
|
|
|
|
|
|
|
||||
|
Sinф |
|
|
|
|
|
|
||||||
Рис 1.2. Поворот плоскости на угол ф.
|
|
у |
|
|
|
|
|
у |
|
Cos(α +ф) |
|
|
||
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда OP’=y= |
у2 |
|
= |
|
|
|
|
|
|
= |
|
|||
|
|
|
у |
|
Sin(α +ф) |
|
|
|||||||
|
|
|
|
|||||||||||
у |
|
(CosαCos |
|
|
|
|
|||
|
− SinαфSinф) |
И т.к. |
||
у |
|
(SinαCos |
|
|
|
||||
|
−CosαфSinф) |
|
х = y , то получаем окончательную связь между координатами векторов
|
|
= x1 Cosα − x2 Sinα, |
|
||||
y1 |
|
||||||
|
|
= 1 Sinα + |
|
2 Cosα . Т.е. |
оператором поворота будет матрица |
||
y |
|
x |
|||||
|
2 |
x |
|
|
|
|
|
поворота |
вида |
Cosα |
− Sinα |
- симметрическая, невырожденная с |
|||
|
|
|
|
||||
|
|
|
Sinα |
Cosα |
|
||
определителем, равным 1.
1.10.Задача о собственных значениях
Ограничимся в рассуждениях ЛП размерности 3, евклидовым, с ортонормированным базисом (е1 е2 е3). Договоримся вектором (элементом
21
→
ЛП) называть матрицу-столбец r = ( х1 х2 х3)T. Как уже известно, умножение квадратной матрицы А на вектор дает матрицу-столбец – новый вектор из того же ЛП.
→
Определение. Ненулевой r называют собственным вектором
→ →
оператора А (матрицы А), если выполняется равенство Аr =кr , где к –
некоторое действительное, которое называют собственным значением оператора А (матрицы А).
→ |
→ |
→ |
Равенство Аr |
=кr |
эквивалентно равенству (А-кЕ) r =0, которое |
после выполнения действий слева фактически будет иметь вид однородной системы линейных уравнений. Однородная система имеет ненулевые (нетривиальные) решения , только если ее определитель равен нулю. (См раздел 1.5). Получаем det(A-kE)=0 или для размерности 3
a11 − k |
a12 |
a13 |
|
|
a21 |
a22 − k |
a23 |
=0. |
(1.10.1) |
a31 |
a32 |
a3 − k |
|
|
Последнее уравнение с неизвестным к называют характеристическим уравнением (в`ековым). Решив уравнение (1.10.1) мы получим собственные значения оператора А (матрицы А). Теперь поступаем так. Берем первое
→
собственное значение и подставляем его в систему (А-кЕ) r =0 с
→
неизвестными координатами вектора r . Определителем этой системы будет определитель из леовй части уравнения (1.10.1) при заданном к. Решаем эту систему по известному алгоритмы из раздела 1.5. Получаем координаты первого собственного вектора. Далее процесс повторяется для оставшихся собственных значений.
Пример 1.10. Найдите собственные значения и собственные векторы
|
5 |
2 |
−3 |
|
|
4 5 |
|
. Решение. Уравнение (1.10.1) имеет вид |
|
оператора (матрицы) А= |
− 4 |
|||
|
|
4 |
|
|
6 |
− 4 |
|
||
5 |
− к |
2 |
−3 |
|
|
|
|
4 |
5 − к |
− |
4 |
|
=0. Или к3-6к2+11к-6=0. Его решения (корни): к1=1; к2=2; |
|
|
|||||
|
6 |
4 |
− 4 |
− |
|
|
|
к |
|
||||
к3=3. Берем к1=1 и составляем систему |
с неизвестными координатами |
|||
→ |
|
4 x1 + 2 x1 −3 x1 = 0, |
||
первого собственного вектора r 1. Получаем систему |
|
4 x1 |
+ 4 x1 − 4 x1 = 0 . По |
|
|
|
|
6 x1 |
+ 4 x1 −5 x1 = 0 |
|
|
|
||
алгоритму раздела 1.5 ранг матрицы этой системы не меньше 1 (т.к. есть элементы , не равные нулю) и не больше 3 (т.к. определитель системы это левая часть характеристического уравнения). И потому rancA=2. Легко
