24
→
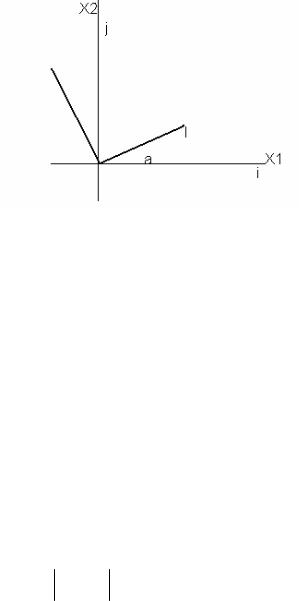
Мы имеем r = х1i+х2j = х’1I+х’2J . Но I и J тоже векторы, правда единичной длины. И потому I=iCosα +jCos(90-α ), J= iCosα +jCos(90+α ).
Или после подстановки полученного вместо координат х’1,х’2 получим
связь между старыми и новыми координатами |
|
х1 |
= |
Сosα |
− Sinα |
( х’1 |
|
|
|
|
|||
|
|
х2 |
|
Sinα |
Сosα |
|
х’2)T, которая соответствует матрице поворота плоскости на некоторый угол.
2.Векторная алгебра
Вэтом разделе рассматриваются основные действия с векторами, изучаемыми в курсе математики технического ВУЗа и применяемыми в
специальных дисциплинах.
2.1.Линейные операции над векторами
(Обзор и дополнения)
Определение. Вектором в математике принято называть направленный отрезок.
→ →
Обозначают вектор либо a , либо AB , если использовать его начало А
и конец В (порядок букв в записи не нарушать).
Вектор характеризуют направлением и длиной (модулем). Последний
→
обозначают AB или просто АВ.
В приложениях векторной алгебры используют три вида векторов: сободные (только они изучаются в данном разделе), которые остаются неизменными при параллельном переносе; скользящие (физика), которые
можно перемещать только вдоль их линии приложения и связанные (теоретическая механика), которые рассматривают только для точки их приложения.
→ →
Для свободных справедливо AB =CD , если точки А и С совпадают как и точки В и D. Фактически, это – определение равных
векторов.(действие, операция равенства).
25
Договоримся (определим) называть суммой двух векторов вектор, соединяющий начало одного слагаемого с концом второго, при условии, что
начало второго совпадает с концом первого(правило треугольника). Можно определить сумму векторов по правилу параллелограмма.
Первое определение оказывается более удобным при суммировании большого числа векторов. Оно же удобно при построении векторных диаграмм при расчете электрических цепей переменного тока.
Противоположными будем называть векторы, совпадающие своими концами , но направленные в разные стороны.
Если векторы расположены параллельно одной прямой, то их называют коллинеарными.
→
Произведением вектора a на константу с называют вектор, модуль
|
|
|
→ |
|
→ |
которого равен с |
а |
и который коллинеарен вектору a . При этом при |
|||
|
|
|
|
→ |
→ |
положительном с направления a |
и сa совпадают, при отрицательном – |
||||
|
|
|
|
направления противоположны. |
|
|
Определение. Линейной комбинацией векторов называют выражение |
||||
n |
→ |
→ |
→ |
→ |
→ |
∑αi ai =α1 ai +α2 |
a |
2 +α3 a3 +…+αn an . αi - некоторые действительные |
|||
i−1 |
|
|
|
|
|
константы. Это - обобщение линейных операций. Определение. Векторы называют линейно-независимыми, если их
линейная комбинация равна нулю тогда и только тогда, когда все коэффициенты αi линейной комбинации равны нулю.
В противном случае векторы называют линейно-зависимыми. В этом случае один из них можно представить линейной комбинацией остальных,
→ |
→ |
→ |
→ |
т.к. уравнение α1 ai +α2 |
a2 +α3 |
a3 +…+αn an =0 оказывается разрешимым |
|
относительно вектора, перед которым записан ненулевой коэффициент. Определение. Множество линейно-независимых ненулевых векторов
называют векторным базисом.
В этом случае имеется возможность любой вектор, который не входит в базис представить линейной комбинацией базисных векторов.
Коэффициенты такой линейной комбинации называют координатами вектора в данном базисе. Для пространства и плоскости такое действие в физике называют разложением вектора по направлениям составляющих векторов. В математике – разложением по базису (в базисе) Рис 2.1.
26
|
|
|
|
|
|
|
|
|
|
→ |
|
|
→ |
→ |
|
|
|
|
|
|
|
|
|
|
Рис 2.1. Разложение вектора a в базисе ai |
иa2 . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
→ |
|
|
|
|
|
Если анализировать разложение на Рис 2.1, то видно, что ОA=α1 |
ai , а |
|||||||||
|
→ |
|
|
|
→ |
|
|
|
|
|
|
||||
ОВ |
=α2 a2 из условия коллинеарности. И тогда по правилу параллелограмма |
||||||||||||||
|
|
|
|
|
|
|
|
|
→ → |
→ |
→ |
→ |
|
|
|
|
|
|
при суммировании получаем a =ОA+ОВ=α1 |
ai +α2 |
a2 - о чем и было |
||||||||||
|
|
|
|
|
|
|
|
|
сказано выше. |
|
|
|
|
|
|
|
|
|
|
|
Наиболее простым и широко распространенным является декартов |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
→ |
→ |
→ |
|
|
|
|
|
|
базис – три взаимно перпендикулярных вектора i , |
j |
, k , такие что |
|
||||||||
|
→ |
|
|
→ |
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
i |
|
= |
j |
= |
|
k |
|
=1. Если с этими векторами связать соответственно координатные |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оси Ох,Оу,Oz и расположить их общее начало в точке О, то и будет получен декартов базис. Это очень удобно, т.к. термин “координаты векторa” в таком базисе совпадает с термином “координаты точки”. Следует быть осторожным в использовании этих терминов, т.к. оба они полностью
→
совпадают только для радиуса-вектора r , начало которого всегда в точке О. В новых терминах запишем обозначение вектора в декартовом базисе
→ →
a =ax i +ay
→ →
j +az k . Или в компактном виде
→
a ( ax;ay;az)
Используя разложение вектора в декартовом базисе (далее будем говорить – координатную форму вектора или просто координаты вектора), найдем модуль вектора как диагональ прямоугольного параллелепипеда
→
а= a2x + a2y + a2z . А, используя действие умножения вектора на
→
действительное число, получим единичный вектор направления вектора a .
|
|
→ |
→ |
|
1 |
|
|
Его обозначим aо . И он равен aо |
= 2 |
|
|||
|
2 |
2 |
||||
|
|
|
|
ax |
+ ay |
+ az |
→ → |
→ → |
→ |
→ |
|
|
|
(ax i +ay j +az k )= i Cosα + j Cos β |
+ k Cos γ . Координаты единичного |
|||||
27
вектора называют направляющими косинусами. Направляющие косинусы обладают важным свойством
Cos2 α +Cos2 β +Cos2 γ =1, т.к. сумма слева есть длина единичного вектора. Это свойство обобщает известное основное тригонометрическое
тождество.
Отметим попутно важное практическое правило – линейные операции, выполняемые над векторами, эквивалентны тем же операциям, выполненным
над соответствующими координатами векторов.
Это правило удобно применять, если возникает вопрос о том, будет ли данный набор векторов образовывать базис, а также при разложении вектора,
заданного в декартовом базисе по произвольному базису из векторов, заданных своими декартовыми координатами.
2.2.Скалярное произведение векторов
Термином (билинейные операции над векторами) иногда называют операции скалярного и векторного произведений двух векторов.
|
|
|
|
|
|
|
→ |
→ |
Определение. Скалярным |
произведением |
двух |
векторов a |
и b |
||||
|
→ |
|
→ |
|
|
|
|
|
называют величину |
а |
|
b |
Cosф |
, где ф – |
угол |
между векторами. |
|
→ → |
|
|
→ → |
|
|
|
|
|
Обозначения a b или ( a ,b). |
|
|
|
|
||||
По этому определению двум векторам ставится в соответствие скаляр, который можно истолковать как работу постоянной по величине и направлению силы на прямолинейном участке пути.
Из определения вытекают простейшие свойства такого произведения.
→ → → → |
→ → |
→ → |
→ → → → → → → |
→ |
1. a b=b a ; |
2. С( a b)=(Сa ) b. |
3. ( a +b)с = a с+b с |
и 4. a |
|
→
b=0
для ненулевых векторов, если векторы ортогональны (перпендикулярны). Можно получить формулу для вычисления скалярного произведения,
если векторы заданы в координатной форме (своими координатами). Пусть
→ → → |
→ |
→ |
→ |
→ |
→ |
→ → |
a =ax i +ay j +az k |
и b=bx i +by j +bz k |
. Тогда a b= ax bx +ay by +az bz. Т.к. при |
||||
перемножении по свойству 3 с учетом определения остальные слагаемые будут равны нулю.
→ → |
→ |
2 .Читается – |
Из последнего соотношения следует, что a a = |
а |
|
скалярный квадрат равен квадрату модуля. |
|
|
28
Из определения и полученных соотношений вытекают другие формулы. Например, для проекции одного вектора на другой получаем
→ →
→ |
|
прa→ a = a→b . Условие перпендикулярности векторов axbx+ayby+azbz=0. |
|
b |
|
2.3.Векторное произведение векторов |
|
→ |
→ |
Определение. Векторным произведением двух векторов a |
и b называют |
→
вектор ñ , который:
-имеет модуль, равный произведению модулей перемножаемых векторов на
|
|
→ |
|
→ |
|
→ |
|
|
|
синус угла меду ними - |
ñ |
= |
a |
|
b |
sinф; |
|
|
|
|
|
|
|
|
|
|
→ |
→ |
|
-ортогонален (перпендикулярен) каждому из векторов a и b (т.е. плоскости |
|||||||||
|
→ |
→ |
|
|
|||||
с векторами a и b); |
|
|
|||||||
→ → |
→ |
→ → |
|
|
|||||
-вместе с векторами a и b в порядке a , |
b,ñ образует правую тройку |
||||||||
|
|
|
|
|
|
|
r |
→ |
→ |
векторов. Обозначают векторное произведение a ×b или [ a |
, b]. |
||||||||
|
|
|
|
|
|
|
|
→ |
→ → |
Комментарий. Классическое понятие правой тройки векторов a , b,ñ в указанном порядке: если наблюдать с конца любого вектора поворот от
следующего за ним к предыдущему в направлении против часовой стрелки, то тройка векторов правая. В противном случае – левая.
→ →
Примером правой тройки будет набор декартовых базисных векторов i , j ,
→
k . А в бытовом понятии правую тройку связывают с правым буравчиком
(правой резьбой), когда при вращении по часовой стрелке буравчик (винт, гайка) продвигается вглубь от вращающего.
→ →
Т.к. a b sinф, то геометрически определение говорит о том, что площадь
→ →
параллелограмма, построенного на множителях a и b равна модулю вектора
→
ñ.
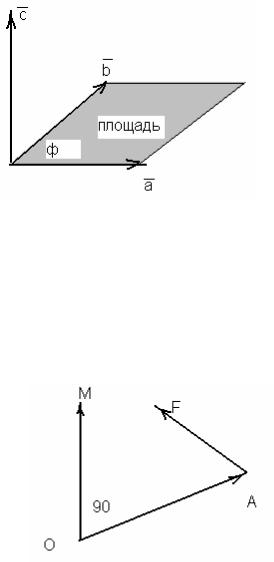
29
К определению a ×br
В качестве механической интерпретации векторного произведения
→ |
→ |
может быть взят момент М силы |
F (постоянной по величине и |
→
направлению), приложенной к точке А относительно точки О. Вектор М направлен так, что образует правую тройку с перемножаемыми векторами и
|
→ |
|
→ |
|
численно равен величине |
ОА |
|
F |
Sinф. |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
Механическая интерпретация a ×b . |
|
|
|
||||||||
|
|
Справедливы следующие свойства векторного произведения. |
||||||||||||||
|
|
С1.Для коллинеарных векторов |
→ |
→ |
|
|
|
r |
r |
|||||||
|
|
a |
и |
справедливо a ×b =0. |
||||||||||||
|
|
|
|
|
|
|
|
r |
r |
r br |
r |
|
|
|
||
|
|
|
|
|
|
С2. (a +b)×c = a ×c +b ×c . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
С3. a ×(λb) =λ(a ×b ). |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
→ |
→ |
→ |
→ |
|
Координатная форма вычисления a ×b . Пусть a =ax i +ay j |
+az k и |
||||||||||||||
→ |
→ |
→ |
→ |
|
|
r |
→ |
→ |
|
→ |
|
→ |
→ |
→ |
|
|
b=bx i +by |
j +bz k . Тогда a ×b =(ax i +ay j +az k )х(bx i +by |
j +bz k ). Далее |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
→ |
→ |
→ |
|
|
|
используем взаимное расположение векторов i , |
j |
, k и свойство 3 получим |
||||||||||||||
|
|
|
|
|
|
|
по определению |
|
|
|
|
|
||||
|
|
|
→ → |
→ |
→ |
→ → |
|
→ → |
|
→ → |
→ |
→ |
||||
|
|
axbx i |
хi +aybx j хi |
+azbx k |
хi +aхbу i х j |
+aуby j х j +azbуk х j + |
||||||||||
|
|
→ |
→ |
→ |
→ |
→ |
→ |
|
|
|
|
→ |
|
→ |
||
|
+axbz i |
хk +ay bz |
j хk |
+az bz k |
хk = (aхbу-aybx) k +( azbx- axbz) j + |
|||||||||||
|
|
|
30 |
|
|
→ |
→ |
→ |
|
|
|
|||
→ |
i |
j |
k |
|
+( ay bz - azbу) i = |
ax |
ay |
az |
. Полученная символическая формула не |
|
bx |
by |
bz |
|
|
|
|
|
|
противоречит ни свойствам определителя о смене знака при смене местами параллельных рядов, ни свойству векторного произведения о смене знака при смене порядка множителей. Из нее получается простое правило проверки
коллинеарности векторов – равенство отношений ax = ay = az (или |
||||
|
|
bx |
by |
bz |
|
|
пропорциональность координат). |
|
|
|
|
2.4.Смешанное произведение векторов |
|
|
|
|
Рассмотрим произведения трех векторов : |
|
|
→ |
→ |
→ |
|
|
(( a |
,b), с) – уже известное нам произведение скаляра на вектор – и |
|||
|
|
потому ничего нового; |
|
|
→ |
→ |
→ |
|
|
[[ a |
,b],с] - двойное векторное произведение, которое имеет узкое |
|||
|
|
приложение в механике; |
|
|
→ |
→ |
→ |
|
|
([ a |
,b],с) – векторно-скалярное (смешанное) произведение, которое |
|||
имеет широкое применение в математике и приложениях.
→ →
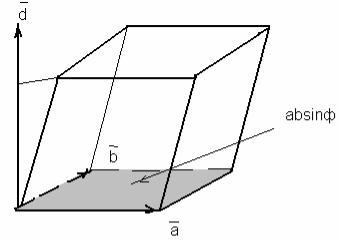
Анализируя известное произведение [ a ,b] по Рис.2.2, можно получить геометрическую интерпретацию для смешанного произведения
|
|
|
|
→ |
→ |
→ |
|
|
|
|
|
|
|
|
([ a |
,b],с). Модуль векторного произведения – площадь |
|||||
|
|
|
|
параллелограмма, построенного на векторах-множителях и равной |
||||||
|
→ |
|
|
r r |
|
|
|
|
→ |
→ |
|
|
|
|
|
|
|||||
|
d |
|
|
= a ×b . Если теперь перемножить скалярно векторы d |
и с, то получим |
|||||
|
|
отрезок ОВ, равный высоте параллелепипеда, построенного на векторах- |
||||||||
|
|
|
|
|
→ |
→ |
→ |
→ |
→ |
→ |
|
|
|
|
сомножителях a |
,b |
,с |
как на ребрах. Т.о., модуль ([ a |
,b],с) численно |
||
равен объему параллелепипеда, построенного на векторах множителях.
→ → →
К определению ([ a ,b],с)
31
Используя координатную форму векторного произведения, получаем координатную форму смешанного произведения
|
→ |
→ |
→ |
→ → → |
i |
j |
k |
([ a ,b],с)= |
ax |
ay |
az |
|
bx |
by |
bz |
|
|
|
|
→ → → → →
( сx i +сy j +сz k )=(( aхbу - aybx ) k +( azbx- axbz) j +( ay
|
|
→ |
|
→ → |
→ |
bz - azbу) i ) ) ( сx i +сy j +сz k )=( aхbу - aybx ) сx +( azbx- axbz) сy +( ay bz - azbу) сz |
|||||
|
сx |
сy |
сz |
|
|
= = |
ax |
ay |
az |
. Если в последнем определителе переставим местами 1-ю и 3- |
|
|
bx |
by |
bz |
|
|
ю строки, то определитель не изменится и мы получим более удобную запись координат перемножаемых векторов в порядке их следования в произведении.
Из последней формулы для вычисления смешанного произведения следует возможность проверки компланарности (параллельности одной
→ → →
плоскости) трех векторов – если ([ a ,b],с)=0, то векторы-множители компланарны. И следствием последнего равенства будет условие линейной зависимости трех векторов в пространстве .
2.5.Типовые задачи, решаемые средствами векторной алгебры
Деление отрезка в данном отношении k.
Определение. Пусть дан отрезок АВ и точка М на нем или его продолжении. Говорят, сто М делит АВ в отношении к, если k= ±АМ/MB.
→ |
→ |
|
При этом знак + берут, если векторы АМ и |
МВ сонаправлены и знак --, |
|
если противоположно направлены. |
|
|
|
→ |
→ |
Решение задачи. Из определения следует соотношение АМ =кМВ.
Но точно таким же соотношением связаны соответствующие координаты
xM − xA =
указанных векторов. Получаем y − y =zMM − zAA =
k(xB − xM )
k( yB − yM ) из которой следуют k(zB − zM )
формулы для вычисления координат делящей точки хМ = хА + к хВ и т.д.
1+ к
→
Получение единичного вектора данного направления a . Дан вектор
→
a (ах, ау, az) – своими координатами. Найти вектор единичной длины и того
же направления.
Решение. Интересующий нас вектор равен