14 Векторний та мішаний добутки двох векторів

a = {x1; y1; z1} і b = {x2; y2; z2} в декартовій системі координат - це вектор значення якого можна знайти за наступними формулами:

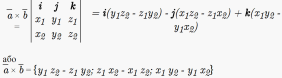
Властивість 1. Модуль векторного добутку двох векторів a і b дорівнює площині паралелограма побудованого на цих векторах.

Властивість 2. Якщо векторний добуток двох векторів a и b дорівнює нулю то вектори колінеарні.

Мішаний добуток векторів 

Визначення. Скалярний добуток вектора на векторний добуток векторівіназивається мішаним добутком векторів,,.

Отже, мішаним добутком векторів ,іє виразі представляє собою, очевидно, скаляр.

З‘ясуємо геометричний зміст введеного поняття. Нехай точка О є загальний початок трьох некомпланарних векторів ,,.

Побудуємо на заданих векторах паралелепіпед (рис.13) і знайдемо вектор . Із визначення скалярного добутку векторів, отримаємо

Але оскільки вектор перпендикулярний площині векторіві, то проекція векторана вісь, направлену по вектору, або дорівнює висоті паралелепіпеда, якщо ця проекція додатна (тобто, якщо вектори,,утворюють праву трійку), або дорівнює висоті, взятій зі знаком мінус, якщо ця проекція від‘ємна (тобто, якщо три заданих вектора утворюють ліву трійку).

Отже, мішаний добуток трьох векторів дорівнює об‘єму паралелепіпеда, побудованого на цих векторах, якщо вони утворюють праву трійку, і дорівнює об‘єму паралелепіпеда, взятому зі знаком мінус, якщо вектори утворюють ліву трійку.

Якщо у вибраній трійці їх переставити, то паралелепіпед, побудований на цих векторах, очевидно, не зміниться. Зокрема, не зміниться і абсолютна величина мішаного добутку. Легко відмітити, що при круговій перестановці векторів права трійка векторів залишається правою, а ліва лівою. Тому при круговій перестановці векторів мішаний добуток векторів не змінюється.

Отже,

Якщо вектори задані своїми координатами в ортонормованому базисі ,,:

,

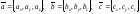Якщо задані три вектора компланарні, то їх мішаний добуток, очевидно, дорівнює нулю. Навпаки, якщо мішаний добуток трьох векторів дорівнює нулю, то ці вектори обов’язково компланарні. Дійсно, якщо скалярний добуток векторів ідорівнює нулю, то векторперпендикулярний вектору; алеперпендикулярний також площині векторіві. Таким чином векторлежить в площині векторіві. Звідси, вектори,,компланарні.

Отже, рівність нулю мішаного добутку трьох векторів є необхідна і достатня умова їх компланарності.

Формулу (2) можна записати, використовуючи визначник третього порядку

Властивість 1. Модуль мішаного добутку трьох векторів дорівнює об'єму паралелепіпеда, утвореного цими векторами.

Властивість 2. a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]

Властивість 3. Якщо мішаний добуток трьох не нульових векторів дорівнює нулю, то ці вектори компланарні.

1. Похідна функції

Похідною функції y = f(x) у точці Х називають число, до якого прямує відношення

Фізичний зміст похідної. Якщо матеріальна точка рухається прямолінійно і її координата змінюється за законом S = S(t), то швидкість її руху v(t) у момент t дорівнює похідній S'(t):

v(t) = S'(t).

Геометричний зміст похідної: значення похідної функції y = f(x) у точці x₀ дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x₀: y' = f'(x₀) = k = tgα.

Рівняння дотичної до графіка функції y = ƒ(x) має вигляд y - y₀ = ƒ ′ (x₀)(x-x₀)

де (x₀; y₀) — точка дотику.

Пряма, яка проходить через точку дотику дотичної, наз. нормальною до графіку функцii в цій точці.

2. Властивості похідних

Сталої (C)' = 0,

добутку функції на сталу (c•u)' = c•u',

алгебраїчної суми кількох функцій (u ± v)' = u' ± v',

добутку двох функцій (u•v)' = u'v + uv',

частки двох функцій ,

складної функції

оберненої функції ,

параметрично заданої функції

неявної функцiї Якщо залежність між та задана в неявній формі , причому надалі будемо вважати, що диференційовна функція, то для знаходження похідної достатньо:

а) знайти похідну по від лівої частини рівняння,, враховуючи, що є функцією;

б) прирівняти цю похідну до нуля ;

в) розв’язати отримане рівняння відносно 

3. Похідна елементарних функцій

4. Правило Лопіталя

Правило Лопіталя (розкриття невизначеності за умови .

Якщо:

1) функції ідиференційовні на інтервалі,для всіх;

2) ;

3) існує скінченна або нескінченна границя ,

то існує границя , причому має місце рівність:

.       

6. Похідні вищих порядків

Означення: Похідна від похідної першого порядку, тобто , називається похідною другого порядку або другою похідною функціїі позначається,,,. Отже,або.

Якщо на існує, яка, в свою чергу, є диференційовною на, то похідна третього порядку функціїнацетак далі. Похідна-го порядку функціїна.

Означення: Функція, яка має похідну -го порядкуна(-у похідну) називаєтьсяраз диференційовною на. Якщо ж-а похіднає ще й неперервною на, то функціяназиваєтьсяраз неперервно диференційовною на.

У загальному випадку для обчислення похідної вищого порядку потрібно знайти спочатку похідні всіх нижчих порядків. В окремих випадках вдається встановити загальний вираз для похідної -го порядку.

5. Диференціал функції

Означення: Якщо функція  має похідну  в точці , то вираз  називається диференціалом функції в цій точці і позначається символом . Тобто, .                       

Зауваження: Диференціал функції  в даній точці є головною лінійною частиною приросту функції, пропорційною приросту аргументу з коефіцієнтом пропорційності :

.

Диференціал незалежної змінної ототожнюється з її приростом, тобто

.

Для будь-якої диференційовної в точці х функції  формулу можна записати так:

. Звідки отримаємо, що          

тобто похідну можна розглядати як відношення двох диференціалів.

Правила знаходження диференціала

З правил знаходження похідної випливають правила знаходження диференціала. Якщо функції ,   -диференційовні в точці х, то

1) .

2) .

Зауваження. , де .

 

3) , .

Геометричний зміст диференціала 

Нехай ,  та існує . За означенням диференціала .

Скористаємося геометричним змістом похідної: .

Зтрикутника   маємо:   або . Але , тому .

Отже, диференціал функції  в точці  визначає приріст ординати дотичної до кривої в точці  при переході від абсциси  до абсциси      

Застосування диференціала в наближених обчисленнях

З означення похідної функції в точці  випливає, що її приріст  можна подати у вигляді: , де , якщо .

Отже, при малих  має місце наближена рівність:

, тобто .

Звідки

. (3.12)

Формула (3.12) дозволяє знаходити значення функції  в точці , якщо відомі значення  і , з точністю 

 

,

де .

Диференціювання функцій, заданих параметрично

Нехай функції  і  параметрично задають функцію , причому  і  -функції диференційовні за змінною t і .

Похідну  від функції y за змінною x знаходимо, диференціюючи  і  за змінною t

, .

Тоді

,

тобто

.                      

6. Монотонність функцiї та її локальні екстремуми.

Зростання і спадання функцій

Нагадаємо, що функція називається зростаючою (спадною) на інтервалі, якщо для довільних, якщовиконується нерівність.

Теорема: (достатня умова монотонності). Припустимо, що функція диферен­ційовна на. Якщодля всіх, то– зростаюча на; якщодля всіх, то– спадна на.

Зауваження.Якщо на, тостала на.. Якщо дотичні до кривої на деякому проміжку спрямовані під гострими кутами до осі абсцис , то функція зростає, якщо під тупими, то спадає.

Екстремум функції

Означення: Точка називається точкою максимуму функції, якщо в деякому околі точкивиконується нерівність.

Означення: Точка називається точкою мінімуму функції, якщо в деякому околі точкисправджується нерівність

Точки максимуму і мінімуму називаються точками екстремуму функції, а значення функції у точках і – відповідно максимумом і мінімумом функції. Максимум і мінімум функції об’єднуються під загальною назвою екстремуму функції, який часто називають локальним екстремумом, підкреслюючи, що поняття екстремуму пов’язане з достатньо малим околом точки екстремуму. Це означає на одному проміжку функція може мати декілька точок максимуму і мінімуму.

Теорема: (необхідна умова екстремуму). Якщо функція має в точціекстремум, то її похідна в цій точці дорівнює нулевіабо не існує

Іншими словами, функція може мати екстремум тільки у тих точках, в яких похідна дорівнює нулеві або не існує. Точки, в яких похідна функції дорівнює нулеві або не існує, називаються критичними (або стаціонарними) точками. Звертаємо увагу на те, що ці точки повинні входити в область визначення функції. Однак легко переконатись, що критична точка зовсім не обов’язково є точкою екстремуму.

Теорема: (перша достатня умова екстремуму). Якщо, переходячи через точку , похідна диференційовної функціїзмінює знак з плюса на мінус, то точкає точкою максимуму функції, а якщо з мінуса на плюс, то– точка мінімуму.

9. Загальна схема дослідження функцій  і побудова їх графіків

Досліджувати функцію рекомен­дується за такою схемою: 1. Знайти область визначення функції. 2.Дослідити функцію на парність– непарність,

3.Дослідити на періодичність,

4. Встановити точки перетину графіка з осями координат та інтервали знакосталості функції.(з Ох та Оу) 5. Знайти вертикальні та похилі асимптоти графіка функції. 6. Визначити екстремуми та інтервали монотонності функції. 7. Знайти інтервали опуклості і увігнутості функції та точки перегину.

8. побудувати графік.

6. Опуклість та вгнутість кривих; точки перегину; асимптоти кривої.

Означення:  Функція називається опуклою (опуклою вгору) на інтервалі, якщо для довільних двох точокз цього проміжку відрізок, що з’єднує точкиі, розміщений під графіком цієї функції(рис. 7).

Означення: Функція називається увігнутою (опуклою вниз) на інтервалі, якщо для довільних двох точокз цього проміжку відрізок, що з’єднує точкиі, розташований над графіком цієї функції(рис. 8).

Рис. 7.Опукла функція     Рис. 8. Увігнута функція

Теорема: (достатня умова опуклості та увігнутості функції). Нехай функція двічі диференційовна на інтервалі. Тоді: 1)якщо на, то функція увігнута на цьому інтервалі; 2) якщо на, то функція опукла на цьому інтервалі. Означення: Точкою перегину графіка неперервної функції називається точка, яка відокремлює інтервали, на яких функція опукла і увігнута.

Теорема: (ознака точки перегину). Якщо і, переходячи через точку, змінює знак, тоє точкою перегину графіка функції.

Асимптоти графіка функції

Досі ми розглядали характерні точки графіка функції: точки екстремуму, точки перегину. Тепер розглянемо характерні лінії.

Означення: Асимптотою графіка функції називається пряма, яка має таку властивість: відстань від точкидо цієї прямої стає як завгодно малою за необмеженого віддалення точки графіка від початку координат.

Розрізняють вертикальні (рис. 10, а) та похилі (зокрема горизонтальні) (рис. 10, б, в) асимптоти. а) вертикальна асимптота; б) похила асимптота;  в) горизонтальна асимптота

Рис. 10. Асимптоти графіка функції

Визначення асимптот графіка функції ґрунтується на таких твердженнях.

Теорема: Пряма є вертикальною асимптотою графіка функції, якщоабо.

Наприклад, графік функції має вертикальні асимптоти. Теорема:Якщо існують скінченні границі і, тоє похилою асимптотою графіка функції.

Якщо обидві границі скінченні лише коли , то прямає відповідно тільки правосторонньою (лівосторонньою) похилою асимптотою графіка функції.

Схема дослідження функції на екстремум. 1. Знайти область визначення функції. 2. Обчислити похідну. 3. Визначити критичні точки функції, тобто точки, в якихабо не існує. 4. Дослідити знак похідної ліворуч і праворуч від кожної критичної точки і зробити висновок про наявність екстремумів функції. 5. Знайти екстремуми функції, обчисливши значення функції в точках екстремуму.

Теорема:(друга достатня умова екстремуму). Якщо функція двічі диференційовна і, а, тоє точкою мінімуму функції; якщо, тоє точкою максимуму.

Схема дослідження на екстремум функції за допомогою другої достатньої умови загалом аналогічна до наведеної вище схеми. Відмінність в п. 4, який встановлює наявність екстремуму: тут необхідно знайти другу похіднуі визначити її знак у кожній критичній точці.