17) Бесконечно малые величины

Функция называетсябесконечно малой функцией (б.м.ф.) при (или в точке), если

Основные свойства бесконечно малых функций

1°   Сумма конечного числа б.м функций является функцией б.м.

2°   Произведение б.м функции на ограниченную есть функция б.м.

3°   Произведение двух б.м функций есть функция б.м.

4°   Произведение б.м функции на константу является б.м функцией.

5°   Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.

6°   Функция , обратная к б.м функции, есть функция бесконечно большая. Верно и обратное.

18)Бесконечно большие величины

Функция называется бесконечно большой, если при х→а.

Бесконечно большая величина предела не имеет

Переменная, принимающая значения, обратные по величине соответственным значениям бесконечно большой величины, есть величина бесконечно малая. Хотя в некоторых источниках и применяются условные записи = 0 и=

Если A постоянная величина, не равная нулю, то произведение A на бесконечно большую величину есть величина бесконечно большая.

Произведение двух бесконечно больших величин есть величина бесконечно большая.

Отношение бесконечно большой величины к бесконечно малой есть величина бесконечно большая.

Сумма двух бесконечно больших величин одинакового знака есть бесконечно большая величина того же знака.

Отношение двух бесконечно больших величин не обязательно есть бесконечно большая величина.

19) Первый замечательный предел

Первый замечательный предел:

Следствия из первого замечательного предела

1°  

2°  

3°  

4°  

20) Второй замечательный предел

Второй замечательный предел:

Следствия из второго замечательного предела :

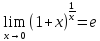
, x→0

а^х-1~хlna, x→0

e^х-1~х, x→0

(1+x)^α-1~xα, x→0

22) Неперервність функції

Функцію f (x) називають неперервною в т. x0 , якщо вона визначена в цій точціі деякому її околі і . тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції

1) вона визначена в цій точці і в деякому її околі;

2) нескінченно малому приростові аргументу відповідає нескінченно малий приріст функції:

, або .

3)існує границя 

4)..

Точка розриву - це така точка (значення аргументу) в якій функція не є неперервною.

Розрізняють такі види точок розриву:

Розрив називають усувним, якщо в даній точці існує границя функції, що не збігається з значенням функції.

Точку називають точкою розриву першого роду, якщо існують скінченні ліва та права границі в даній точці, та вони не збігаються.

Якщо хоча б одна одностороння границя не існує, чи нескінченна, то точку називають точкою розриву другого роду.

21) Розкриття невизначеностей

Розкриття невизначеностей - методи обчислення межфункцій, заданих формулами, які в результаті формальної підстановки в них граничних значень аргументу втрачають сенс, тобто переходять у вирази типу:

по яких неможливо судити про те, чи існують чи ні шукані межі, не кажучи вже про знаходження їх значень, якщо вони існують.

Найпотужнішим методом є правило Лопіталя, однак і воно не у всіх випадках дозволяє обчислити межа. До того ж прямо воно застосовується лише до другого і третього з перерахованих видів невизначеностей, тобто відносин, і щоб розкрити інші типи, їх треба спочатку привести до одного з цих.

Також для обчислення меж часто використовується розкладання висловів.

Для розкриття невизначеностей видів  ,  користуються наступним прийомом: знаходятьмежа(натурального)логарифмависловлювання, що містить дану невизначеність. У результаті вид невизначеності змінюється. Після знаходженнямежівід нього берутьекспоненту.

Для розкриття невизначеностей типу використовується наступний алгоритм:

Виявлення старшого ступеня змінної;

Поділ на цю змінну як чисельника, так і знаменника.

Для розкриття невизначеностей типу існує наступний алгоритм:

Розкладання на множники чисельника і знаменника;

Скорочення дробу.

Для розкриття невизначеностей типу іноді зручно застосувати наступне перетворення:

Нехай і(типа воспользоватся бесконечно большими величинами)

Таблиця 2 Основні типи рівнянь прямої лінії на площині

№ з/п	Рівняння прямої лінії	Аналітичний вигляд рівняння прямої лінії	Параметри рівняння прямої лінії	Зв'язок між пара-метрами рівняння прямої лінії
1	Загальне рівняння прямої
2	Рівняння прямої "у відрізках"
3	Рівняння прямої з кутовим коефіцієнтом
4	Канонічне рівняння прямої
5	Параметричне рівняння прямої
6	Рівняння прямої, що проходить через дві точки

Неповні рівняння прямої лінії на площині

№ з/п	Коефіцієнти рівняння	Рівняння прямої	Розташування прямої на площині
1			Проходить через початок координат
2			Паралельна до осі
3			Паралельна до осі
4			Координатна вісь
5			Координатна вісь

Таблиця 3 Взаємне розташування прямих ліній на площині

Прямі, задані рівняннями: ,
1	Умова паралельності:
2	Прямі збігаються:
3	Умова перпендикулярності:
4	Кут між прямими:
5	Точка перетину
Прямі, задані рівняннями: , .
6	Умова паралельності:
7	Умова перпендикулярності:
8	Кут між прямими:
Прямі, задані рівняннями:,  ,
9	Умова паралельності:
10 Умова перпендикулярності:
11 Кут між прямими:
12 Точка перетину прямих

Таблица эквивалентных б.м. функций при

Таблиця похідних функції