
- •Министерство образования, науки и молодежи республики крым гбпоу рк «керченский политехнический колледж»
- •Методические рекомендации
- •Методические рекомендации:
- •Тематический план
- •Раздел 2. Линейная алгебра
- •Раздел 3. Основы математического анализа
- •Раздел 4. Основы интегрального и дифференциального исчисления
- •Раздел 6. Дифференциальные уравнения
- •Раздел 8. Элементы теории вероятностей и математической статистики
- •Числовые характеристики выборки.
- •Раздел 3. Основы математического анализа
- •1.Числовые ряды
- •2. Ряды с положительными членами.
- •3. Знакопеременные ряды
- •4. Степенные ряды
- •5. Ряд тейлора
- •Задания контрольной работы Комплексные числа
- •Линейная алгебра.
- •Основы математического анализа Основы интегрального и дифференциального исчисления
- •Дифференциальные уравнения
- •Элементы теории вероятностей и математической статистики
- •Рекомендованная литература
- •Интернет-ресурсы:
3. Знакопеременные ряды
Числовой ряд, содержащий как положительные так и отрицательные члены, называется знакопеременным.
12. Пусть ряд
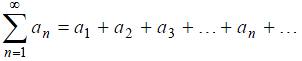 (8)
(8)
является знакопеременным. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
 (9)
(9)
Если ряд (9) сходится, то и ряд (8) тоже сходится. Ряд (8) при этом называется абсолютно сходящимся.
13. Если ряд (9) расходится, то из этого не следует, что и (8) расходится, ряд (8) может оказаться как сходящимся, так и расходящимся.
Возможен случай, когда ряд (8) сходится, а (9) расходится. Тогда ряд (8) называется условно (неабсолютно) сходящимся.
14. Знакопеременный ряд вида
 называется
знакочередующимся.
называется
знакочередующимся.
Признак Лейбница. Если члены знакочередующегося ряда, начиная с некоторого номера N,
1)монотонно
убывают по абсолютной величине и
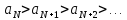 и
и
2) стремятся к нулю
![]() ,
,
то ряд сходится, сумма его положительна и не превышает первого члена ряда.
15.
При замене суммы S ряда, удовлетворяющего
признаку Лейбница, суммой его первых n
членов
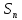 абсолютная величина совершённой ошибки
абсолютная величина совершённой ошибки![]() не
превышает абсолютной величины первого
из отброшенных
не
превышает абсолютной величины первого
из отброшенных![]()
Пример: Ряд
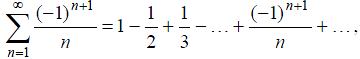
называемый рядом Лейбница, сходится по признаку Лейбница. В то же время, ряд, составленный из абсолютных величин его членов,
 расходится
(гармонический ряд).
расходится
(гармонический ряд).
Таким образом, ряд Лейбница - условно сходящийся ряд.
4. Степенные ряды
16. Ряд
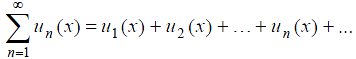
называется функциональным, если его члены являются функциями от x. Совокупность всех значений х, при которых этот ряд сходится, называется его областью сходимости. В области сходимости сумма функционального ряда S(x) есть функция от х.
17. Степенным рядом называется функциональный ряд вида
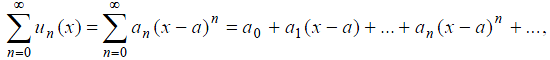 (1)
(1)
где (n = 0, 1, …) – числа, называемые коэффициентами ряда. При a = 0 ряд принимает вид
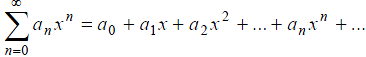 (2)
(2)
18. Область сходимости степенного ряда (2) есть симметричный относительно начала координат O интервал (–R, R), называемый интервалом сходимости ряда (2). Число R (0 ≤ R < +∞) называется радиусом сходимости ряда (2).
Радиус сходимости может быть вычислен по формулам
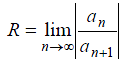 (3)
(3)
или
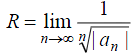 (4)
(4)
Степенной ряд (2) внутри интервала сходимости сходится абсолютно. Вне интервала сходимости ряд (2) расходится. При x = –R или x = R ряд (2) может оказаться расходящимся, сходящимся условно или сходящимся абсолютно.
19. Степенной ряд (1) сходится абсолютно на интервале (a–R; a+R).
20. Внутри интервала сходимости сумма степенного ряда есть непрерывная функция. Если пределы интегрирования лежат внутри интервала сходимости, то интеграл от суммы ряда равен сумме интегралов от членов ряда.
Пример 2: Найти область сходимости ряда. Исследовать сходимость ряда в концах интервала:
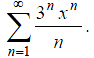
Решение:
Применим
формулу (3) для нахождения радиуса
сходимости. При этом
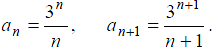
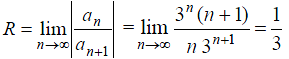
Таким
образом, ряд сходится абсолютно внутри
интервала
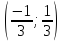 и
расходится вне этого интервала. Исследуем
точки x=
и
расходится вне этого интервала. Исследуем
точки x=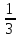 и
x=
и
x=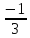 :
:
При
x=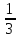 ряд
принимает вид
ряд
принимает вид
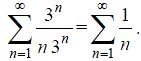
Это гармонический ряд, известно, что он расходится.
При
x=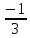 ряд
принимает вид
ряд
принимает вид
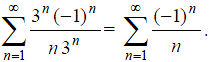
Это ряд Лейбница, он сходится условно (см. 15.).
Следовательно,
область сходимости данного ряда
 .
.
Ответ:
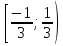 .
.
5. Ряд тейлора
21. Формула Тейлора.
Пусть функция )(xf имеет на некотором отрезке непрерывные производные до (n+1)-го порядка включительно, а точка a находится внутри этого отрезка. Тогда для любого x из этого отрезка имеет место формула Тейлора:
 ,
(1)
,
(1)
где остаточный член может быть записан в виде
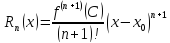 (2)
(2)
(форма
Лагранжа), причём c
лежит
между
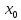 и
x.
и
x.
22.
Если функция
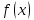 имеет
производные всех порядков на некотором
отрезке, содержащем внутри себя точку
x
=
имеет
производные всех порядков на некотором
отрезке, содержащем внутри себя точку
x
=
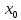 ,
и выполняется условие
,
и выполняется условие
![]() (3)
(3)
для всех x из указанного отрезка, то функция на этом отрезке является суммой степенного ряда:
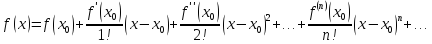 (4)
(4)
Этот ряд называется рядом Тейлора для данной функции. Говорят, что функция разложена в ряд Тейлора на этом отрезке.
В
случае
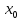 =
0 ряд Тейлора принимает вид
=
0 ряд Тейлора принимает вид
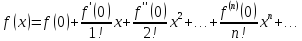 (5)
(5)
Этот ряд называется рядом Маклорена для данной функции.
23. При разложении функций в степенные ряды часто используются разложения в ряд Маклорена следующих функций:
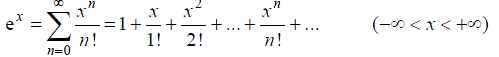 (6)
(6)
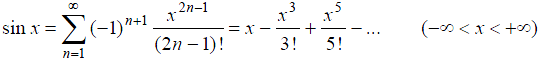 (7)
(7)
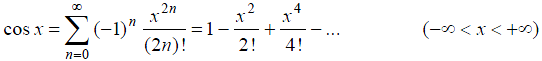 (8)
(8)
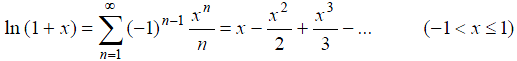 (9)
(9)
![]()
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
В скобках указаны промежутки, на которых верны указанные разложения.
