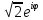- •Министерство образования, науки и молодежи республики крым гбпоу рк «керченский политехнический колледж»
- •Методические рекомендации
- •Методические рекомендации:
- •Тематический план
- •Раздел 2. Линейная алгебра
- •Раздел 3. Основы математического анализа
- •Раздел 4. Основы интегрального и дифференциального исчисления
- •Раздел 6. Дифференциальные уравнения
- •Раздел 8. Элементы теории вероятностей и математической статистики
- •Числовые характеристики выборки.
- •Раздел 3. Основы математического анализа
- •1.Числовые ряды
- •2. Ряды с положительными членами.
- •3. Знакопеременные ряды
- •4. Степенные ряды
- •5. Ряд тейлора
- •Задания контрольной работы Комплексные числа
- •Линейная алгебра.
- •Основы математического анализа Основы интегрального и дифференциального исчисления
- •Дифференциальные уравнения
- •Элементы теории вероятностей и математической статистики
- •Рекомендованная литература
- •Интернет-ресурсы:
Тематический план
Раздел 1. Комплексные числа
Тема 1.1. Комплексные числа
Раздел 2. Линейная алгебра
Тема 2.1. Матрицы и определители
Тема 2.2. Методы решения систем линейных уравнений
Раздел 3. Основы математического анализа
Тема 3.1. Предел функции
Тема 3.2. Ряды
Раздел 4. Основы интегрального и дифференциального исчисления
Тема 4.1. Дифференциальное исчисление
Тема 4.2. Интегральное исчисление.
Раздел 5. Дифференциальное исчисление многих переменных
Тема 5.1. Дифференциальное исчисление многих переменных
Раздел 6. Дифференциальные уравнения
Тема 6.1. Дифференциальные уравнения
Раздел 7. Основные понятия дискретной математики
Тема 7.1. Основные понятия дискретной математики
Раздел 8. Элементы теории вероятностей и математической статистики
Тема 8.1.Элементы теории вероятностей
Тема 8.2.Элементы математической статистики
Методические рекомендации по выполнению контрольной работы
Раздел 1. Комплексные числа
Комплексным
числом
z наз. выражение вида z
= x + iy,
где x
и
y
-
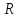 числа, а
числа, а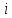 - мнимая единица,
- мнимая единица,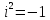 .
.
z = x + iy - алгебраическая запись к. ч.
Два
к. ч.
 и
и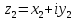 наз.равными,
если равны их действительные и мнимые
части, т. е.
наз.равными,
если равны их действительные и мнимые
части, т. е.
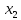 и
и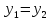 .
.
Числа 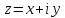 и
и 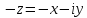 называются
противоположными
комплексными
числами.
называются
противоположными
комплексными
числами.
Два
к. ч.
 и
и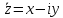 ,
которые отличаются лишь знаком мнимой
части, называютсясопряженными.
,
которые отличаются лишь знаком мнимой
части, называютсясопряженными.
Пример
1:
Решить квадратное уравнение 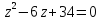
Решение:
Вычислим дискриминант:
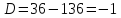 00
Дискриминант
отрицателен, и в действительных числах
уравнение решения не имеет. Но корень
можно извлечь в комплексных числах.
00
Дискриминант
отрицателен, и в действительных числах
уравнение решения не имеет. Но корень
можно извлечь в комплексных числах.
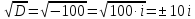
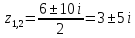
Ответ:
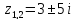
Действия над к.ч., записанными в алгебраической форме:
Сумма к. ч.: z1 + z2 = (x1 + x2) + i(y1 + y2);
Разность к. ч. : z1 - z2 = (x1 - x2) + i(y1 - y2);
Произведение к. ч. : z1 ∙z2 = (x1x2 - y1y2) + i(x1y2 + x2y1), (можно умножить многочлен на многочлен )
Деление двух к. ч.:
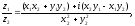 z2
z2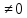
Действия над комплексными числами в тригонометрической форме:
Пусть z1 = r1(cos φ1 + isin φ1), z2 = r2(cos φ2 + isin φ2). Тогда:
Умножение
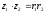 (cos(
(cos(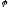 1+
1+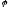 2)
+isin(
2)
+isin( 1+
1+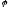 2))
2))
Вообще для любого z ≠ 0и для любогоn ϵ ℕ справедливо.
zn = rn(cos(nφ) + isin(nφ))– формула возведения в степень (I-я формула Муавра).
Операция извлечения корня n-ой степени из к. ч. определяется как обратная операци возведеня в степень:
К.
ч. zназ.корнем
n-ой степени
из числа (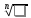 =z), еслиzn
= . Если
≠ 0, то
=z), еслиzn
= . Если
≠ 0, то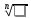 имеетnразличных
значений, определяемых по формуле
имеетnразличных
значений, определяемых по формуле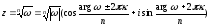 ,k=
,k=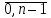 ,
-II-я формула Муавра
,
-II-я формула Муавра
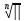 -
арифметическое значение корня из
положительного числа.
-
арифметическое значение корня из
положительного числа.
Деление (z2 ≠ 0):
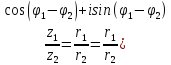
Пример
2:
Вычислить:
a)
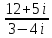 ;
;
Решение:
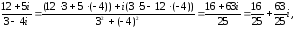
б)
Решение:
Представим комплексное число z
=-1+i
в тригонометрической форме

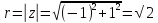
cos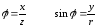
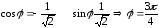
Значит
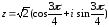
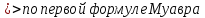
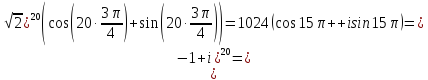 1024(-1
+
1024(-1
+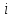 ∙ 0) = -1024
∙ 0) = -1024
Ответ:
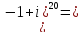 -1024
-1024
в)
Найти

Решение:
Представим комплексное число z
=-1+i
в тригонометрической форме

z
= -1 + i
=
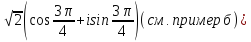 , тогда поII
формуле Муавра
, тогда поII
формуле Муавра
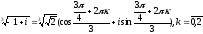
Тогда имеем три значения корня:
z1
=
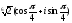 (k
=
0)
(k
=
0)
 (k
= 1)
(k
= 1)
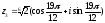 (k
= 2)
(k
= 2)
Ответ:
z1
=
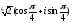 (k
=
0)
(k
=
0)
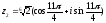 (k
= 1)
(k
= 1)
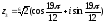 (k
= 2)
(k
= 2)
Пример
3:
Сложить два комплексных числа
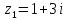 ,
,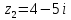
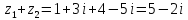
Найти
произведение комплексных чисел 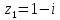 ,
,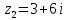
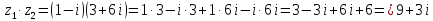
причем
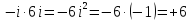
Найти частное:
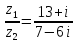
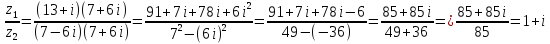
Показательная форма комплексного числа:
Символом eiφ обозначается
комплексное число cosφ+isinφ. С
помощью этого обозначения всякое
комплексное число z=r(cosφ+isinφ) может
быть представлено в показательной форме
![]()
Пример 4: Найти показательную форму числа z =-1+i
Решение:
Находим
модуль и аргумент числа:
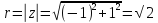
cos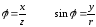
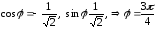
Следовательно,
показательная форма комплексного числа
такова:
z=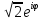
Ответ:
z=