
- •1.Матрица, операции над м. Опред-ли м.
- •2. Декартовая система координат на плоскости. Осн. Задачи.
- •3. Прямая. Угловой коэф. Прямой. Уравнение прямой с угл. Коэффициентом.
- •4. Общее ур-ние прямой, ур-ние прямой, проход. Ч/з 2 точки, ур-ние прямой в отрезках.
- •5. Угол между 2мя прямыми. Условия пар-сти и перп-сти 2х прямых.
- •6. Ур-ние плоскости в пространстве. Взаимное расположение плоскостей.
- •7. Векторы. Сложение, вычитание векторов, умножение вектора на число.
- •8. Операции над векторами, заданными в координатной форме.
- •9. Скалярное произведение векторов, его свойства.
- •10. Векторное произведение векторов, его свойства.
- •11. Системы линейных алгебраических уравнений. Решение их методами Гаусса, Крамера, матричным.
- •12. Линейная зависимость векторов. Разложение вектора по базису
- •13. Последовательности. Предел послед-сти.
- •14. Два замечательных предела
- •15. Функции. Непрерывность функции в точке и в области
- •16. Производная ф-ции. Смысл.
- •17. Произв. Сложной и обр. Ф-ции.
- •18. Дифф. Функции одной переменной, его геометр. Смысл. Применения дифф. В приближённых вычислениях.
- •19 Экстремум функции. Необходимое усл.
- •20. Исследование функции.
- •21. Первообр. Функции и неопр. Интеграл. Св-ва неопр. Инт. Таблица неопр. Интегр.
- •31. Линии уровня. Градиент.
- •22. Интегрирование по частям и замена переменных в неопределённом интеграле.
- •23. Опред. Интеграл. Осн. Свойства опред. Интеграла.
- •24 Теорема Ньютона-Лейбница.
- •25.Замена переменной и интегрирование по частям в определенном интеграле.
- •26.Площадь плоской фигуры. Объем тела вращения.
- •27. Несобственные инт. 1го и 2го порядка.
- •28. Среднее значение ф-и на отрезке. Теорема о среднем значении ф-и.
- •30. Экстремум ф-и нескольких переменных. Необходимое усл-е эктремума.
- •29. Ф-и нескольких переменных.
- •32. Частные производные ф-й 2-х переменных.
- •33. Полный дифференциал ф-й 2-х переменных.
- •34. Частные производные высших порядков.
- •35. Независимость частных производных от порядка дифференцирования.
- •36. Метод наименьших квадратов.
- •37. Числовые ряды, частные суммы числовых рядов.
- •38. Признаки сходимости ряда
- •39. Теоремы о сходимости числовых рядов.
- •40. Эталонные ряды для установления сходимости
- •41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена
- •42.Теорема Абеля о сходимости степенного ряда:
- •43. Разложение основных элементарных функций.
- •44. Показательная и тригонометрическая функция комплексной переменной, их связь
- •45. Ряд Фурье. Коэффициенты ряда Фурье. Сходимость рядов Фурье.
- •46. Дифференциальные уравнения (основные понятия)
- •47. Дифференциальные ур-я 1-го порядка с разделяющимися переменными:
- •49. Линейные дифференциальные уравнения с постоянными коэффициентами
- •50. Линейные однородные и линейные неоднородные дифференциальные уравнения 1-го порядка
21. Первообр. Функции и неопр. Интеграл. Св-ва неопр. Инт. Таблица неопр. Интегр.
Функция F(x) наз-ся первообразной ф-ции f(x) на определенном интервале, если
F'(x)=f(x) или dF(x)=f(x)dx.
Неопр. Интеграл- совок. всех первообр. для f(x), определенная на интерв. Х(∫f(x)dx=F(x)+c Осн. теор. интегрирования: Если ф-ция f(x), опред. на интер. x , имеет 1 первообразную F(x), то она имеет бесконечное число первообразных, все они описываются выр-ем F(x)+c, где c-const. Свойства:
постоянную можно вынос. за знак интег.
интеграл суммы равен сумме интегралов
произв. от инт. равна подынтегр. функции
интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.


31. Линии уровня. Градиент.
Линией уровня функции называется множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение.
ЛУ – такая линия в плоскости x и y, для кот. все значения z одинаковы. z=x2+y2 ; y=√z-x2 ; z=f(x,y).
Градиентом функции f(x)называется вектор, указывающий направление наиболее быстрого возрастания функции, и, стало быть, ориентированный перпендикулярно линиям уровня.
Для линейной
функции двух переменных линия уровня
представляет собой прямую, перпендикулярную
вектору с, который служит градиентом
данной функции. Следовательно, если
линия уровня определяется
уравнением f(x)=c1x1+ c2x2 =const, то этот
вектоp имеет вид
 и указывает направление возрастания
функции.
и указывает направление возрастания
функции.
22. Интегрирование по частям и замена переменных в неопределённом интеграле.
Интег. по частям
— один из способов нахожд. интеграла.
Суть метода:: если подынтегральная
функция может быть представлена в виде
произвед. двух непр. и гладких функций
(каждая из которых может быть как
элементарной функцией, так и композицией),
то справедлива следующая формула для
неопределённого интеграла:
![]()
Для упрощения
вычисления интеграла часто удобно
выполнить замену переменной. Переход
от x к новой переменной u описывается
выражением
![]()
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
дифф. dx должен быть заменен на дифф. новой переменной du. Для опред. инт., необход. также измен. пределы интегр-ния.

23. Опред. Интеграл. Осн. Свойства опред. Интеграла.
Определенный
интеграл - это функция, производная от
которой дает подынтегральную функцию.
ОИ ф-ции y=f(x)
на отрезке
 наз-ся предел инт-ых сумм.
наз-ся предел инт-ых сумм.
Свойства:
Свойства определённого интеграла:




 ,
то
,
то


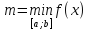 ,
,
 ,
то
,
то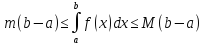
 ф-я
ф-я
 непрерывна на отрезке
непрерывна на отрезке ,
, ,то
на этом отрезке сущ. хотя бы одна точка
,то
на этом отрезке сущ. хотя бы одна точка ,
, такая,
что
такая,
что

 −я
−я
 непрерывна
и
непрерывна
и ,то
имеет место равенство
,то
имеет место равенство Ф-я
Ф-я наз.
определённым интегралом с переменным
верхним пределом.
наз.
определённым интегралом с переменным
верхним пределом.
24 Теорема Ньютона-Лейбница.
Теорема:
Опред. интеграл от непрерывной ф-ции
равен разности значений любой ее
первообразной для верхнего и нижнего
предела интегрирования. Формула
Ньютона-Лейбница связывает неопред и
опред интегралы. Если ф-ция y=f(x)
непрерывна на отрезке
 ,а
ф-цияF(x)-какая-либо
ее первообразная (т.е. F’(x)=f(x)),
то
,а
ф-цияF(x)-какая-либо
ее первообразная (т.е. F’(x)=f(x)),
то
 .
Эта формула сводит нахождение опред
интегр к нахождению неопред интегр.
РазностьF(b)-F(a)
обозначается F
.
Эта формула сводит нахождение опред
интегр к нахождению неопред интегр.
РазностьF(b)-F(a)
обозначается F .
.
Формула Ньютона – Лейбница.
Формула Ньютона – Лейбница связывает неопределенный и определенный интегралы.
Если
функция y=f(x)
непрерывна на отрезке [a,b]
,а функция F(x)—какая-л.
ее первообразная (т.е. F’(x)=f(x)),
то

