Властивості неперервних функцій.

1) Сума, різниця й добуток неперервних у точці х₀функцій – є функція, неперервна в точціх₀.

2) Частка двох неперервних функцій є неперервна функція за умови, щоg(x) не дорівнює нулю в точціх₀.

3) Суперпозиція неперервних функцій є неперервною функцією. Ця властивість може бути записана в такий спосіб:

Якщо u=f(x),v=g(x) – неперервні функції в точціх=х₀, то функціяv=g(f(x)) – теж неперервна функція в цій точці.

Справедливість наведених вище властивостей можна легко довести, використовуючи теореми про границі.

Неперервність деяких елементарних функцій.

1) Функція f(x) =C,C= const – неперервна функція на всій області визначення.

2) Раціональна функція неперервна для всіх значеньх, крім тих, при яких знаменник обертається в нуль. Таким чином, функція цього виду неперервна на всій області визначення.

3) Тригонометричні функції неперервні на своїй області визначення.

Доведемо властивість 3 для функції y= sinx.

Запишемо приріст функції , або після перетворення:

Дійсно, є границя добутку двох функцій і. При цьому функція косинус обмежена функція прих0, а оскільки границя функції синус, то вона є нескінченно малою прих0.

Таким чином, є добуток обмеженої функції на нескінченно малу, отже цей добуток, тобто функція у– нескінченно мала. Відповідно до розглянутого вище визначеннями, функціяу= sinx– неперервна функція для будь-якого значеннях=х₀з області визначення, тому що її приріст у цій точці – нескінченно мала величина.

Аналогічно можна довести неперервність інших тригонометричних функцій на всій області визначення.

Взагалі варто відмітити, що всі основні елементарні функції неперервні на всій своїй області визначення.

Точки розриву і їхня класифікація.

Розглянемо деяку функцію f(x), неперервну в околиці точких₀, за винятком може бути самої цієї точки. З визначення точки розриву функції треба, щобх=х₀була точкою розриву, якщо функція не визначена в цій точці, або не є в ній неперервною.

Слід зазначити також, що неперервність функції може бути однобічною. Пояснимо це в такий спосіб.

Якщо однобічна границя (див. вище) , то функція називається неперервною праворуч.

х₀

Якщо однобічна границя (див. вище) , то функція називається неперервною ліворуч.

х₀

Визначення.Точках₀називаєтьсяточкою розриву функціїf(x), якщоf(x) не визначена в точціх₀або не є неперервною в цій точці.

Визначення.Точках₀називаєтьсяточкою розриву 1-го роду, якщо в цій точці функціяf(x) має скінченні, але не рівні між собою ліву і праву границі.

Для виконання умов цього визначення непотрібно, щоб функція була визначена в точці х=х₀, достатньо того, щоб вона була визначена ліворуч і праворуч від неї.

З визначення можна зробити висновок, що в точці розриву 1-го роду функція може мати тільки скінченний стрибок. У деяких окремих випадках точку розриву 1-го роду ще іноді називають усувною точкою розриву, але докладніше про це поговоримо нижче.

Визначення.Точках₀називаєтьсяточкою розриву 2-го роду, якщо в цій точці функціяf(x) не має хоча б одної з однобічних границь або хоча б одна з них нескінченна.

Приклад.Функція Діріхле (Діріхле Петер Густав (1805–1859) – німецький математик, член-кореспондент Петербурзької АН з 1837р.)

не є неперервною в будь-якій точці х₀.

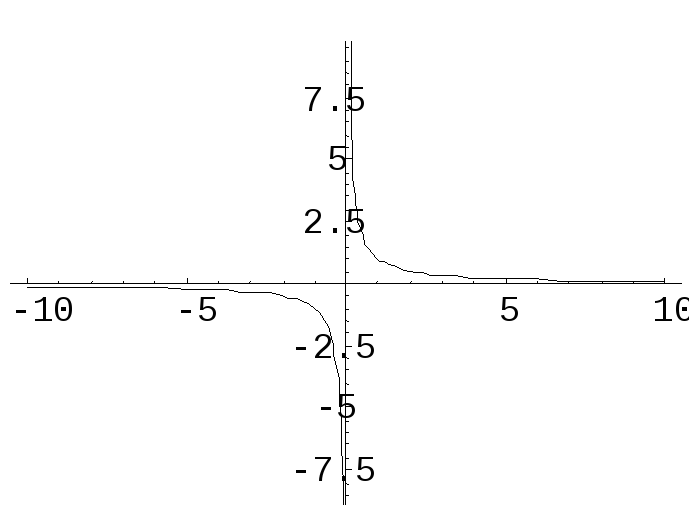
Приклад.Функціяf(x) =має в точціх₀= 0 точку розриву 2-го роду, тому що

.

Приклад.

Функція невизначена в точці х= 0, але має в ній кінцева границя, тобто в точціх= 0 функція має точку розриву 1-го роду. Це – усувна точка розриву, тому що якщо довизначити функцію:

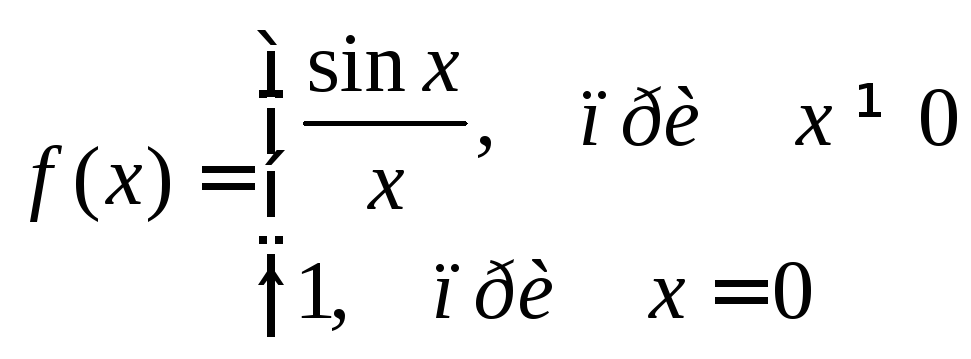
Графік цієї функції:

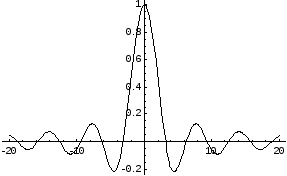
Приклад.

y

1

0 x

–1

Ця функція також позначається sign(x) – знакх. У точціх= 0 функція не визначена. Оскільки ліва й права границі функції різні, то точка розриву – 1-го роду. Якщо довизначити функцію в точціх= 0, поклавшиf(0) = 1, то функція буде неперервна праворуч, якщо покластиf(0) = –1, то функція буде неперервною ліворуч, якщо покластиf(x) рівне якому-небудь числу, відмінному від 1 або –1, то функція не буде неперервна ні ліворуч, ні праворуч, але у всіх випадках проте буде мати в точціх= 0 розрив 1-го роду. У цьому прикладі точка розриву 1-го роду не є усувною.

Таким чином, для того, щоб точка розриву 1-го роду була усувною, необхідно, щоб однобічні границі праворуч і ліворуч були скінченні й рівні, а функція була б у цій точці не визначена.