ЛЕКЦІЯ 7.

СИСТЕМИ ВИПАДКОВИХ ВЕЛИЧИН.

ГРАНИЧНІ ТЕОРЕМИ ТЕОРІЇ ЙМОВІРНОСТЕЙ

1. Поняття та закон розподілу системи випадкових величин

2. Система двох випадкових величин

3. Числові характеристики системи двох випадкових величин. Кореляційний момент, коефіцієнт кореляції і рівняння регресії

4. Багатовимірний розподіл. Числові характеристики системи довільного числа випадкових величин

5. Функції випадкових величин. Числові характеристики. Кореляційна матриця системи функцій випадкових

6. величин

7. Граничні теореми теорії ймовірностей

1. Поняття та закон розподілу системи випадкових величин

До цього часу ми розглядали одномірну випадкову величину Х. Однак в сучасній теорії математичної обробки результатів багаторазових повторних геодезичних вимірювань використовують багатомірні випадкові величини. Багатомірна випадкова величина може складатися із декількох компонентів і бути двомірною, тримірною і так далі. Так, наприклад, координати точки на площині визначаються двома випадковими величинами: абсцисою Х та ординатою Y; положення точки в просторі визначається вже трьома координатами - Х, Y та висотою Н.

Сумісна дія двох чи більше випадкових величин приводить до системи випадкових величин. Умовимось систему декількох випадкових величин Х, Y, ..., N позначати (Х, Y, …, N). При вивченні системи випадкових величин визначають характеристики як кожної випадкової величини, так і зв’язки та залежність між ними. А це вже більш складні задачі.

Домовимось, що систему двох випадкових величин (Х,Y) ми будемо розглядати як випадкову точку на площині х0у з координатами Х і Y, або як випадковий вектор на площині з випадковими складовими X і Y. Систему трьох випадкових величин (X, Y, Z)  як випадкову точку в тримірному просторі або, як випадковий вектор в просторі. За аналогією, систему п-випадкових величин (Х, Y, …, N) розглядають як випадкову точку в п-мірному просторі або, як п-мірний випадковий вектор.

Законом розподілу системи випадкових величин називають співвідношення, що встановлює зв’язок між областями можливих значень системи випадкових величин і ймовірностями появи їх в цих областях.

Закон розподілу системи випадкових величин можна задавати в різних формах. Покажемо табличний спосіб розподілу системи дискретних випадкових величин.

Якщо Х та Y  дискретні випадкові величини, значення яких дорівнюють (Х_і,Y_j), де і = , а j = , то їх розподіл системи можна характеризувати ймовірностями p_ij = P(X = x_і; Y = y_j). Це означає, що коли випадкова величина Х приймає значення х_і, одночасно і величина Y прийме значення у_j.

Ймовірність р_ij зводять до табл. 3.1. Її називають таблицею розподілу системи двох дискретних випадкових величин

Таблиця 3.1

Хі Yі	х1	х2	...	хп
y1	p11	p21	…	pn1
y2	p12	P22		Pn2
…	…	…	…	…
ym	p1m	p2m		Pnm

Всі можливі події (X = x_i; Y = y_j) при і = і j = складають повну групу несумісних подій і тому

(X = x_i, Y = y_j) = 1. (1)

2. Система двох випадкових величин

В практиці геодезичних вимірів досить часто взаємодіють дві випадкові величини Х та Y, тобто двомірні випадкові величини. Так, наприклад, координати точки на площині визначаються двома випадковими величинами: абсцисою Х та ординатою Y; положення точки в просторі визначається вже трьома координатами - Х, Y та висотою Н.

При лінійних вимірах взаємодіють - довжина мірного приладу та температура. При дослідженнях деформацій інженерних споруд взаємодіють - величина осідання та інтервал часу і так далі.

Закон розподілу системи двох випадкових величин задають функцією розподілу та щільністю розподілу.

Функцією розподілу системи двох випадкових величин називають функцію двох аргументів F(x,y), що дорівнює ймовірності сумісного виконання двох нерівностей X < x i Y < y, тобто

F(x,y) = P(X < x i Y < y). (2)

Геометрично функцією розподілу системи двох випадкових величин є ймовірність попадання випадкової точки (Х,Y) в нескінченний квадрат площини (рис. 1) з вершиною в точці (х,у).

Функція розподілу має такі властивості:

1. Якщо один із аргументів наближається до плюс нескінченності, то функція розподілу системи наближається до функції розподілу випадкової величини другого аргументу, тобто

F (x, +) = F₁(x);

F (+, y) = F₂(y).

2. При наближенні обох аргументів до плюс нескінченності функція розподілу F (x,y) наближається до одиниці:

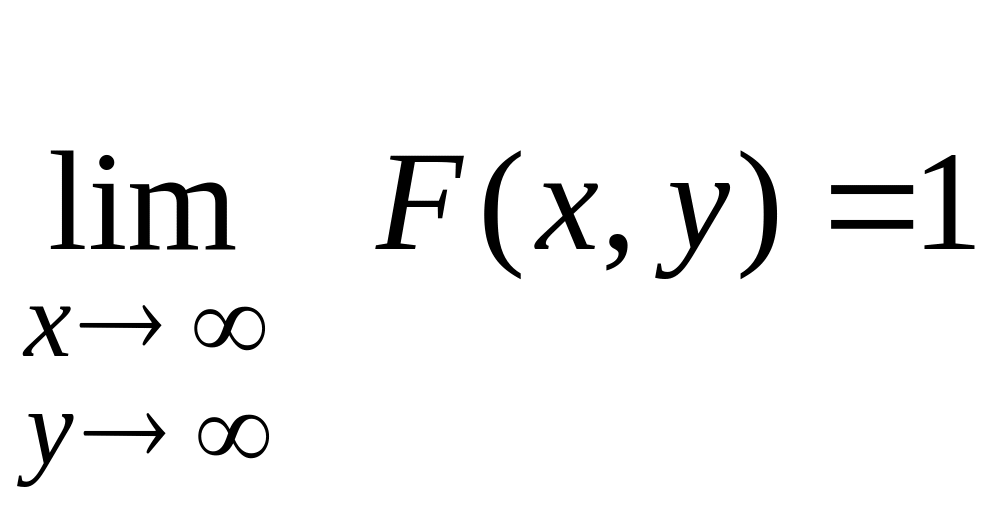, або F (+, +) = 1.

3. При наближенні одного чи обох аргументів до мінус нескінченності функція розподілу наближається до нуля:

,

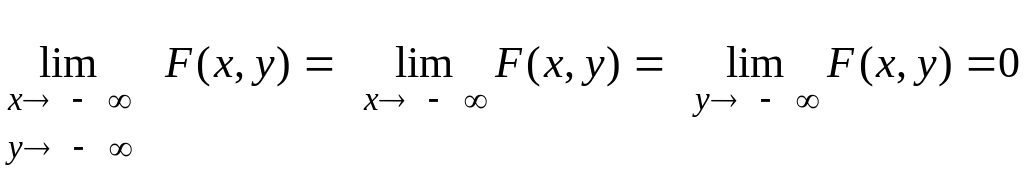або F (- , у) = F ( х, - ) = F (- , - ) = 0.

4. Функція розподілу (F (х, у) є зростаючою функцією з кожного аргументу:

F ( x₂, y)  F (x₁, y), якщо х₂ > x₁;

F ( x, y₂)  F (x, y₁), якщо у₂ > у₁.

5. Ймовірність попадання випадкової точки (х,у) в будь-який прямокутник зі сторонами, паралельними координатним осям, обчислюється за формулою

F ( x₂, y₂)  F ( x₁, y₂) 

 F ( x₂, y₁) + F ( x₁, y₁). (3)

Це легко з’ясувати геометрично, якщо уявити положення прямокутника з координатами вершин А( x₁, y₁), В( x₁, y₂) , С( x₂, y₂) і D( x₂, y₁) на рис. 1 і геометричними значеннями функцій F( x₂, y₂), …, F( x₁, y₁) в формулі (3).

Практичне значення мають системи неперервних випадкових величин, розподіл яких характеризують щільністю розподілу (x, y). За допомогою неї більш просто знаходять імовірність попадання в різні області, а опис розподілу системи випадкових величин стає більш наочним.

Щільність розподілу системи двох випадкових неперервних величин визначають як другу змішану часткову похідну від функції F(x,y), тобто

(х,у) = 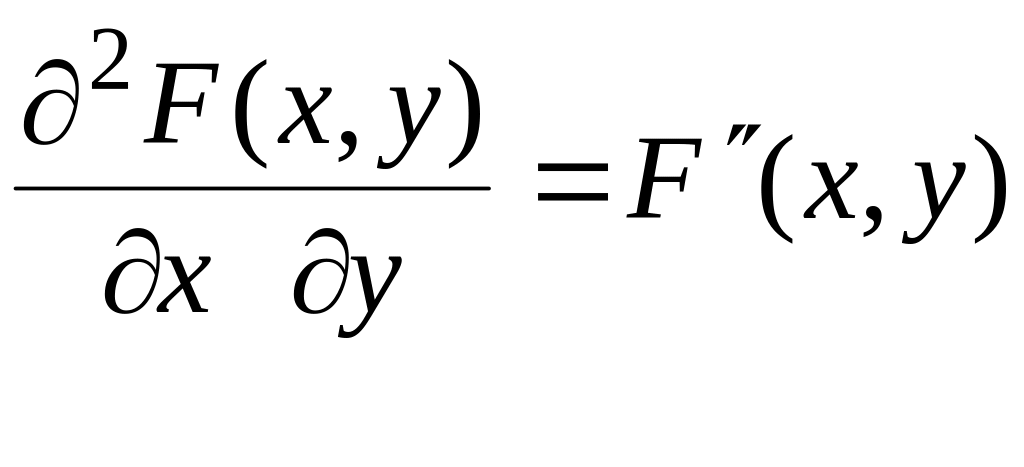. (4)

Геометрично функцію (х,у) можна виразити просторовою поверхнею, що нагадує перевернутий до низу дзвоник, краї якого віддаляються до нескінченності, асимптотично наближаючись до площини х0у (рис. 2). Її називають поверхнею розподілу.

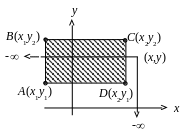
Рис. 1

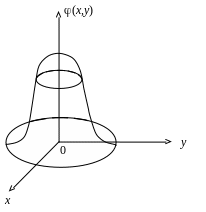
Рис. 2

Функція розподілу F(x,y) визначається за формулою

F(x,y) = (x,y) dxdy. (5)

Щільність розподілу системи двох випадкових величин має властивості:

1. Щільністю розподілу є функція

(x,y)  0.

2. Подвійний інтеграл з нескінченними межами від функції щільності розподілу дорівнює одиниці:

(x,y) dxdy = 1.

Геометрично це свідчить про те, що об’єм тіла, відмежованого поверхнею розподілу і площиною х0у, дорівнює одиниці.

Щільності розподілу величин х та у, що входять в систему, визначають за формулами:

₁(х) = (x,y) dy ;

₂ (у) = (x,y) dх .

Тобто, для визначення щільності розподілу однієї із системи випадкових величин, треба проінтегрувати в необмежених межах щільність розподілу системи (х,у) за аргументом другої випадкової величини.

Якщо відомі щільності розподілу окремих випадкових величин системи і випадкові величини х та у незалежні між собою, то можна визначити закон їх сумісного розподілу за формулою

(х,у) = ₁(х)  ₂ (у).

Подібно умовній імовірності Р для подій визначають умовні щільності розподілу:

1)   щільність розподілу y при умові, що випадкова величина Х прийняла значення х;

2)   щільність розподілу х при умові, що випадкова величина Y прийняла значення у.