
QuantMech_Chem_p3_85
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Обнинский государственный технический университет атомной энергетики (ИАТЭ)
Факультет естественных наук
Ф.И. Карманов, А.Н. Евдокимов
Квантовая механика и квантовая химия
Компьютерный практикум по курсу «Квантовая механика и квантовая химия»
ОБНИНСК 2007
УДК
Карманов Ф.И., Евдокимов А.Н. Компьютерный практикум по курсу " Квантовая механика и квантовая химия". -- Обнинск, ИАТЭ, 2007. - 84 с.
Предназначено для студентов 4-го курса специальностей 510500 «Химия».
Пособие содержит описания и методические рекомендации к выполнению компьютерных работ по курсу «Квантовая механика и квантовая химия». В пособии рассматриваются постановки задач, формулируются методы их решения, обсуждаются алгоритмы и приводятся подробные тексты программ моделирования с использованием достаточно широких возможностей интегрированного пакета «MathCAD 11a». Пособие содержит материал, связанный с квантовомеханическим описанием осциллятора, атома водорода, применением вариационных методов и теории возмущений в квантовой механике, сложения моментов, элементов теории групп и представлений групп симметрии молекул, метода молекулярных орбиталей Хюккеля и др. Все результаты расчетов, иллюстрирующие текст, получены с помощью приведенных программ, которые могут быть использованы для интерактивного и вариантного анализа задач.
Рецензенты: к.ф.-м.н. В.А. Шакиров. д.ф.-м.н. В.К. Милинчук.
Темплан 2007, поз. ?.
Обнинский государственный технический университет атомной энергетики, 2007 г.
Ф.И. Карманов, А.Н. Евдокимов, 2007 г.
Наблюдаемые и их характеристики Задача 1
Пусть частица массой m движется в потенциальной яме с бесконечно высокими стенками. Используя решение задачи о собственных значениях для гамильтониана системы найти: а) зависимость плотности вероятности обнаружения частицы от ее координаты в яме; б) средние значения координаты, импульса и энергии частицы; в) проверить соотношение неопределенностей Гейзенберга для координат и импульсов частицы; г) коэффициенты разложения функции вида Ψ(x) = Ax (a2 - x2) по базису из собственных функций гамильтониана.
Решение
Волновые функции и плотность вероятности
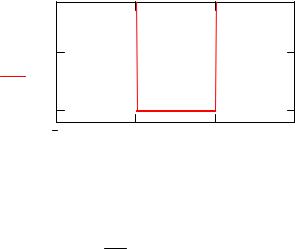
Пусть распределение потенциала задано в следующей форме.
d := 1 A |
Uo := 10 eV |
U(x) := if (0 < x < d ,0 ,Uo) |
U(x) 5
0
1 |
0 |
1 |
2 |
x
Рис. 1. Распределение потенциала
Тогда задача на собственные значения для области 0 < x < a с учетом граничных условий и условия нормировки будет иметь вид:
−h2 d2 Ψ(x) + U(x) Ψ(x) = E Ψ(x) 2 m dx2
⌠a
Ψ(0) = Ψ(a) = 0 Ψ(x) Ψ(x) dx = 1
⌡0
Решение этой задачи - волновые функции и спектр энергий (см. [1-3])
3

|
|
2 |
n π x |
E(n) = |
h2 π2 n2 |
|||
φ(n ,a,x) := |
a sin |
a |
|
2 m a |
2 |
|||
|
|
|
Ψ(n ,x) := if (0 < x < d ,φ(n ,d ,x) ,0) |
|
||||
|
2 |
|
|
|
|
|
|
|
Ψ(1,x) |
|
|
|
|
|
|
|
|
Ψ(2,x) |
0 |
|
|
|
|
|
|
|
Ψ(3,x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
0.5 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
|
|
|
Рис. 2. |
Волновые функции для трех первых состояний |
|||||||
Плотность вероятности обнаружить частицу в единичном интервале в |
||||||||
пределах ямы равна |
|
|
|
|
|
|
||
|
|
|
|
|
ρ(n ,x) := ( Ψ(n ,x) |
)2 |
|
|
ρ(1,x) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ(2,x) |
|
|
|
|
|
|
|
|
ρ(3,x) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0.5 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
|
|
|
|
Рис. 3. Плотность вероятности для первых состояний |
|||||||
Используя панель Symbolic и определяя значения sin(nπ) =0 для целых n, проверим условие нормировки волновой функции, а также вычислим вероятность обнаружить частицу в средней трети потенциальной ямы, например, в основном состоянии n = 1.
4

|
|
|
|
⌠a |
|
2 |
|
( |
) |
|
|
|
|
|
|
||
|
|
|
|
|
φ(n ,a,x) |
dx |
= 0 |
|
→ 1 |
|
|||||||
|
|
|
|
⌡ |
|
substitute,sin n π |
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
⌠ |
2 |
a |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
3 (φ(n ,a,x))2 dx |
|
|
|
|
|
|
3 3 2 |
|
|||||||||
|
|
|
|
substitute,n = 1→ |
1 |
|
+ 2 π |
||||||||||
|
|
|
|||||||||||||||
|
|
|
6 |
|
|
π |
|||||||||||
|
|
|
|
|
|
|
|
|
simplify |
|
|
|
|
|
|||
⌡a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Средние значения координаты, импульса и энергии
По определению, среднее значение координаты x состоянии, определяемом волновой функцией φ(n ,a,x), равно
|
⌠a |
|
|
|
|
|
( |
|
|
)2 |
= 1 |
|
|
|
x φ(n ,a,x)2 dx |
substitute,cos n π |
|
1 |
|
||||||||
Xav(n ,a) := |
|
simplify |
|
|
|
|
→ |
a |
|||||
|
⌡ |
|
|
|
substitute,sin(n π) = 0 |
2 |
|
||||||
|
0 |
|
|
|
|
|
|||||||
Среднее значение импульса для всех состояний равно нулю. |
|
i := −1 |
|||||||||||
|
|
|
⌠a |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Pav(n ,a,h) := |
φ(n ,a,x) |
−i h |
|
|
φ(n ,a,x) dx |
|
|||||||
dx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
⌡0 |
|
|
|
|
|
|
|
|
|
|
substitute,sin(n π) = 0 Pav(n ,a,h) cos(n π)2 = 1 → 0
Среднее значение потенциальной энергии, очевидно, равно нулю, а для кинетической - равно средней полной энергии в состоянии с номером n.
⌠a |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||
|
−h |
|
|
|
|
|
|
|
||||||
Eav(n ,a,h) := |
|
|
|
d |
|
φ(n ,a,x) |
|
|
|
|||||
φ(n ,a,x) |
|
|
|
|
dx |
|||||||||
2 m |
2 |
|||||||||||||
|
|
|
dx |
|
|
|
|
|
|
|||||
⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eav(n ,a,h) substitute,sin(n π) = 0 |
→ |
|
1 |
n2 π2 |
|
h2 |
|
|||||||
2 |
m |
|||||||||||||
|
|
|
|
|
|
|
a2 |
|
|
|||||
5
Соотношение неопределенностей Гейзенберга
По определению, дисперсия значений координат задается соотношением
|
|
|
⌠a |
|
a 2 |
|
|
|||
|
|
|
|
|
2 |
|
||||
|
Dx(n ,a) := |
|
|
|
|
|
|
|
||
|
x − |
2 φ(n ,a,x) dx |
||||||||
|
|
|||||||||
|
|
|
⌡0 |
|
|
|
|
|
|
|
и равна |
|
substitute,sin(n π) = 0 |
|
n2 π2 − 6 |
||||||
|
|
|||||||||
Dx(n ,a) |
( |
|
)2 |
= 1 |
|
→ |
1 |
a2 |
||
|
|
|
|
|||||||
|
|
cos n π |
|
12 |
|
n2 π2 |
||||
|
|
simplify |
|
|
||||||
|
|
|
|
|
|
|
|
|||
Поскольку среднее значение импульса равно нулю, то дисперсия значений импульса совпадает со средним квадратом импульса.
⌠a |
|
|
2 |
|
|
|
|
|
d |
|
|
||
P2av(n ,a,h) := −h2 |
φ(n ,a,x) |
|
|
φ(n ,a,x) |
||
dx2 |
||||||
|
|
|
||||
⌡0 |
|
|
|
|
|
|
Dp(n ,a,h) := P2av(n ,a,h) − Pav(n ,a,h)2
substitute,sin(n π) = 0
Dp(n ,a,h)
substitute,cos(n π)2 = 1
dx
a2
Произведение дисперсий по порядку величины равно h2.
|
substitute,sin(n π) = 0 |
1 |
(n2 π2 − 6)h2 |
||||
|
|||||||
Dx(n ,a) Dp(n ,a,h) |
( |
)2 |
= 1 |
→ |
|||
12 |
|||||||
|
cos n π |
|
|
|
|||
|
simplify |
|
|
|
|
||
Среднеквадратичные отклонения координат и импульсов задаются соотношениями
(n ,a) := Dx(n ,a) , p(n ,a,h) := Dp(n ,a,h) ,
а их произведение с точностью до 3-х значащих цифр, например, при n = 1 равно:
h |
n2 π2 |
− |
1 |
|
substitute,n = 1→ .567 h |
|
|
||||||
12 |
2 |
|||||
|
|
|
float,3 |
6

Разложение волновой функции по базису
Пусть волновая функция некоторого состояния имеет вид:
ψ(a,x) = A(a) x (a2 − x2)
Выполним нормировку и определим константу А(a)
⌠a |
x (a2 − x2) 2 dx → |
|
|
|
|
|
8 |
a7 |
A(a) := |
105 |
|
|
2 a3 2 a |
||||
⌡0 |
|
105 |
|
|
Проверим условие нормировки:
⌠a
A(a) x (a2 − x2) 2 dx → 1
⌡0
Найдем коэффициенты разложения функции ψ(a,x) по базису из соб-
ственных функций гамильтониана φ(n ,a,x). |
|
|
|
|
||||||
|
C(n ,a) := |
⌠a |
φ(n ,a,x) x (a2 − x2)dx |
|
|
|
||||
|
A(a) |
|
|
|
|
|||||
|
|
⌡0 |
|
|
|
|
|
|
|
|
|
assume,a > 0 |
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
1+n 105 2 |
||||||
|
|
( |
) |
= 0 |
|
|||||
C(n ,a) |
substitute,sin n π |
|
→ 3 (−1) |
|
|
|
|
|||
substitute,cos(n π) = (−1)n |
n3 π3 |
|||||||||
|
|
|
||||||||
simplify
Квадраты модулей коэффициентов разложения определяют вероятности обнаружить систему в состоянии с волновой функцией φ(n ,a,x).
|
P(n ,a) := C(n ,a)2 |
|
|
|
substitute,sin(n π) = 0 |
945 |
|
|
|||
P(n ,a) |
substitute,cos(n π)2 = 1→ |
||
n6 π6 |
|||
|
Как легко видеть, эти вероятности быстро убывают с ростом номера состояния и основной вклад вносит состояние с n =1.
P(1 ,a) float,6 → .982951
7
Выполним численные расчеты коэффициентов разложения. Сформируем приближенную волновую функцию Φ(m,x) и оценим изменения в этой волновой функции по мере увеличения количества учитываемых
в разложении базисных функций. |
Убедимся в ортонормированности |
|||||||||||||
базиса, вычислив интегралы перекрывания базисных функций. |
Пусть |
|||||||||||||
a := 1 |
n := 1 .. 5 |
m := 1 .. 5 |
ORIGIN := 1 |
ψ(x) := A(a) x (a2 − x2) |
||||||||||
C(n ,a)2 = |
|
|
S |
:= |
⌠a |
|
|
|
|
|
|
|||
|
|
|
φ(n ,a,x) φ(m,a,x) dx |
|
|
|
||||||||
|
|
|
|
|
n,m |
|
⌡ |
|
|
|
|
|
|
|
|
|
0.983 |
|
|
|
0 |
|
1 |
0 |
0 |
0 |
0 |
||
|
|
0.015 |
|
5 |
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
0 |
|
1.348·10 |
-3 |
|
∑ C(n |
,a) |
= 1 |
|
1 |
0 |
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2.4·10 |
-4 |
|
n = 1 |
|
|
|
|
S = 0 |
0 |
1 |
0 |
0 |
|
6.291·10 |
-5 |
|
|
|
|
|
|
0 |
0 |
1 |
|
|||
|
Средние значения энергии |
|
||||||||||||
|
|
|
|
|
|
0 |
0 |
|||||||
|
|
⌠a |
|
|
|
|
h := 1 mo := |
1 |
0 0 0 0 1 |
|||||
|
2 |
|
2 |
|
|
5 |
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
−h |
ψ(x) d |
|
2ψ(x) dx = 5.25 |
∑ C(n ,a)2 (n π h) |
|
= 5.24 |
||||||||
2 mo |
|
dx |
|
|
|
n = 1 |
|
2 mo a2 |
|
|||||
|
|
⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
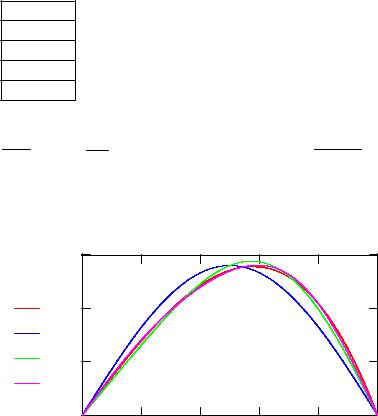
Φ(m,x) := |
∑ C(n ,a) φ(n ,a,x) |
|
|
|
|
||||
|
|
|
|
|
|
|
n = 1 |
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
ψ(x) |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
Φ(1,x) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Φ(2,x) |
|
|
|
|
|
|
|
|
|
|
|
|
||
Φ(3,x) |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
||
0 0 |
0.2 |
0.4 |
0.6 |
0.8 |
x
Рис. 5. Исходная и приближенная волновые функции. Как видно из рисунка, учет уже трех слагаемых позволяет с хорошей точностью воспроизвести исходную функцию
8
Упражнения
1.Вычислить средние значения координат, импульсов и энергии частицы в состоянии с волновой функцией вида ψ(x) = A x (a - x). Проверить соотношение неопределенностей Гейзенберга для координат и импульсов частицы.
2.В потенциальной яме с бесконечно высокими стенками в состоянии с волновой функцией ψ(x) находится частица. Определить вероятность ее пребывания в n-м квантовом состоянии и среднюю энергию, если
а) |
ψ(x) = A x (a - x); б) ψ(x) = A sin2 (πx/a). |
3. |
Для частицы в яме с бесконечно высокими стенками вычислить |
средние значения физических величин, отвечающих следующим комбинациям операторов координаты и импульса: xp, px, x2p и p2x .
4. Волновая функция одномерной системы имеет вид ψ(x) = Aexp(-x2/2a2). Здесь А - нормировочная константа, а - параметр. Найти вероятность обнаружить частицу в интервале -a < x < a. Вычислить средние значения координат, импульсов и их квадратов. Найти произведение x p.
5.Решить задачу о собственных значениях для оператора квадрата импульса в случае одномерного свободного движения частицы. Выполнить нормировку собственных функций с использованием дельта-функ- ции Дирака и найти средние значения координаты и импульса.
6.Волновая функция состояния частицы имеет вид
ψ(x) = A exp |
|
i p |
x |
Φ(x) |
, |
||
|
|
|
|||||
|
h |
||||||
|
o |
|
|
||||
где Φ(x) - вещественная функция. Показать, что p0 - средний импульс частицы в рассматриваемом состоянии.
7. В состоянии с трехмерной волновой функцией вида |
(0 < r < |
∞) |
|||||
|
(2n)! |
− 0.5 |
n−1 |
|
|
|
|
ψ(x) = |
|
|
|
r |
exp(−Zr) |
|
|
|
2n+1 |
|
|
||||
|
(2 Z) |
|
|
|
|
|
|
|
|
r , r2 , |
r− 2 , |
r− 1 . |
|||
вычислить средние значения величин |
|||||||
8. Определить возможные собственные значения оператора Lz и их вероятности для системы, находящейся в состоянии:
а) ψ(φ) = A sin2(φ); б) ψ(φ) = A(1+cos(φ))2 .
9
Коммутаторы эрмитовых операторов Задача 2
Используя возможности символьного процессора вычислить следующие коммутаторы: а) [X,Px] ; б) [H,X] ; в) [Lx,Ly] .
Решение
Коммутатор операторов координаты и импульса
Определим законы действия операторов координаты и проекции импульса на волновую функцию ψ. Пусть
X(x ,ψ) := x ψ |
i := −1 |
Px(h ,x ,ψ) := −i h |
d |
ψ |
|
||||
|
|
|
dx |
|
Проверим действие этих операторов на функцию ψ, зависящую от x.
X(x ,ψ(x)) → x ψ(x) |
Px(h ,x ,ψ(x)) → −i h |
d |
ψ(x) |
|
|||
|
|
dx |
|
Коммутатор операторов координаты и проекции импульса равен ([1-3]), где I - единичный оператор:
[X,Px] = ih I
Используя возможности символьного процессора MathCAD при подстановке и расширении аргументов функции, сформируем комбинацию, соответствующую произведению операторов в прямом порядке и обратном порядке и вычислим их:
X(x ,Px(h ,x ,ψ(x))) → −i x h |
d |
|
ψ(x) |
|||||
dx |
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
d |
|
||
Px(h ,x ,X(x ,ψ(x))) → −i h |
ψ(x) + x |
|
|
ψ(x) |
||||
dx |
||||||||
|
|
|
|
|
|
|||
А теперь собираем коммутатор и упрощаем полученное выражение с использованием команды simplify панели Symbolic:
X(x ,Px(h ,x ,ψ(x))) − Px(h ,x ,X(x ,ψ(x))) simplify → i h ψ(x)
Следовательно, |
[X,Px] ψ = ih ψ |
|
10
