
QuantMech_Chem_p3_85
.pdf
Коммутатор оператора координаты и гамильтониана
В качестве другого примера вычислим коммутатор гамильтониана и оператора координаты. Пусть U(x) - потенциальная энергия частицы массой m. Определим результат действия гамильтониана на волновую функцию следующим образом:
H(h ,m,U,x ,ψ) := −h2 d2 ψ + U ψ
2 m dx2
Собираем коммутатор и упрощаем полученное выражение. ComHX(h ,m,U,x ,ψ) := H(h ,m,U,x ,X(x ,ψ)) − X(x ,H(h ,m,U,x ,ψ))
d ψ(x) ComHX(h ,m,U(x) ,x ,ψ(x)) simplify → −h2 dx m
Принимая во внимание явный вид оператора проекции импульса, находим ответ.
[H,X] = −i mh Px
Коммутаторы операторов момента импульса
Определим явный вид операторов проекций момента импульса с помощью соотношений:
Lx(h ,x ,y ,z,ψ) := −i y h d ψ + i z h d ψ dz dy
Ly(h ,x ,y ,z,ψ) := −i z h d ψ + i x h d ψ dx dz
Lz(h ,x ,y ,z,ψ) := −i x h d ψ + i y h d ψ dy dx
Тогда операторы квадратов проекций момента импульса и его модуля можно задать следующим образом:
L2x(h ,x ,y ,z,ψ) := Lx(h ,x ,y ,z,Lx(h ,x ,y ,z,ψ))
L2y(h ,x ,y ,z,ψ) := Ly(h ,x ,y ,z,Ly(h ,x ,y ,z,ψ))
L2z(h ,x ,y ,z,ψ) := Lz(h ,x ,y ,z,Lz(h ,x ,y ,z,ψ))
L2(h ,x ,y ,z,ψ) := L2x(h ,x ,y ,z,ψ) + L2y(h ,x ,y ,z,ψ) + L2z(h ,x ,y ,z,ψ)
11

Вычислим следующий коммутатор проекций момента импульса.
[Lx,Ly] = ih Lz
Сначала вычислим произведение операторов в левой части равенства, а затем и сам коммутатор.
C1(h ,x ,y ,z,ψ) := Lx(h ,x ,y ,z,Ly(h ,x ,y ,z,ψ))
C2(h ,x ,y ,z,ψ) := Ly(h ,x ,y ,z,Lx(h ,x ,y ,z,ψ))
Com(h ,x ,y ,z,ψ) := C1(h ,x ,y ,z,ψ) − C2(h ,x ,y ,z,ψ)
Com(h ,x ,y ,z,ψ(x ,y ,z)) simplify → −y h2 d ψ(x ,y ,z) + x h2 d ψ(x ,y ,z)
dx |
dy |
Для проверки правильности результата сопоставим его с произведением ih Lz и находим
i h Lz(h ,x ,y ,z,ψ(x ,y ,z)) simplify → h |
2 |
|
d |
|
d |
|
||
|
x |
|
|
ψ(x ,y ,z) − y |
|
|
ψ(x ,y ,z) |
|
|
dy |
dx |
||||||
|
|
|
|
|
||||
Упражнения
1. Проверить следующие равенства для коммутаторов:
а) [X,Py] = 0 , б) [Px,Py] = 0 , в) [f(x),Px] =i h d f(x) dx
2. Вычислить коммутаторы: а) [X,Px2] ; б) [X2,Px]; в) [X2,[X,Px2]] .
3. |
Проверить равенство: |
а) [H,Px] =i h |
d |
|
U(x) |
|||||
|
|
|||||||||
|
|
|
|
|
|
dx |
|
|||
|
б) [H,Px2] = 2 i h |
d |
|
U(x) Px + h2 |
d2 |
|
U(x) |
|
||
|
dx |
dx2 |
|
|||||||
|
|
|
|
|
|
|||||
4. |
Проверить следующие правила коммутации: |
|
||||||||
|
а) [X,Lx] = 0 , |
б) [Y,Lx] = - ih Z , |
|
|
в) [Z,Lx] = ihY . |
|||||
|
г) [Px,Lx] = 0 , |
д) [Lx,Py] = ih Pz , |
|
|
е) [Lx,P2] = 0 . |
|||||
5. |
Проверить следующие правила коммутации: |
|
||||||||
|
а) [T,L2] = 0 , |
|
|
б) [Lx,Ly] = ih Lz , |
в) [L2,Lz] = 0 . |
|||||
6. |
Доказать, что [L+,L--] = 2h Lz , где L+ = Lx + i Ly и L-- = Lx - i Ly . |
|||||||||
12
Квантовый гармонический осциллятор Задача 3
Для частицы массой m движущейся в потенциальном поле квазиупругой силы найти: а) зависимость плотности вероятности обнаружения частицы от ее координаты и сопоставить с решением задачи о классической частице; б) дисперсии значений координат, импульсов и вычислить произведение неопределенностей основном состоянии осциллятора; в) проверить, что матричные элементы оператора координаты в базисе из собственных функций гамильтониана определяются соотношениями:
<n -1| X |n> = b (n/2)1/2 , <n +1| X |n> = b ((n+1)/2)1/2 .
Решение
Классический осциллятор
Пусть параметры потенциала соответствуют частоте колебаний молекулы водорода, а масса частицы - приведенная масса двух атомов водорода.
ω := 7.82 1014 rad s− 1 m := 0.5 1.672 10− 24 g
Оценим константу упругости связи (силовую постоянную), равную
|
|
2 |
|
|
2 |
|
|
|
5 |
|
|
− 2 |
dyn |
|
− 2 |
|
k = m ω |
|
m ω |
|
= 5.112 |
× 10 |
|
g s |
= cm |
= erg cm |
|
||||||
|
или |
|
|
5.112 × 105 |
|
= 31.95 |
eV |
|
|
|||||||
|
|
1.6 10− 12 1016 |
A2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Оценим энергию кванта |
hω := 0.659 10− 15 ω |
hω = 0.515 eV |
||||||||||||||
Пусть |
k := 32.0 eV A− 2 |
E = |
|
p2 |
|
+ k |
x2 |
U(x) := 0.5 k x2 |
||||||||
2 m |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда классические границы движения определяются из условия обращения скорости в нуль, а нормированное распределение вероятности имеет вид ([1-3]):
|
2 E |
1 |
|
|
|
|
x |
2 − 0.5 |
|||
a = |
|
|
|
|
|
|
|
|
|
|
|
|
pcl(x ,a) := π a |
1 |
− |
a |
|||||||
k |
|
|
|||||||||
13
|
|
|
|
Квантовый осциллятор |
|
|
|
|||||||
Задача на собственные значения для области |
−∞ < x < ∞ с учетом |
|||||||||||||
граничных условий и условия нормировки будет иметь вид: |
|
|
||||||||||||
|
|
|
−h2 |
d2 |
Ψ(x) |
+ k x2 |
Ψ(x) = E Ψ |
|
|
|
||||
|
|
|
2 m |
dx2 |
|
|
2 |
⌠∞ |
|
|
|
|
|
|
|
Ψ(x) = 0 |
при х = ± ∞ |
и |
Ψ(x) Ψ(x) dx = 1 . |
|
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
⌡− ∞ |
|
|
|
|
|
|
Если принять следующие значения для констант |
|
|
|
|||||||||||
|
mc2 := 0.5 938.28 106eV |
|
hc := 1.9732858 103 eV A , |
|||||||||||
то частота колебаний и энергия кванта излучения равны: |
|
|
||||||||||||
ω := |
k mc2− 1 |
ω = 2.612 × 10− 4 |
|
A− 1 |
hc ω = 0.515 |
eV |
||||||||
Решение этой задачи - волновые функции выражаются через полиномы |
||||||||||||||
Эрмита H(n,ξ) |
(см. [1-3]) , |
|
|
|
|
|
|
|
|
|
||||
|
b = |
h |
|
|
|
b := |
|
hc |
|
b = 0.127 |
|
A |
||
|
m ω |
|
|
|
|
mc2 ω |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ψ(n ,x ,β) := |
|
|
1 |
Her n , x |
|
−0.5 x |
2 |
||||||
|
|
|
exp |
|
, |
|||||||||
|
|
|
|
2 |
n |
n! |
π β |
|
|
β |
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
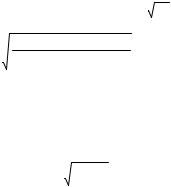
Ψ(0,x,b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ(1,x,b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ(2,x,b) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ(3,x,b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
0.5 |
|
|
0 |
|
|
0.5 |
|
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Рис. 1. Волновые функции гармонического осциллятора |
|||||||||||||
14

а спектр энергий имеет вид: |
En(n) := hc ω (n + 0.5) |
|||||||
Для представления спектра подготовим массив вспомогательных данных |
||||||||
и построим первые пять уровней. |
|
|
|
|||||
q := 0 .. 4 |
|
|
xnq := root(U(x) − En(q) ,x ,0 ,1) |
|
||||
Es0,q := En(q) |
|
Es1,q := En(q) |
Xs0,q := −xnq |
Xs1,q := xnq |
||||
|
|
|
2.5 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
U(x) |
|
1.5 |
|
|
|
|
|
|
Es |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
0 |
0.5 |
|
0 |
|
0.5 |
|
|
|
|
|
|
x,Xs |
|
|
|
|
|
Рис. 2. |
Спектр энергий осциллятора |
||||
Сопоставим классическое и квантовое распределения вероятностей. |
||||||||
Для выбранного значения n = 10 вычислим энергию состояния и оценим |
||||||||
соответствующие граничные точки поворота. |
|
|
||||||
En(10) = 5.411 |
eV |
ao := |
2 En(10) k− 1 |
|||||
Ψ(10,x,b)2 |
4 |
|
|
− ao |
|
ao |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
pcl(x,ao) |
|
|
|
|
|
|
|
|
Ψ(0,x,b)2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
0.5 |
0 |
0.5 |
1 |
|
|
|
|
|
|
x |
|
|
Рис. 3. |
Классическое и квантовое распределение вероятности |
|||||||
для состояния с n = 10 и основного состояния осциллятора |
||||||||
|
|
|
|
|
15 |
|
|
|

Дисперсии и произведение неопределенностей
Выпишем в явном виде волновую функцию основного состояния осциллятора. Она имеет вид гауссовской функции распределения.
Ψ0(x ,β) := |
1 |
|
−1 |
x |
2 |
exp |
|
||||
|
β π |
2 |
β |
|
|
Поскольку средние значения координаты и импульса равны нулю, то дисперсии координат и импульсов равны средним квадратам соответствующих величин основного состояния осциллятора. Используя символьный процессор, находим интегралы:
⌠∞ |
x2 Ψ0(x ,β)2 dx assume ,β > 0 → |
1 |
β2 |
|||||||
Dx(β) := |
||||||||||
2 |
||||||||||
⌡ |
|
|
|
|
|
|
|
|
||
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
⌠∞ |
|
|
|
2 |
|
|
|
|
|
|
|
|
d |
|
|
|
|
|||
Dp(h ,β) := −h2 Ψ0(x ,β) |
|
|
Ψ0(x ,β) dx |
|
||||||
|
|
|
|
|||||||
|
|
|
|
dx2 |
|
|
|
|||
|
⌡− ∞ |
|
|
|
|
|
|
|
|
|
Dp(h ,β) assume,β > 0 |
→ |
1 |
h2 |
|
|
|||||
|
|
|
||||||||
|
|
2 |
β2 |
|
|
|||||
Произведение неопределенностей для основного состояния осциллятора соответствует минимально возможному значению в неравенстве Гей-
зенберга.
Dx(β) Dp(h ,β) assume,β > 0 → 14 h2
или |
1 |
|
2 |
Dx Dp = 4 |
h |
|
|
|
|
Матричные элементы
По определению, матричные элементы оператора координаты равны:
⌠∞
<n | X | m> = Ψ(n ,x ,b) x Ψ(m,x ,b) dx
⌡− ∞
Вычислим эти интегралы для нескольких низших состояний с точностью
порядка 10-14. |
|
TOL := 10− 14 |
n := 0 .. 5 |
m := 0 .. 5 |
16

X |
|
|
⌠∞ |
|
,m |
:= |
|||
|
n |
|
⌡ |
|
|
|
|
|
− ∞ |
|
|
0 |
|
0.09 |
|
|
0.09 |
0 |
|
|
|
0 |
|
0.127 |
X = |
|
|
||
|
0 |
|
0 |
|
|
|
|||
|
|
|
||
|
|
0 |
|
0 |
|
|
0 |
|
0 |
Ψ(n ,x ,b) x Ψ(m,x ,b) dx |
|
|||
0 |
0 |
0 |
0 |
|
0.127 |
0 |
0 |
0 |
|
0 |
0.155 |
0 |
0 |
|
|
||||
0.155 |
0 |
0.179 |
0 |
|
|
||||
0 |
0.179 |
0 |
0.201 |
|
0 |
0 |
0.201 |
0 |
|
Сопоставим этот результат с предложенным в условии задачи, который вычислим с помощью следующей функции.
Xx(n) := |
b |
|
|
|
for p 0 .. n − 1 |
|
|
|
|||||
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
xxp,p+1 ← p + 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xxp+1,p ← p + 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
0.09 |
0 |
0 |
0 |
|
0 |
|
||||
|
|
0.09 |
0 |
0.127 |
0 |
0 |
|
0 |
|
||||
|
|
0 |
0.127 |
0 |
0.155 |
0 |
|
0 |
|
||||
Xx(5) = |
|
|
|
||||||||||
|
0 |
0 |
0.155 |
0 |
0.179 |
|
0 |
|
|||||
|
|
||||||||||||
|
|
|
|
||||||||||
|
|
0 |
0 |
0 |
0.179 |
0 |
0.201 |
|
|||||
|
|
0 |
0 |
0 |
0 |
0.201 |
|
0 |
|
||||
Полученный результат подтверждает известные правила отбора [1,3] для спектральных линий излучения гармонического осциллятора. В дипольном приближении допустимые переходы определяются условием:
n = ± 1
Упражнения
1. Вывести приведенные выше формулы для классических границ движения и плотности вероятности. Проверить условие нормировки.
17

2. Используя возможности символьного процессора MathCAD и формулу Родрига (см.[3]),
|
(ξ) |
− |
n |
|
(ξ2) dn ( |
|
(−ξ2)) |
||
H |
|
= ( 1) |
|
exp |
|
|
|
exp |
|
|
|
|
dξn |
|
|||||
n |
|
|
|
|
|
|
|
||
получить в явном виде аналитические выражения для первых пяти полиномов Эрмита. Проверить рекурентные соотношения для полиномов Эрмита. Какими свойствами четности обладают эти полиномы?
ξ Hn (ξ) = n Hn−1 (ξ) + 12 Hn+1(ξ)
3.Проверить ортогональность волновых функций гармонического осциллятора и найти нормировочную постоянную
C |
n |
= (2n n! π β)− 0.5 |
|
|
4. Найти для квантового осциллятора в состоянии с произвольным n вероятность пребывания вне классических границ движения.
5.Показать, что средние значения координаты и импульса для квантового осциллятора в любом состоянии равны нулю.
6.Вычислить среднее значение кинетической и потенциальной энергии в состоянии с произвольным n. Доказать теорему вириала:
T = U = h2ω n + 12
7.Вычислить произведение неопределенностей координат и импульсов для гармонического осциллятора в состоянии с произвольным n.
8.Используя рекурентные соотношения для полиномов Эрмита проверить, что волновые функции гармонического осциллятора удовлетворяют следующим соотношениям ([1-3]):
|
n |
ψn−1(x) + |
n + 1 |
|
x ψn(x) = b |
2 |
2 |
ψn+1(x) |
|
|
|
|
h |
|
d |
|
n |
|
n + 1 |
|
||
i |
|
|
|
ψn (x) = −i m ω b |
2 |
ψn−1(x) − |
2 |
ψn+1(x) |
|
dx |
|||||||||
|
|
|
|
||||||
9. Получить связь матричных элементов операторов координаты и им-
пульса
Pn−1,n = −i m ω Xn−1,n Pn+1,n = i m ω Xn+1,n
10. Найти собственные значения гамильтониана для одномерного уравнения Шредингера с потенциалом U(x) = mω2x2/2 при x > 0 и U(x) = ∞
при x < 0.
18
Жесткий ротатор Задача 4
Пусть частица массой m свободно движется по поверхности сферы радиуса a. Используя решение уравнения Шредингера найти: а) явный вид первых сферических гармоник; б) проверить их условие нормировки; в) зависимость плотности вероятности обнаружения частицы на поверхности сферы и построить пространственные изображения плотности вероятности в некоторых состояниях; г) вычислить частоты ротационного спектра молекулы водорода.
Решение
Сферические функции
Поскольку в центрально симметричном поле операторы квадрата момента импульса и его проекции коммутируют с гамильтонианом, то сферические гармоники являются общим набором собственных функций этих трех операторов и удовлетворяют уравнениям (см.[1-3]):
L2 Yl,m (θ,φ) = h2 l (l+1) Yl,m (θ,φ) Lz Yl,m (θ,φ) = hm Yl,m (θ,φ)
В явном виде нормированные сферические гармоники (шаровые функции) выражаются через присоединенные полиномы Лежандра. Следуя [3], представим эти зависимости с помощью встроенных функций и операторов MathCAD. Здесь и далее 0 ≤ L ≤ 5 и −L ≤ m ≤ L -
квантовые числа модуля момента и его проекции на ось Z.
am(m) := if |
|
0 ,(−1) |
m |
|
|
|
|
|
i := −1 |
|||
m < |
|
,1 |
|
|
|
|||||||
C(L,m) := |
(2 L + 1) (L − |
|
m |
|
)! |
|||||||
|
|
|||||||||||
|
4 π (L + |
|
m |
|
)! |
|||||||
|
|
|
||||||||||
|
|
|
|
|||||||||
Полиномы и присоединенные полиномы Лежандра имеют вид:
|
1 |
|
|
L |
(x2 − 1) |
L |
|
||
P(L,x) := if L = 0 ,1 , |
|
d |
|
|
|
|
, |
||
|
L |
|
dx |
L |
|
|
|
||
|
2 L! |
|
|
|
|
|
|
||
|
|
|
m |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Pm(L,m,x) := if |
m = 0 ,P(L,x) ,( |
1 − x2) |
|
|
d |
|
|
|
|
P(L,x) |
|
, |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где вместо x следует сделать замену x = cos(θ).
19
Сферические гармоники определяются соотношениями:
Y(L,m,x ,φ) := am(m) C(L,m) Pm(L,m,x) exp(i m φ) (1)
В качестве примера найдем явный вид функции Y1,1 (θ,φ). Для этого сделаем подстановку x =cos(θ) и укажем явно значение функции csgn(z).
substitute,x = cos(θ) Y(1 ,1 ,x ,φ) simplify
substitute,csgn(sin(θ))
или Y1,1 (θ,φ) =
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
2 2 |
|
sin(θ) exp(i φ) |
|||||
|
|
|
|
|
||||||||
|
→ |
3 2 |
|
|||||||||
= 1 |
4 |
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
π 2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
3 |
( |
θ |
) |
exp |
( |
i φ |
) |
|
||||
8 π |
sin |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормировка сферических функций
Условие нормировки представляется как интеграл от произведения сопряженной (SHIFT+") и прямой сферических функций в пределах полного телесного угла (см.[2]).
|
|
⌠ |
( |
|
|
( |
θ |
) |
,φ |
) |
( |
|
|
|
( |
θ |
) |
,φ |
) |
dΩ = 1 |
|
||||
|
|
|
Y L,m,cos |
|
|
Y L,m |
,cos |
|
|
|
|||||||||||||||
|
|
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, для L = 3 и m = 2 получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
⌠π |
⌠ |
2π |
( |
( |
) |
|
) |
|
( |
|
|
( |
) |
|
) |
|
|
|
( |
|
) |
dφ dθ = 1 |
, |
||
|
|
Y 3 ,2 |
,cos θ |
|
,φ |
Y 3 |
,2 ,cos |
θ |
|
,φ |
sin |
θ |
|
||||||||||||
⌡0 |
⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или, |
с учетом замены переменных x = cos(θ) |
|
|||||||||||||||||||||
|
|
|
⌠1 |
⌠2π |
|
( |
|
|
|
|
) |
( |
|
|
,x ,φ |
) |
dφ dx = 1 |
|
|||||||
|
|
|
|
Y 3 ,2 ,x |
,φ |
Y 3 ,2 |
|
|
|||||||||||||||||
|
|
|
⌡− 1 ⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сферические функции являются ортонормированной системой.
⌠
Y(L1,m1,cos(θ),φ)Y(L,m,cos(θ),φ)dΩ = δ(L1,L) δ(m1,m)
⌡
и удовлетворяют теореме сложения, где α - угол между (θ,φ) и (θ1,φ1).
L |
( |
( |
|
) |
|
) |
|
2L + 1 |
( |
( |
)) |
∑ |
|
|
= |
||||||||
Y(L,m,cos(θ1),φ1)Y L,m,cos |
θ |
|
,φ |
|
4 π |
P L,cos α |
|
||||
m = − L |
|
|
|
|
|
|
|
|
|
|
|
20
