
QuantMech_Chem_p3_85
.pdfВычислим аналитически интегралы, входящие в определение средних значений.
|
⌠∞ |
2 |
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Tr(a) := ⌡0 |
R(r,a) r |
r(r,R(r,a)) dr assume,a > 0 → |
45 a2 |
||||||||
|
|
⌠∞ |
2 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Tωr(a) := |
⌡0 R(r,a) |
dr assume,a > 0 → |
135 a2 |
|
|
||||||
⌠π ⌠2 π |
Y(θ,φ) Λ(θ,φ,Y(θ,φ)) sin(θ)dφ dθ simplify → −6 |
||||||||||
Tω := |
|
||||||||||
⌡0 |
⌡0 |
|
|
|
|
|
|
|
|
|
|
T(h ,μ ,a) := −h2 (Tr(a) + Tωr(a) Tω) → |
|
1 |
|
h2 |
|
|
|
||||
18 |
μ a2 |
|
|
||||||||
|
|
2 μ |
|
|
|
|
|||||
Принимая во внимание выражение для потенциальной энергии электрона в поле ядра, где e2 - квадрат заряда электрона, находим
|
⌠ |
∞ |
|
2 |
|
−e2 |
|
|
−1 |
|
U(a,e2) := |
|
2 |
R(r,a) |
|
dr assume,a > 0 → |
e2 |
||||
|
r |
|
r |
|
|
|||||
|
9 a |
|||||||||
|
⌡0 |
|
|
|
|
|
|
|
|
|
или, заменяя первый боровский радиус через фундаментальные постоянные, получим для потенциальной и кинетической энергий
|
|
h2 |
|
|
−1 |
|
2 |
, |
||||
U(a,e2) substitute,a = μ e2 |
→ |
9 h2 |
μ e2 |
|||||||||
|
||||||||||||
T(h ,μ ,a) substitute,a = |
|
h2 |
|
→ |
1 |
μ e22 |
|
|||||
|
μ e2 |
18 h2 |
|
|||||||||
|
|
|
|
|
|
|
||||||
И, наконец, для полной энергии, находим
T(h ,μ ,a) + U(a,e2) substitute,a = |
h2 |
→ |
−1 |
μ e22 , |
|
|
|
|
|||
|
μ e2 |
|
18 h2 |
||
что для уровня с n = 3 совпадает с хорошо известным результатом [1-8]
E(n) = |
−μ e4 |
|
2 h2 n2
31
Упражнения
1. Используя описанную выше процедуру, получить в явном виде таблицу радиальных волновых функций для 0 < n < 4 и L = 0 ... n -1.
2. Проверить условие ортогональности радиальных волновых функций.
⌠∞
r2 R(n ,L ,r)R(n ,L,r) dr = δn1,n δ( , )
1 1 L1 L
⌡0
3. Составить таблицу вещественных волновых функций водородоподобного атома для 0 < n < 4 используя процедуру, описанную в заданиях №4 и 5 данного пособия. Сопоставить с таблицей из ([8,c.39],[10,c.149]).
4. Найти наиболее вероятные значения расстояния электрона от ядра в
состояниях 1s, 2p, 3d, 4f, 5g. Показать, что эти значения удовлетворяют |
|||
соотношению |
= r1 k2 |
, |
где k = 1 ,2...5 |
r |
|||
k |
|
|
|
5. Показать, что среднее расстояние между электроном и ядром для различных состояний водородоподобного атома определяется соотношением
r |
= r1 |
n2 |
3 |
− L (L + 1) |
|||
n,L |
|
Z |
|
2 |
2 n |
2 |
|
|
|
|
|
|
|
|
|
6. Показать, что в состоянии c квантовыми числами n и L средние
значения |
(1/r) |
и (1/r)2 соответственно равны: |
|
|
|
|
||||||||
(r− 1) |
n,L |
= |
|
Z |
|
n− 2 |
(r− 2) |
n,L |
= |
|
Z |
2 |
n− 3 |
|
|
|
(L + 0.5) |
||||||||||||
|
|
r1 |
|
|
|
r1 |
||||||||
7. Убедиться в том, что в состоянии c квантовыми числами n и L > 0 средние значения (1/r)3 соответственно равны:
(r− 3) |
n,L |
= |
|
Z |
3 |
n− 3 |
|
(L + 0.5) L (L + 1) |
|||||
|
|
r1 |
||||
8. Найти распределение потенциала в атоме водорода в 1s состоянии, решая уравнение Пуассона в сферических переменных.
ΔΦ = −4π ρ(r)
9. Показать интегрированием, что в атоме Н взаимно ортогональны орбитали, например: 1) 1s и 2s; 2) 2s и 2pz; 3) 2px и 2py; 4) 3dxz и 3dxy.
32
Гибридизация атомных орбиталей Задача 6
Используя 2s - и 2p - орбитали атома H построить гибридные sp-, sp2- и sp3 - орбитали. Построить поверхностные графики и карты линий уровня в плоскости XOY. Для sp3 - орбиталей рассчитать и построить полярную диаграмму распределения плотности вероятностей на сфере выбранного радиуса.
Решение
Диагональные орбитали
Если расстояния измеряются в единицах r1 = 0.529 А , то водородные 2s- и 2px - орбитали в плоскости XOY ( z=0) в декартовых координатах:
C := |
|
1 |
r(x ,y) := |
x2 + y2 |
Px(x ,y) := |
|||
4 |
2 π |
|||||||
|
|
|
|
−r(x , |
||||
|
|
|
S(x ,y) := |
C (2 − r(x ,y)) exp |
||||
|
|
|
|
2 |
||||
|
|
|
|
|
|
|||
Гибридные орбитали диагонального типа можно
и 2px - орбиталей атома H по правилу (см.[8,10,11]):
di1(x ,y) := 1 (S(x ,y) + Px(x ,y)) |
di2(x ,y) := 1 |
2 |
2 |
−r(x ,y) C x exp 2 y)
построить из 2s -
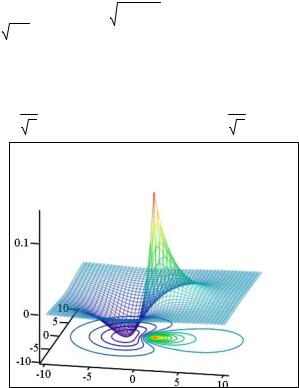
(S(x ,y) − Px(x ,y))
di1 ,di1
Рис 1. Поверхностный и контурный графики орбитали di1. Она направлена вдоль оси ОХ и ее максимум сдвинут вправо по оси.
33
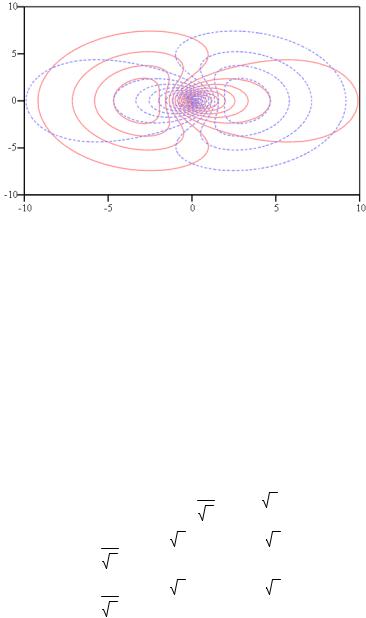
di1 ,di2
Рис 2. Контурные карты орбиталей di1 и di2
Орбиталь di2 направлена влево по оси ОХ и ее максимум тоже смещен влево от начала координат. Для линейной симметричной группировки атомов ABA диагональные гибридные орбитали на атоме B обеспечат большую электронную плотность на связи AB, чем обычные орбитали.
Тригональные орбитали
Переопределим 2s - и 2p - орбитали атома H в сферических переменных.
S(r) := C (2 − r) exp |
−r |
|
|
|
Px |
( |
r,θ,φ |
) |
:= |
|
|
|
|
( |
|
) |
|
( |
|
|
) |
exp |
−r |
|
||||||||||||||||||
2 |
|
|
|
|
|
C r sin θ |
|
cos φ |
|
|
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Py |
( |
r,θ,φ |
) |
|
|
|
( |
) |
( |
) |
exp |
−r |
|
|
( |
r |
,θ |
) |
|
|
|
|
|
|
|
( |
|
) |
exp |
−r |
||||||||||||
|
|
:= C r sin |
θ |
|
sin φ |
|
2 |
|
Pz |
|
:= C r cos θ |
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
и определим гибридные sp2 - (тригональные) орбитали tr1, tr2, tr3 на |
|
|||||||||||||||||||||||||||||||||||||||||
плоскости XOY |
(θ = π/2) по правилу (см.[8,10,11]): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
θ := |
π |
|
|
|
( |
|
|
) |
:= |
|
1 |
(S(r) |
+ |
|
2 Px |
( |
r,θ,φ |
) |
) |
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
tr1 r,φ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
( |
|
) |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
( |
|
|
|
) |
|
|
6 |
|
|
|
|
( |
|
|
|
) |
|
|
|
|||
|
|
|
|
|
:= |
|
|
S(r) |
− |
|
|
Px |
r,θ,φ |
+ |
|
|
|
Py |
r,θ,φ |
|
|
|
||||||||||||||||||||
|
|
tr2 r,φ |
|
3 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
( |
|
) |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
( |
|
|
|
) |
|
|
6 |
|
|
|
|
( |
|
|
|
) |
|
|
|
|||
|
|
|
|
|
:= |
|
|
S(r) |
− |
|
|
Px |
r,θ,φ |
− |
|
|
|
Py |
r,θ,φ |
|
|
|
||||||||||||||||||||
|
|
tr3 r,φ |
|
3 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
34
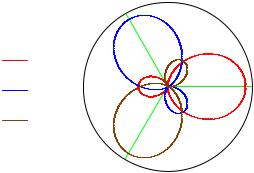
Распределение плотности вероятностей на сфере радиуса |
r := 1.5 |
|
120 |
|
|
0.004 |
|
|
tr1(r,φ)2 |
|
|
0.002 |
|
|
tr2(r,φ)2 |
0 |
|
0 |
|
|
tr3(r,φ)2 |
|
|
240
φ
Рис 3. Полярные диаграммы орбиталей tr1, tr2, tr3
Как видно из рисунка, tr1-орбиталь ориентирована вдоль оси X. Принимая во внимание сходство di1 и tr1орбиталей, можно предположить, что область положительных значений волновой функции расположена справа от центра, а tr2 и tr3орбитали областями положительных значе-
ний развернуты относительно ОX на угол 120 0 в разные стороны.
Тетрагональные орбитали
Гибридные орбитали тетрагонального типа можно построить из 2s - и 2px - орбиталей атома H по правилу (см.[8,10,11]):
te1(r,θ,φ) := 12 (S(r) + Px(r,θ,φ) + Py(r,θ,φ) + Pz(r,θ)) te2(r,θ,φ) := 12 (S(r) + Px(r,θ,φ) − Py(r,θ,φ) − Pz(r,θ)) te3(r,θ,φ) := 12 (S(r) − Px(r,θ,φ) + Py(r,θ,φ) − Pz(r,θ)) te4(r,θ,φ) := 12 (S(r) − Px(r,θ,φ) − Py(r,θ,φ) + Pz(r,θ))
Покажем, что гибридные орбитали имеют максимумы, смещенные в направлении векторов, ориентация которых в декартовой системе координат определена коэффициентами при атомных орбиталях p x , py и pz.
35
Выберем сферу радиусом порядка 1.5 r 1. Тогда плотность вероятности для каждой te - орбитали пропорциональна длине радиус-вектора в направлении углов θ и φ .
r := 1.5
f1(θ,φ) := (te1(r,θ,φ))2
x1(θ,φ) := f1(θ,φ) sin(θ) cos(φ) f2(θ,φ) := (te2(r,θ,φ))2
x2(θ,φ) := f2(θ,φ) sin(θ) cos(φ) f3(θ,φ) := (te3(r,θ,φ))2
x3(θ,φ) := f3(θ,φ) sin(θ) cos(φ) f4(θ,φ) := (te4(r,θ,φ))2
x4(θ,φ) := f4(θ,φ) sin(θ) cos(φ)
z1(θ,φ) := f1(θ,φ) cos(θ) y1(θ,φ) := f1(θ,φ)sin(θ) sin(φ) z2(θ,φ) := f2(θ,φ) cos(θ) y2(θ,φ) := f2(θ,φ)sin(θ) sin(φ) z3(θ,φ) := f3(θ,φ) cos(θ) y3(θ,φ) := f3(θ,φ)sin(θ) sin(φ) z4(θ,φ) := f4(θ,φ) cos(θ) y4(θ,φ) := f4(θ,φ)sin(θ) sin(φ)
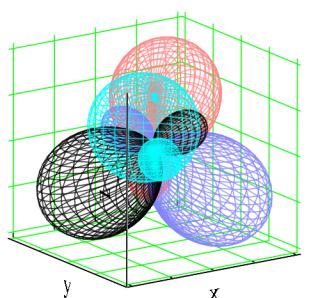
(x1,y1,z1) ,(x2,y2,z2) ,(x3,y3,z3) ,(x4,y4,z4)
Рис. 4. Плотность вероятности для te-орбиталей на сфере
36

Ортонормированность гибридных орбиталей легко проверить, если учесть ортонормированность атомных орбиталей. Например,
< tr2 | tr3 > = 13 {< S | S > + 12 < Px | Px > - 32 < Py | Py >}= 0
Упражнения
1.Проверить интегрированием в сферических переменных, что орбитали di1 и di2 нормированы и ортогональны.
2.Построить поверхностные графики орбиталей di1 и di2 на одном рисунке. Оценить взаимное расположение и характерные размеры областей положительных и отрицательных значений волновых функций.
3.Проанализировать свойства симметрии диагональных гибридных орбиталей. Как изменяются формы и свойства симметрии гибридных орбиталей при комбинировании (2s и 2 py) или (2s и 2pz ) орбиталей?
4.Построить две гибридные диагональные орбитали, которые были бы эквивалентны относительно центра симметрии, совмещенного с атомом, плоскости симметрии, перпендикулярной оси Х или оси симметрии второго порядка, также перпендикулярной оси Х (см. [11,c.258] ).
5.Построить контурные карты тригональных орбиталей в плоскости XOY. Используя контурные карты и детализируя описание, вычислить положение линии узлов для каждой орбитали.
6.Построить поверхности волновых функций тригональных орбиталей в плоскости XOY и анализируя расположение областей положительных и отрицательных значений волновых функций, убедиться, что sp2 -орби- тали лежат в этой плоскости и направлены под углом 120 0 друг к другу. Вычислить весовые коэффициенты, с которыми s- и p -орбитали входят в линейную комбинацию.
7.Проверить интегрированием ортонормированность sp2 - гибридных орбиталей.
8.Построить три гибридные тригональные орбитали на одном центре, симметричные относительно оси третьего порядка и плоскости, перпендикулярной к ней (см. [11,c.260] ).
9.Проверить интегрированием ортонормированность sp3 - гибридных орбиталей. Вычислить угол между двумя любыми sp3- орбиталями.
10.Построить четыре гибридные тетрагональные орбитали на одном центре, ортонормированные и эквивалентные в вершинах куба (см.[11] ).
11.Как и почему зависит форма "гантелек " плотности вероятности от выбора радиуса сферы, на которой они рассчитываются?
37
Орбитальные и спиновые моменты Задача 7
В стандартном {J2,Jz} представлении выписать матрицы операторов момента J2, Jz , J+ , J_ , Jx , Jy . Построить проектор и найти коэффициенты разложения состояний по выбранному базису. Вычислить среднее значение < 1 0 | Jx2 | 1 0 >. Найти собственные значения и собственные функции оператора проекции спина S x . Указать вид оператора проекции спина на произвольное направление.
Решение
Матрицы операторов момента
Оператор квадрата момента J2 и его проекции Jz коммутируют между собой. Выберем в качестве базиса в (2j+1)- мерном пространстве набор их общих собственных функций. В таком базисе (в собственном представлении) эти операторы должны быть диагональны (h = 1):
J2 | j m > = j (j+1) | j m > −j ≤ m ≤ j Jz | j m > = m | j m >
Матричные элементы повышающих J+ и понижающих J_ операторов имеют вид (см. [1,2,4,5,6,12]) , где m и j - целые или полуцелые числа.
< j m | J+ | j m -1 > = |
( j + m) ( j − m + 1) |
||||||||||
< j m | J_ | j m +1 > = |
( j − m) ( j + m + 1) |
||||||||||
Задавая в явном виде операторы Jz , J+ и J_ , получаем: |
|||||||||||
i := −1 |
|
|
|
Jz( j) := |
|
|
|
for |
m j .. −j |
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
zj−m, j−m ← m |
|
|
|
|
|
|
|
|
|
|
|
z |
|
Jp( j) := |
|
|
|
|
|
for m j .. −j |
|
||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
zj−m, j−m+1 ← ( j + m) ( j − m + 1) |
|||||
|
|
|
|
|
|
z ← submatrix(z,0 ,2 j,0 ,2 j) |
|||||
Jm( j) := |
|
|
|
for m j .. −j |
|||||||
|
|
||||||||||
|
|
|
|
|
|
zj−m+1, j−m ← ( j − m + 1) ( j + m) |
|||||
|
|
|
|
|
|
z ← submatrix(z,0 ,2 j ,0 ,2 j) |
|||||
38
Jx( j) := |
1 (Jp( j) + Jm( j)) |
|
Jy( j) := |
i |
(Jm( j) − Jp( j)) |
|
|
||||||||||||||
|
2 |
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J2( j) := Jx( j)2 + Jy( j)2 + Jz( j)2 |
1 |
0 |
0 |
|
|
|
|
|
2 |
0 |
0 |
||||||||||
При j = 1 матрицы равны: |
|
Jz(1) = 0 |
0 |
0 |
|
J2(1) = |
0 |
2 |
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
−1 |
|
|
|
|
0 0 2 |
|||||
|
0 |
1.414 |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
0 |
||
Jp(1) = |
0 |
0 |
|
|
1.414 |
|
|
|
|
Jm(1) = |
|
1.414 |
0 |
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
1.414 |
0 |
||
|
|
0 |
|
0.707 |
|
0 |
|
|
|
|
0 |
|
−0.707i |
0 |
|
||||||
Jx(1) = |
0.707 |
0 |
0.707 |
|
Jy(1) = 0.707i |
|
0 |
|
−0.707i |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0.707 |
|
0 |
|
|
|
|
0 |
|
0.707i |
|
0 |
|
|||||
|
|
|
|
Проектор и разложение единицы |
|
|
|
|
|
|
|
||||||||||
Определим кет | j m > |
и бра < j m | векторы c помощью следующих |
||||||||||||||||||||
соотношений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ket( j ,m) := |
for |
k j .. −j |
|
k = m |
|
bra( j,m) := ket( j,m)T |
|
||||||||||||||
|
|
|
|
|
zj−k ← 1 |
if |
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
zj−k ← 0 |
otherwise |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ket(1 ,−1) = |
|
0 |
|
|
|
|||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
Проверим, например, для состояния | 1 −1 >. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
bra(1 ,−1) = ( 0 |
0 |
1 ) |
|
bra(1 ,−1) ket(1 ,−1) = 1 |
|
|
|
|
|
|
|
||||||||||
Проектор на базисное состояние | j m > oпределим следующим соотношением
Pm( j,m) := ket( j,m) bra( j,m)
Найдем проекцию, например, состояний кет- 0.5 | 1 1 > + 2.5 | 1 −1 >
и брa- 0.5 < 1 1| −2.5 < 1 −1 | на базисный вектор | 1 −1 > .
0
Pm(1 ,−1) (0.5 ket(1 ,1) + 2.5 ket(1 ,−1)) = 0
2.5
(0.5 bra(1 ,1) − 2.5 bra(1 ,−1)) Pm(1 ,−1) = ( 0 0 −2.5 )
39
Используя проектор на каждое базисное состояние, можно построить единичный оператор I(j) как сумму всех проекторов (разложение единицы). При j = 1 он имеет вид:
j |
|
1 |
0 |
0 |
I( j) := ∑ ket( j,m) bra( j,m) |
I(1) = |
|
|
|
0 |
1 |
0 |
||
m = − j |
|
0 |
0 |
1 |
В качестве примера вычислим коэффициенты разложения вектора
Jx(1)Jy(1) | 1 1 > |
0.5i |
|
Jx(1) Jy(1) ket(1 ,1) = |
0 |
|
|
|
|
|
0.5i |
|
Отсюда ясно, что вектор Jx(1)Jy(1) | 1 1 > можно представить в виде:
Jx(1)Jy(1) | 1 1 > = 0.5 i | 1 1 > + 0.5 i | 1 −1 >.
Найдем среднее значение <1 0 | Jx2 |1 0 > в состоянии | 1 0 >. bra(1 ,0) Jx(1)2 ket(1 ,0) = 1
Спин s = 1/2
Задача на собственные значения для оператора Sx проекции спина на
ось X (как и ранее, в {J2,Jz }- представлении) может быть записана в форме
Sx Ψsx = sx Ψsx или Sx |s,sx> = sx |s,sx> ,
где матрица оператора Sx выражается через матрицу Паули (см.[1,2,5,6]) и волновая функция Ψsx = |s, sx > имеет вид:
|
1 |
0 |
1 |
, |
|
a |
, |
||
Sx := |
|
|
1 |
|
Ψsx = |
b |
|||
2 |
|||||||||
|
|
0 |
|
|
|
||||
а коэффициенты a и b должны удовлетворять условию нормировки
a2 + b2 = 1
Отсюда получается однородная система уравнений a = 2sx b , b = 2sx a .
Она разрешима при условии 4 sx2 = 1, что дает sx = -1/2 и sx = 1/2. В MathCAD собственные значения и соответствующие им векторы
легко находятся: |
|
|
−0.5 |
|
|
eigenvals(Sx) = |
|||
|
0.5 |
|
||
|
|
|||
40
