QuantMech_Chem_p3_85

Поэтому для основного (невырожденного) состояния эффект Штарка первого порядка отсутствует. Рассмотрим первое возбужденное (n = 2) состояние. Оно четырехкратно вырожденно. Нормированные волновые функции для разных значений орбитального момента | 2lm > имеют вид:

Оператор возмущения V является нечетным относительно отражения в начале координат. Поэтому отличными от нуля будут только матричные элементы для невозмущенных состояний с противоположными четно-

Пусть Eo - энергия исходного вырожденного состояния. Тогда с учетом поправок исходный уровень с n = 2 расщепляется на три разных уровня. Поскольку E пропорциональны ε , то это - линейный эффект Штарка.

61

Упражнения

1.Вычислить поправки первого и второго порядка по теории возмущений для первого возбужденного состояния осциллятора с потенциалом V(x) = a |x| . Оценить изменение частоты перехода (n=1--> n=0) для принятых выше параметров молекулы водорода и потенциала возмущения.

2.Для ангармонического осциллятора с потенциалом возмущения вида

V(α,β,x) = α x3 + β x4

проверить, что поправка первого и второго порядка к энергии n - го состояния гармонического осциллятора равна (см.[3-5])

3. Показать, что в задаче об атоме водорода в электрическом поле

функции являются гибридными (диагональными) sp - орбиталями.

4. Пространственный ротатор с моментом инерции J и дипольным моментом d, направленным вдоль оси ротатора, помещен в однородное электрическое поле ε, рассматриваемое как возмущение. Найти первые неисчезающие поправки к энергии основного уровня и показать (см[4]),

что поляризуемость основного состояния ротатора равна β = 2Jd2/3h2 .

5.В первом порядке теории возмущений найти поправку к уровням энергии водородоподобного иона при учете слагаемого -- p 4/8m3c2 в квазирелятивистской функции Гамильтона электрона в поле ядра (см[4]).

6.Cчитая, что гамильтониан спин-орбитального взаимодействия имеет

найти в первом порядке по теории возмущений энергию спин-орбиталь- ного взаимодействия Eсо = < nlm | V(r) | nlm > для водородоподобного иона. Вычислить эту энергию для электрона, находящегося на 2p-AO атома водорода (см.[4]).

7. Найти энергию основного состояния атома гелия в первом порядке теории возмущений, рассматривая взаимодействие электронов как малое возмущение. Сопоставить результат с вариационным расчетом и указать возможные причины различий (см.[3,4]).

62

Элементы теории групп и представлений групп Задача 11

Для правильного треугольника: а) указать все элементы симметрии и построить взаимно однозначное соответствие с элементоми группы перестановок ядер симметричной трехатомной молекулы; б) построить совокупность матриц третьего порядка, однозначно связанных с элементами группы перестановок и составить таблицу умножения этой группы; в) найти неприводимые представления и их характеры; г) построить базисные функции неприводимых представлений; д) найти матрицы прямого произведения представлений.

Решение

Элементы симметрии и перестановки

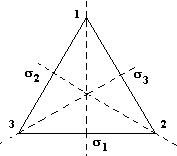
Обозначим вершины треугольника цифрами 1,2,3, а соответствующие оси симметрии буквами σ1,σ2,σ3 (Рис.1). Имеем 6 операций симметрии:

Е - единичная операция; σ1 - отражение в плоскости σ1;

σ2 - отражение в плоскости σ2; σ3 - отражение в плоскости σ3;

C3 - поворот вокруг оси, проходящей

Выполняя операции симметрии, обнаружим, что каждому элементу можно поставить в соответствие определенную перестановку индексов

Полученная группа перестановок обозначается Р3. Соответствие между элементами групп однозначно и не нарушается при выполнении опера-

63

Матрицы и таблица умножения группы S3

Сопоставим каждой вершине {1, 2, 3} треугольника вектор по правилу:

Тогда каждая операция симметрии может быть представлена матрицей. Это представление является точным. Вид матриц легко получить, анализируя их результаты действия на векторы X1, X2 и X3 и сопоставляя с операциями симметрии.

Группа не является абелевой, поскольку произведение операций сим-

Данная группа имеет следующие подгруппы: 1) тривиальная подгруппа, состоящая из единицы Е; 2) подгруппа, состоящая из элементов {E,A,B}; 3) подгруппа {E,C}; 4) подгруппа {E,D}; 5) подгруппа {E,F}. Порядки подгрупп равны 1, 3 и 2. Это соответствует теореме Лагранжа, согласно которой, порядок подгруппы конечной группы является делителем порядка группы.

Для нахождения таблицы умножения группы (квадрата Кэли) воспользуемся описанной ниже программной функцией MTable. Для ее реализации представим элементы группы симметрии как элементы одномерного символьного массива t и как элементы трехмерного массива вложенных (nested) матриц G. Функция вычисляет произведение матриц и сопоставляет его с каждым элементом группы S3 .

64

Матрицы поворотов и отражений

Построим еще одно представление группы C3v . На этот раз - двумерное как преобразование координат точки (x,y) на плоскости вокруг центра треугольника, оставляя z- координату неизменной и принимая равным единице расстояние от центра треугольника до вершины.

Такое представление состоит из матриц (2x2), вложенных в трехмерные матрицы. Их можно получать на основе матрицы преобразования координат вектора при повороте вокруг центра треугольника в плоскости, перпендикулярной оси Z, и матрицы отражений. Матрицы собственных и несобственных (с отражением в горизонтальной плоскости) вращений вектора по часовой стрелке показаны ниже (см. [7-9,14]).

65

Поворотам на 1200 и 2400 по часовой стрелке отвечают матрицы a и b. Отражения в плоскостях σ1 , σ2 и σ3 реализуются матрицей с и как комбинации d = c a и f = a c .

Ортогональность и характеры представлений

Следуя законам преобразований функции при действии на нее операторов симметрии, можно получить два одномерных представления группы C3v . Поскольку

Первое из них является полносимметричным представлением A1, а в представлении Γ2 при отражениях функция должна изменить знак (A2).

В качестве третьего представления выберем двумерное представление Γ3 типа Е, полученное выше с помошью матриц вращения и отражения.

Четвертое представление G - совокупность матриц E, A, ... F группы S 3.

66

Проверим ортогональность матричных элементов, например, для представления Γ3, выполняя суммирование по всем элементам группы. Условие ортогональности имеет вид (см. [7-9,14]):

Для унитарных вещественных матриц обратная равна транспонированной, поэтому, например, для подобных элементов условие ортогональности дает:

Эти значения равны порядку группы, деленному на размерность представления 6/2 = 3. Другие элементы представления Γ3 ортогональны, например,

В соответствии с определением, вычислим характеры представления как сумму диагональных элементов матриц, например, для представления G.

Условие ортогональности вещественных характеров имеет вид ([9,14]):

∑χα(g) χβ(g) = g δαβ g

67

Поскольку сумма квадратов характеров не равна порядку группы g = 6, то это представление является приводимым. Вычислим коэффициенты его разложения по характерам неприводимых представлений Γ1, Γ2, Γ3.

Следовательно, представление G разлагается в сумму Γ1, Γ2, Γ3 с коэффициентами m1 = 1, m2 = 0 и m3 = 1.

G = m1 A1 + m2 A2 + m3 E

Базисные функции представления

Пусть задан набор из трех одинаковых по форме функций φ1(r1) , φ2(r2), φ3(r3), значения которых зависят только от расстояния точек до вершин треугольника. Такими функциями могут быть атомные орбитали, центрированные на атомах 1, 2 и 3. Операции симметрии группы С3v переводят эти функции друг в друга. Если представить эти три функции как элементы вектор-столбца, то закон преобразования можно определить следующим образом:

68

Результаты преобразований R(g) выбранных функций φk и характеры неприводимых представлений группы C3v можно свести в таблицу.

Для конструирования базисных функций, преобразующихся по конкретным неприводимым представлениям группы воспользуемся аппаратом проекционных операторов. По определению проекционных опе-

раторов (см. [7-9,14,15])

где nα - размерность представления, g - порядок группы, R(g) - операция симметрии, Γα(g)k,i - матричный элемент транспонированной (ве-

щественной) матрицы представления Γα(g), χα(g) - ее характер, а сум-

мирование ведется по всем элементам группы. Для полносимметричного представления А1 оператор и результат проектирования имеют вид:

Предполагая ортонормированность функций φk можно получить нормированную полносимметричную функцию.

69

Для представления А2 оператор проектирования имеет вид:

PA2(Φ) := 16 χ20 E + χ21 A + χ22 B + χ23 C + χ24 D + χ25 F Φ,

а результат его действия на пробные функции свидетельствует о том, что среди выбранных функций нет базисных функций представления А2 .

Для двумерного представления Е нужно построить две ортогональные компоненты. Для этого построим проектор и подействуем им на выбранные пробные функции.

После нормировки первой и второй строки находим:

Поскольку первая и вторая строка не ортогональны, то для нахождения второй базисной функции воспользуемся процедурой ортогонализации Шмидта. В качестве ψE2 выберем функцию

ψE2 = ψ2 + CE ψE1 ,

где константа CE должна быть выбрана из условия ортогональности

⌠

ψE1 ψE2 dτ = 0

⌡

Это условие выполняется, если

70