QuantMech_Chem_p3_85

Плотность вероятности

Поскольку квадрат модуля сферической гармоники не зависит от азимутального угла φ , то величина

dP(L,m,θ) = ( Y(L,m,cos(θ),φ) )2 2 π sin(θ) dθ

соответствует вероятности обнаружить частицу на сфере постоянного радиуса в кольцевом сегменте с углами от θ до θ + dθ . Плотность вероятности равна

f(θ) = dP(L,m,θ) = ( Y(L,m,cos(θ),φ) )2

dΩ

В качестве примера построим угловую диаграмму плотности вероятности для f -состояния с L = 3 и m = 1. Для этого состояния

f(θ) := 6421π sin(θ) (5 cos(θ)2 − 1) 2

240300

θ+ π

2

Рис. 1. Полярная диаграмма f - состояния с L=3 и m=1. Начало отсчета угла θ смещено на 900 с тем, чтобы ось Z соответствовала вертикали

Принимая во внимание независимость плотности вероятности от азимутального угла φ можно представить эту функцию как поверхность вращения относительно вертикальной оси Z. Выполним разрез поверхности чтобы передать ее внутреннюю структуру.

21

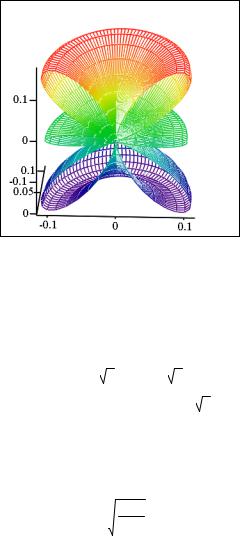
x(θ,φ) := f(θ) sin(θ) cos(φz)(θ,φ) := f(θy)(cosθ,φ(θ)):= f(θ)sin(θ) sin(φ)

S := CreateMesh(x ,y ,z,0 ,π,0 ,π,60)

S

Рис. 2. Пространственная диаграмма плотности вероятности (L=3, m=1)

При анализе распределения плотности вероятности удобнее оперировать с вещественными функциями. Благодаря вырождению по m линейная комбинация сферических функций с ненулевыми симметричными значениями m тоже является решением уравнения Шредингера. Тогда можно переопределить сферические функции для неравных нулюm, до-

множая полиномы Лежандра на 2sin(mφ) и 2cos(mφ) вместо exp(imφ). Y(L,m,x ,φ) := if (m = 0 ,C(L,m) Pm(L,m,x) , 2 C(L,m) Pm(L,m,x))

Y(L,m,x ,φ) := Y(L,m,x ,φ) if (m < 0 ,sin(m φ),cos(m φ)) (2)

Получаемые таким образом сферические функции соответствуют принятому в квантовой химии определению px -, py -, dxy -, dxz - и других атомных орбиталей. Например, для dxy - орбитали имеем [8]:

Тогда плотность вероятности dxy - орбитали - длина радиус-вектора в направлении углов θ и φ .

22

(x ,y ,z)

Рис. 3. Пространственная диаграмма плотности вероятности для dxy - орбитали. Как легко видеть, эта орбиталь имеет две взаимно перпендикулярные узловые плоскости.

Ротационный спектр молекулы водорода

Пусть межатомное расстояние в молекуле H2 , приведенная масса ее атомов и момент инерции молекулы равны:

Согласно [1-3], энергетический спектр жесткого ротатора и частота излучения для ротационных переходов определяются соотношениями:

23

Получаемое значение частоты ω(1) равно разности частот соседних переходов и примерно на порядок меньше, чем основная частота излучения колебательного спектра. Из этого видно, что чисто ротационный спектр представляет собой набор равноотстоящих друг от друга линий.

Упражнения

1. Используя предлагаемую в данной задаче процедуру расчета (определение №1) составить таблицу сферических функций для квантовых чисел L и m в диапазоне L ≤ 3 и −L ≤ m ≤ L .

2.Показать, что сферические функции являются ортонормированной системой функций.

3.В состоянии с волновой функцией Ψ(θ,φ) найти коэффициенты

разложения по сферическим функциям, допустимые значения момента импульса, его проекции на ось Z и вычислить их вероятности.

Ψ(θ,φ) = A 1 + cos(θ) + sin(θ) (exp(i φ) + exp(−i φ))

6.Построить пространственные распределения плотности вероятности для состояний, найденных в упражнении 1.

7.Используя предлагаемую в данной задаче процедуру расчета (опре-

деление №2) составить таблицу вещественных сферических функций для квантовых чисел L и m в диапазоне L ≤ 3 и −L ≤ m ≤ L . Соотнести

их с s -, pz -, py -, px -, dz2 -, dyz -, dxz -, dxy -, dx2 - dy2 и другими состояниями (см. [7,8]).

8. Построить пространственные распределения плотности вероятности для состояний, найденных в упражнении 7.

9. Вычисляя матричные элементы вида (см.[1-3]) < L1m1| cos(θ) | Lm > ,

< L1m1| sin(θ) exp(iφ) | Lm > и < L1m1| sin(θ) exp( -iφ) | Lm >

как интегралы от комплексных сферических функций проверить правила отбора по дипольным переходам для ротатора:

m = 0 , ± 1 ; L = ± 1

24

Волновые функции атома водорода Задача 5

Используя решение радиального уравнения Шредингера для атома водорода найти: а) явный вид радиальных волновых функций для некоторых состояний; б) распределение электронной плотности для этих состояний; в) построить карту изолиний волновой функции и ее квадрата модуля; г) проверить теорему вириала для 3dx2 - y2 - состояния.

Решение

Радиальное уравнение Шредингера

Электрон в атоме водорода находится в кулоновском поле ядра. Радиальное уравнение имеет вид (см.[1-3]) для области 0 < r < ∞ с учетом

Решение этой задачи на собственные значения выражается через обобщенные полиномы Лягерра, представленные формулой Родрига [1-3].

Нормированная радиальная волновая функция представляется в виде:

где n = 0, 1... ∞ , L = n - 1 -главное и орбитальное квантовые числа эле-

ктрона, Z - заряд ядра водородоподобного иона, r1первый боровский радиус и в формуле следует сделать замену переменной

ρ = 2 Z r n r1

25

Получим в явном виде радиальную функцию, например, для состояния

1s с n = 1 и L = 0.

Распределение электронной плотности

Плотность вероятности распределения заряда по радиусу в сферическом слое радиуса r и толщиной dr независимо от углов (после интегрирования по углам) равна (см.[1-3]):

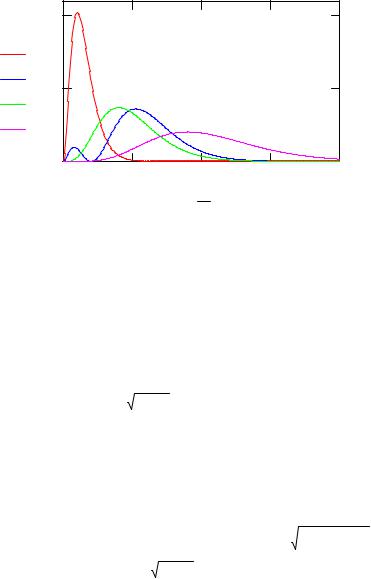
Выпишем эти функции для состояний 1s, 2s, 2p, 3d , полагая Z =1, C = 1, и поcтроим графики распределений электронной плотности.

26

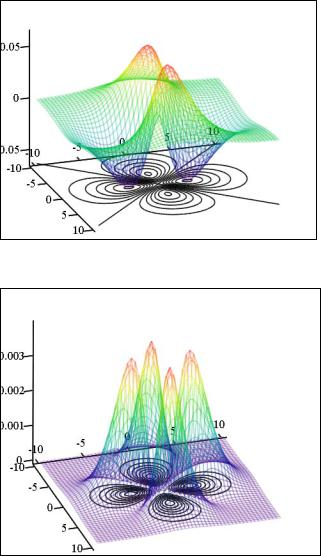
Ψ,Ψ

P,P

Рис. 2. Поверхность и изолинии волновой функции и ее квадрата модуля в плоскости X,Y для состояния c n = 3, L = 2 m = 2.

28

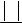
Теорема вириала

В системе с кулоновским взаимодействием ([7-8]), среднее значение кинетической энергии в стационарном состоянии с собственной волновой функцией Ψ и энергией E, равно половине модуля среднего значения потенциальной энергии, а их сумма равна полной энергии системы. Теорема вириала строго выполняется для точных решений. Отклонение от этой теоремы является одним из основных тестов для проверки точности решения.

Для вычисления средних значений кинетической и потенциальной энергий электрона в атоме водорода воспользуемся вещественными волновыми функциями в cферической системе координат в форме:

Ψ(r,θ,φ) = R(r) Y(θ,φ) ,

где радиальная и угловая части волновой функции независимо нормированы. Среднее значение потенциальной энергии с учетом условия нормировки для угловой части и элемента объема вида

⌠

Y(θ,φ)2 dΩ = 1 , dτ = r2 dΩ dr

⌡

определяется следующим соотношением

Для вычисления среднего значения кинетической энергии определим следующие операторы, реализующие радиальную, угловую часть лапласиана в сферических переменных и оператор кинетической энергии.

29

По определению, среднее значение кинетической энергии равно:

Принимая во внимание явный вид оператора кинетической энергии, представим определение среднего значения в развернутой форме.

Выделим слагаемые, относящиеся к радиальной и угловой части лапласиана.

где а - первый боровский радиус.

Проверим, как введенные операторы действуют на выбранную волновую функцию.

30