
QuantMech_Chem_p3_85
.pdf
⌠ |
|
|
−1 |
|
ψE1 ψ2 dτ = |
||
CE = − |
2 |
||
⌡ |
|
|
|
После нормировки получаем: |
ψE |
= |
1 (φ2 − φ3) |
|
|
2 |
2 |
Прямое произведение представлений
По определению прямого произведения представлений ([14,15]) можно
записать |
(Γα Γβ) |
|
= Γα |
|
Γβ |
|
|
(i, j)(kl) |
i,k |
j,l |
|||
|
|
|
|
Используя операцию векторизации на панели Matrix определим произведение одномерных представлений и убедимся, что они образуют од-
номерную подгруппу относительно произведения. |
|
|
|
|||||||||
|
→ |
|
→ |
|
→ |
|||||||
Γ1xΓ1 := (Γ1 Γ1) |
Γ1xΓ2 := (Γ1 Γ2) |
Γ2xΓ2 := (Γ2 Γ2) |
||||||||||
|
1 |
|
1 |
|
1 |
|||||||
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
Γ1xΓ1 = |
|
|
Γ1xΓ2 = |
|
|
Γ2xΓ2 = |
|
|
||||
|
1 |
|
|
−1 |
|
|
1 |
|
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
−1 |
|
|
|
1 |
|
|
|
1 |
|
−1 |
|
1 |
|||||||
Поступая аналогично, находим произведения одномерных представле-
ний Γ1 и Γ2 с двумерным представлением Γ3, например: |
|
|
|
|||||
|
→ |
|
|
|
|
|
|
|
Γ1xΓ3 := (Γ1 Γ3) |
|
|
|
{2,2} |
||||
Γ1xΓ34 = |
|
0.5 |
−0.866 |
|
|
|
{2,2} |
|
|
−0.866 |
−0.5 |
|
|
|
{2,2} |
|
|
|
Γ1xΓ3 |
= |
|
|
||||
|
→ |
|
|
|
|
|||
Γ2xΓ3 := (Γ2 Γ3) |
0.866 |
|
|
|
{2,2} |
|
||
Γ2xΓ34 = |
−0.5 |
|
|
|
{2,2} |
|
||
0.866 |
0.5 |
|
|
{2,2} |
||||
Для определения произведения двумерных представлений воспользуемся встроенными функциями augment() и stack(), а также операцией векторизации. Получаем массив вложенных матриц 4х4.
f(x ,y) := stack(augment(x0,0 y ,x0,1 y),augment(x1,0 y ,x1,1 y))
71
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{4,4} |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{4,4} |
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
{4,4} |
|
|
|
||||||||
Γ3xΓ3 := f(Γ3 ,Γ3) |
|
|
|
|
|
|
Γ3xΓ3 = |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
{4,4} |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Матрицы произведений в явном виде: |
|
|
|
|
|
|
|
{4,4} |
|
|
|
||||||||||||
|
|
|
|
|
{4,4} |
|
|
||||||||||||||||
|
|
1 |
|
|
|
0 |
|
|
|
|
0.25 |
|
|
|
|
||||||||
|
|
0 |
0 |
|
|
|
|
|
−0.433 |
−0.433 |
0.75 |
||||||||||||
Γ3xΓ30 = |
0 |
1 |
0 |
0 |
|
Γ3xΓ31 = |
0.433 |
|
0.25 |
|
−0.75 |
−0.433 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
−0.75 |
|
|
|
|
−0.433 |
|
||||||
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
0.433 |
|
|
|
0.25 |
|
||||||
|
|
0 |
0 |
0 |
1 |
|
|
|
|
0.75 |
|
0.433 |
|
0.433 |
|
0.25 |
|
||||||
|
|
|
|
0.25 |
|
0.433 |
0.433 |
0.75 |
|
|
|
1 |
0 |
0 |
0 |
|
|||||||
Γ3xΓ32 = |
−0.433 |
0.25 |
−0.75 |
0.433 |
Γ3xΓ33 = |
0 |
−1 |
0 |
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
−0.433 |
−0.75 |
0.25 |
0.433 |
|
|
|
|
|
0 |
0 |
−1 0 |
|
||||||||
|
|
|
|
0.75 |
|
−0.433 −0.433 |
0.25 |
|
|
|
0 |
0 |
0 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
0.25 |
−0.433 |
−0.433 0.75 |
|
|
|
|
|
|
|
|||||
|
|
|
|
Γ3xΓ34 = |
−0.433 |
−0.25 |
|
|
0.75 |
0.433 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
−0.433 |
0.75 |
|
−0.25 |
0.433 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0.75 |
0.433 |
|
0.433 |
0.25 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0.25 |
0.433 |
|
0.433 |
|
0.75 |
|
|
|
|
|
|
|
|||
|
|
|
|
Γ3xΓ35 = |
0.433 |
−0.25 |
|
0.75 |
|
−0.433 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0.433 |
0.75 |
|
−0.25 |
|
−0.433 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0.75 |
−0.433 |
−0.433 |
0.25 |
|
|
|
|
|
|
|
|||||
Поскольку |
|
Γ1xΓ2 = Γ2 и Γ2xΓ2 = Γ1 , то характеры этих произведений |
|||||||||||||||||||||
уже вычислены. Характеры других вариантов произведений можно |
|
||||||||||||||||||||||
найти из явного вида матриц или с помощью функции Char(). |
|
|
|
||||||||||||||||||||
( |
Γ2xΓ3 |
) |
= |
0 |
"_E_" "_A_" "_B_" "_C_" "_D_" "_F_" |
|
|||||||||||||||||
Char |
|
"Ch" |
|
2 |
−1 |
|
−1 |
|
|
0 |
0 |
|
0 |
|
|
||||||||
( |
|
|
) |
|
|
|
|
|
|
|
|||||||||||||
Γ3xΓ3 |
= |
0 |
"_E_" "_A_" "_B_" "_C_" "_D_" "_F_" |
|
|||||||||||||||||||
Char |
|
"Ch" |
|
4 |
1 |
|
1 |
|
|
0 |
0 |
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
χ |
|
|
|
( |
|
( |
|
|
) |
,1 ,1 ,1 ,6 |
)T |
|
|
|
|
||
|
|
|
|
|
|
33 := submatrix |
Char Γ3xΓ3 |
|
|
|
|
|
|
||||||||||
72
Проверим критерий приводимости (см. [7,14]) для представления Γ3xΓ3 .
5
∑i = 0 χ33i 2 = 18
Поскольку сумма квадратов характеров не равна порядку группы g = 6, то это представление является приводимым. Вычислим коэффициенты его разложения по характерам неприводимых представлений Γ1, Γ2, Γ3.
m1 := 61 |
5 |
|
m2 := 61 |
5 |
m3 := 61 |
5 |
∑ |
χ33i χ1i |
∑ χ33i χ2i |
∑ χ33i χ3i |
|||
|
i = 0 |
|
|
i = 0 |
|
i = 0 |
m1 = 1 |
|
m2 = 1 |
m3 = 1 |
|||
Следовательно, представление Γ3xΓ3 разлагается в сумму Γ1, Γ2, Γ3 с коэффициентами m1 = 1, m2 = 1 и m3 = 1.
Γ3xΓ3 = m1 A1 + m2 A2 + m3 E
Упражнения
1. Используя таблицу умножения группы S3 показать, что эта группа (и, конечно, изоморфная ей группа C3v) разбивается на три класса сопряженных элементов: 1) E; 2) C3 , C32 ; 3) σ1, σ2, σ3 .
2.Используя указанное выше разбиение группы S 3 на подгруппы построить смежные классы элементов по каждой подгруппе.
3.Изображая элементы группы C3v в виде столбца и действуя на этот столбец каждой операцией симметрии, получить регулярное представление группы. Выписать матрицы этого представления и найти его размерность. Выяснить, на какие неприводимые представления оно разбивается.
4.Проверить приведенные выше условия ортогональности и нормировки для базисных функций неприводимых представлений группы C3v .
5.Построить матрицы прямого произведения представлений G x G, найти их характеры и разложить полученное представление по неприводимым представлениям группы C3v .
6.Найти операции симметрии группы С2h. Составить таблицу группового умножения. Выделить подгруппы и классы сопряженных элементов [8,14]. Привести пример молекулы с симметрией этой группы.
73
7.Постройте прямые произведения неприводимых представлений [8,14]
группы С2h . Какие состояния взаимодействуют между собой, если возмущение обладает симметрией Au ?
8.Найти операции симметрии, порядок группы и символ группы сим-
метрии для молекул (см. [8,9,14-17]): а) H2O; б) этан; в) аллен; г) метан; д) бензол; е) нафталин; ж) антрацен; з) ацепентилен; и) циклопентадиен.
9.Найти операции симметрии молекулы C2H4. Какие водородные 1s-ор- битали преобразуются по неприводимым представлениям этой группы?
10.Найти симметризованные π -молекулярные орбитали, преобразующиеся по неприводимым представлениям группы С6v для бензола.
11.Найдите симметризованные π -молекулярные орбитали, преобразующиеся по неприводимым представлениям группы D6h для бензола.
12.Какие водородные 1s-орбитали преобразуются по неприводимым представлениям группы Td симметрии метана?
13.Получить все симметризованные π -молекулярные орбитали молекулы нафталина с симметрией группы С2v (см. [8,14]).
14.Найти операции симметрии октаэдрической молекулы SF6 .
15.Найти операции симметрии икосаэдрической молекулы С20Н20 .
16.Определите, какие группы порождаются прямым произведением групп: а) C3 x Ci ; б) C2 x Cs ; в) D2 x Cs ?
17.Вычислите характеры прямых произведений неприводимых представлений групп: а) C3 x Ci ; б) C2 x Cs ; в) D2 x Cs .
18.Вычислить характеры прямого произведения неприводимых представлений группы C4v .
19.Рассматривая произвольное вращение в пространстве как три последовательных поворота на углы Эйлера, построить матрицы этих поворотов и найти матрицу, описывающую полное вращение (см. [9,14]).
20.Рассмотрим атом щелочного металла, помещенный в поле трех точечных зарядов, образующих правильный треугольник так, что получается правильная пирамида с вершиной в данном атоме. На какие уровни распадается 2-р уровень свободного атома? Как действуют опера-
ции группы симметрии С3v на функцию f(θ,φ)? Найдите представление группы С3v , порождаемое тремя комплексными 2-р функциями.
74

Метод молекулярных орбиталей Хюккеля Задача 12
Методом молекулярных орбиталей Хюккеля (МОХ) рассчитать π− электронные энергии и коэффициенты при атомных орбиталях в молекуле бутадиена C4 H6 . Вычислить порядки связей, индексы свободной валентности и распределение электронной плотности. Используя симметрию молекулы упростить вековое уравнение.
Решение
Метод молекулярных орбиталей
Метод молекулярных орбиталей Хюккеля (МОХ)- простейший расчетный качественный метод квантовой химии, применяющийся для определения параметров плоских молекул углеводородов с сопряженными связями. Он основан на учете только π - электронов. Каждый атом углерода вносит вклад в π - связи через 2pz - атомные орбитали. Его алгоритм можно получить на основе линейного вариационного метода. Выбирая пробную функцию ψ (молекулярную орбиталь) в виде линейной комбинации атомных (слэтеровских) орбиталей φj , получаем задачу на собственные значения для гамильтониана данной системы из n π - электронов:
n−1
ψ = ∑ cj φj , j = 0
Hψ = Eψ .
В методе предполагается, что диагональные матричные элементы гамильтониана (кулоновские интегралы) постоянны и равны некоторому параметру α, а внедиагональные элементы Hj, k = β, если атомы
j и k связаны между собой ковалентной связью и равны нулю в противном случае. Матрица S интегралов перекрывания равна единичной матрице. Величины кулоновского α− и резонансного β− интегралов отрицательны. Их точные значения в методе МОХ не фиксируются, поскольку результаты зависят от отношения α и β. Соответствующее характеристическое уравнение имеет вид (см. [7-9,16-17])
H |
j,k |
− E δj,k |
= 0 |
|
|
|
Для компактной записи характеристического уравнения обычно вводят переменную x = (α -E )/β . Тогда все диагональные. элементы будут равны x , а внедиагональные - нулю или единице, в зависимости от структуры молекулы. Например, для молекулы C4 H6 (см. рис. 1)
75
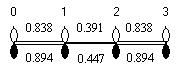
Рис. 1. Модель молекулы бутадиена C4 H6
гамильтониан можно сформировать в символьном виде, используя параметры α и β , или топологическую матрицу A(х) при х = 0.
H(α,β) := |
|
|
for |
j 0 .. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
for k 0 .. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
c |
j,k |
← if (j = k ,α,if ( |
|
j − k |
|
= 1 ,β,0)) |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hh( j,k) := |
if ( j = k ,0 ,if ( |
|
j − k |
|
= 1 ,1 ,0)) |
|
|
|
|
|
|
A := |
matrix(4 ,4 ,hh) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
α β 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 0 0 |
|||||||||
( |
|
|
) |
|
|
β α β 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 1 0 |
|
|||||||
α,β |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
|
|
|||||||||||||||
H |
|
|
0 β α β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 0 1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 0 β α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 1 0 |
|||||||||
|
|
|
|
|
|
|
|
Собственные значения энергии |
|
|
|
|
|
|
|
|
|
||||||||||||||||
Найдем символьное решение для собственных значений энергии Е |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
5 |
|
|
|
β + α |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
solve ,E |
|
|
|
− |
|
|
|
5 |
|
|
|
β + α |
|
|
|||||
|
|
H(α,β) − E identity(4) |
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
collect,β |
→ |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
5 |
β + α |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
5 |
β + α |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
76
или численное решение с использованием встроенных функций и выполняя упорядочивание расположения корней (α < 0 и β < 0 !).
|
|
1.618 |
|
|
|
|
|
0.618 |
|
λ := eigenvals(A) |
λ := reverse(sort(λ)) |
λ = |
|
|
|
|
|
−0.618 |
|
|
|
|
|
|
|
|
|
−1.618 |
|
Таким образом, упорядоченные собственные значения имеют вид:
λ := |
1 |
(1 + 5 −1 + 5 1 − 5 −1 − 5 )T |
|
2 |
|||
|
|
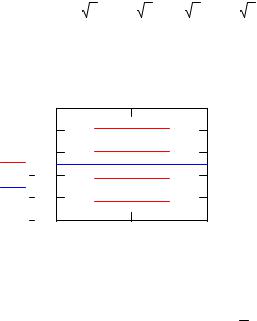
Построим диаграмму энергетических уровней бутадиена. Отметим, что занятыми в основном состоянии являются два нижних уровня (λ k > 0)
i := 0 .. 1 k := 0 .. 3 |
R |
i,k |
:= 0.25 + i 0.5 |
Λi,k := −λk |
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
1.5 |
|
|
|
|
Λ |
0.5 |
|
|
|
|
|
|
|
|
|
|
0 |
0.5 |
|
|
|
|
|
1.5 |
|
|
|
|
|
2.5 0 |
|
|
0.5 |
1 |
|
|
|
|
R,r |
|
Рис. 2. Диаграмма энергетических уровней для C4 H6 |
|||||
Суммарная энергия π - электронов равна (см. [7-9,16-17]) |
|||||
|
1 |
|
|
|
1 |
|
(α + β λk) collect,β |
|
|||
Eπ(α,β) := 2 ∑ |
→ 2 5 2 β + 4 α |
||||
k = 0
Собственные векторы
Поскольку все собственные значения различны, для вычисления всех коэффициентов молекулярных орбиталей можно использовать встроенную функцию eigenvec(), не нарушая их упорядочивания. Коэффициенты молекулярных орбиталей представлены столбцами в матрице, составленной из собственных векторов. Напомним, что собственные векторы нормированы на единицу.
77
k := 0 .. 3 |
C k := |
eigenvec(A,λk) |
||||
|
0.372 |
−0.602 |
−0.602 |
0.372 |
|
|
C = |
0.602 |
−0.372 |
0.372 |
−0.602 |
|
|
|
0.372 |
0.372 |
0.602 |
|
||
|
||||||
|
0.602 |
|
||||
|
0.372 |
0.602 |
−0.602 |
−0.372 |
|
|
В случае кратных собственных значений необходимо использовать функцию eigenvecs() и дополнительно упорядочивать векторы с последующей проверкой типа
δC k := A C k − λk C k
Порядки связей и свободная валентность
Рассчитаем порядок π-электронной связи. Пусть n1 = 2 -число занятых молекулярных орбиталей, а n2 = 2 - число электронов на каждой из занятых орбиталей (см. рис. 2). Полученные значения порядков связей совпадают с указанными на рис.1 (см. также [7-9,16-17]).
|
|
|
|
n1−1 |
n1 := 2 |
n2 := 2 |
p( j,k) := ∑ n2 Cj,i Ck,i |
||
|
|
|
|
i = 0 |
p(0 ,1) = 0.894 |
p(1 ,2) = 0.447 |
p(2 ,3) = 0.894 |
||
Плотность π - электронов у каждого атома углерода равна
|
n1−1 |
|
j := 0 .. 3 |
q j := ∑ n2 (Cj,i)2 |
qT = ( 1 1 1 1 ) |
i = 0
Для молекулы C4 H6 с четырьмя π - электронами все атомные заряды равны. Рассчитаем теперь индексы свободной валентности. В силу симметрии молекулы крайние атомы углерода и средние должны иметь одинаковые значения. Согласно [17], максимальный порядок π-связи для атома углерода равен Pmax = 1.732. Индекс свободной валентности равен разности Pmax и суммы порядков всех связей, в образовании которых участвует атом. В молекуле бутадиена индекс свободной валентности для крайних и средних атомов соответственно равен:
1.732 − 0.894 = 0.838 ,
78

1.732 − 0.447 − 0.894 = 0.391 .
Рассчитаем теперь матрицу плотности первого порядка.
|
|
|
|
|
|
n1−1 |
|
j := 0 .. 3 |
k := 0 .. 3 |
Pj,k := ∑ n2 Cj,i Ck,i |
|||||
|
|
|
|
|
|
i = 0 |
|
|
|
|
1 |
0.894 |
0 |
−0.447 |
|
|
P = |
0.894 |
1 |
0.447 |
0 |
|
|
|
|
0 |
0.447 |
1 |
0.894 |
|
|
|
|
||||||
|
|
|
|
||||
|
|
−0.447 |
0 |
0.894 |
1 |
|
|
Средняя энергия равна следу произведения матриц H и P. Для вычисления суммы диагональных элементов (следа) произведения матриц воспользуемся встроенной функцией tr() :
Eπ(α,β) = tr(H(α,β) P)
Собираем "конструкцию", копируя содержимое матрицы P через буфер обмена, выделяем все и вызываем операцию (evaluation -> )
|
|
|
|
|
1 |
0.894 |
0 |
−0.447 |
|
|
|
|
( |
α,β |
) |
0.894 |
1 |
0.447 |
0 |
|
→ 4 α + 4.470 |
β |
|
tr H |
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
0.447 |
1 |
0.894 |
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
−0.447 |
0 |
0.894 |
1 |
|
|
|
|
Молекулярные орбитали
Предположим, что атомы углерода в бутадиене расположены вдоль оси X на расстоянии a = 1.4 A, в точках с координатами 0, а, 2а и 3а. Выберем нормированную слэтеровскую орбиталь для 2рz -электрона атома углерода в виде (см., например, [8,16-17]):
Φ(z,x) := 6.145 z exp(−2.599 x ) a := 1.4
Используя найденные собственные векторы составим молекулярные орбитали из атомных орбиталей, центрированных на атомах, по правилу:
3 |
|
Ψ(k ,z,x) := ∑ Cj,k Φ(z,x − j a) |
|
j = 0 |
|
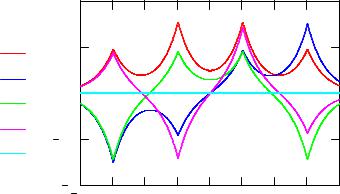
и построим полученные молекулярные орбитали при |
z := 0.2 А |
79
|
1 |
|
|
|
|
|
|
|
|
Ψ(0,z,x) 0.5 |
|
|
|
|
|
|
|
|
|
Ψ(1,z,x) |
|
|
|
|
|
|
|
|
|
Ψ(2,z,x) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ(3,z,x) |
|
|
|
|
|
|
|
|
|
0 |
0.5 |
|
|
|
|
|
|
|
|
|
1 0.7 |
0 |
0.7 |
1.4 |
2.1 |
2.8 |
3.5 |
4.2 |
4.9 |
|
|
|
|
|
x |
|
|
|
|
|
Рис. 3. Молекулярные орбитали в бутадиене при |
||||||||
|
использовании слэтеровских атомных орбиталей |
||||||||
В основном состоянии бутадиена 4 π-электрона занимают две нижние молекулярные орбитали. Поэтому электронная плотность в основном состоянии определяется соотношением:
ρ(z,x) := 2 (Ψ(0 ,z,x)2 + Ψ(1 ,z,x)2)
Эта функция имеет отчетливые пики вблизи ядер и заметные значения между атомами, что не позволяет ясно различать границы между областями, занятыми индивидуальными атомами.
Упрощение векового уравнения
Рассмотрим операции симметрии группы С2 для молекулы бутадиена.
Это тождественное преобразование Е и С2 -поворот на 1800 вокруг оси, проходящей через середину связи атомов 2 и 3. Легко проверить, что матрицы этого приводимого представления имеют вид:
|
1 0 |
0 |
0 |
|
|
0 0 |
0 |
1 |
|
||||
|
|
0 1 |
0 |
0 |
|
|
|
0 0 |
1 |
0 |
|
||
E := |
|
|
C2 := |
|
|
||||||||
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
||
|
|
|
|
|
|
||||||||
|
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
||||
Результаты преобразований, характеры (χ) и характеры неприводимых представлений (A,B) группы С2 показаны в таблице (см. также [9,14-17]).
80
