
QuantMech_Chem_p3_85
.pdfВариационный расчет основного состояния атома гелия Задача 9
Найти энергию и потенциал ионизации основного состояния двухэлектронного атома (иона) вариационным методом, используя в качестве пробных функций произведение водородоподобных функций с эффективным зврядом β , играющим роль вариационного параметра.
Решение
Гамильтониан и пробная функция
Для атома гелия как системы, состоящей из двух электронов с зарядом -е и массой μ и ядра с зарядом Ze, представим гамильтониан без учета спинов частиц в форме
|
−h2 |
|
h2 |
Z e2 |
|
Z e2 |
|
|
|
e2 |
|||
H = |
2 μ |
r1 − |
|
r2 − |
|
− |
|
+ |
|
|
|
, |
|
2 μ |
r |
r |
|
→ → |
|
||||||||
|
|
|
|
|
1 |
|
2 |
|
|
r |
− r |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
где r1 и r2 - координаты электронов относительно ядра.
Выберем пробную функцию в виде произведения двух зависящих от параметра β нормированных водородоподобных функций 1sсостоя-
ния вида |
|
|
|
|
|
|
|
|
|
β3 |
−β (r1 |
+ r2) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
Ψo(r |
1 |
, r |
2 |
, β) = Ψ |
(r |
, β) Ψ |
(r |
, β) = |
|
|
exp |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1s |
1 |
1s |
2 |
|
π a |
3 |
|
a |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где а - боровский радиус, |
β - экранированный заряд ядра [3,4,6]. |
|||||||||||||||
Каждая из функций |
Ψ1s(ri) является собственной для одночастичного |
|||||||||||||||
гамильтониана Hi , (i = 1,2) и полного гамильтониана H0 при β = Z и отсутствии отталкивательного взаимодействия электронов между собой.
H Ψ |
i |
= |
−h2 |
Ψ |
i |
− |
Z e2 |
Ψ |
i |
= E Ψ |
i |
E = |
−μ e4 Z2 |
i |
|
2 μ |
i |
|
ri |
|
i |
i |
2 h2 |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ho Ψo = Eo Ψo |
|
|
|
Eo = E1 + E2 |
|
|||||
Как известно (см. [1-8]), минимум по параметру β средней энергии в состоянии с пробной функцией дает оценку сверху энергии основного состояния, причем точность этой оценки зависит от качества выбора пробной функции.
⌠ |
|
|
|
E ≤ E = min |
Ψo(r1,r2,β)H Ψo(r1,r2,β)dτ1 dτ2 |
⌡ |
|
51

Оценка функционала
Функционал F(β) можно представить в виде трех слагаемых: среднего значения кинетической энергии двух электронов, среднего значения потенциальной энергии их притяжения к ядру и среднего значения энергии их взаимного отталкивания и Е как неопределенного множителя Лагранжа, учитывающего условие нормировки.
F(β) = μ -1< h Ψ1| h Ψ1> −2 Ze2 < Ψ1 | r1-1 | Ψ1> +e2 <Ψo | r12-1 | Ψo> −E
Задаем волновую функцию каждой частицы и проверяем нормировку.
C(β,a) := |
1 |
|
β 3 |
Ψ(r,β,a) := C(β,a) exp |
−β r |
|
|||||
|
π |
a |
|
a |
|
⌠∞
Ψ(r,β,a)2 4 π r2 dr assume,a > 0 ,β > 0 → 1
⌡0
Средние значения кинетической и потенциальной энергии электронов выражаются следующими соотношениями.
|
h2 |
⌠∞ |
|
|
Ψ(r,β,a) 2 4 π r2 dr |
|
T(β,h ,μ ,a) := |
|
d |
||||
|
||||||
|
μ |
⌡ |
|
dr |
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
⌠∞
U(Z,β,a,e2) := −2 Z e2 Ψ(r,β,a)2 4 π r dr
⌡0
Среднее значение потенциальной энергии взаимного отталкивания электронов определяется интегралом
|
⌠ |
⌠ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
V12 = e2 |
Ψo(r1,r2,β) |
|
→ |
→ |
|
Ψo(r1,r2,β)dτ1 dτ2 |
|||
|
|
|
|
||||||
|
|
|
|
|
|
r1 |
− r2 |
|
|
|
⌡ |
⌡ |
|
|
|
|
|
|
|
Для его вычисления можно воспользоваться разложением обратной величины расстояния между электронами по сферическим функциям (см. [2,5,6]), или перейти к эллиптическим координатам. Выберем ось Z вдоль вектора r1 , тогда θ12 = θ2 и модуль разности векторов r12 = |r1 - r2 | не зависит от φ2.
(r12)2 = (r1)2 + (r2)2 − 2 r1 r2 cos(θ2)
52
Элемент объема представляется в виде
dτ1 dτ2 = 4 π (r1)2 2 π (r2)2 sin(θ2) dr1 dr2 dθ2 ,
или, если ν = cos(θ2) ,
dτ1 dτ2 = −4 π (r1)2 2 π (r2)2 dr1 dr2 dν
Определим эллиптические координаты соотношениями |
||||||
s = r + r |
, |
t = r − r |
, |
u = r |
||
1 |
2 |
1 |
2 |
12 |
||
Исходные координаты {r1 , r2 , ν}преобразуются в эллиптические{s, t, u} по формулам
r1(s,t) := |
1 |
(s + t) |
r2(s,t) := |
1 |
(s − t) |
ν(s,t ,u) := |
s2 + t2 − 2 u2 |
||
2 |
2 |
|
|||||||
|
|
|
|
2 |
− t |
2 |
|||
|
|
|
|
|
|
|
s |
|
|
Вычислим частные производные r1,r2 и ν по s, t, u и соберем якобиан
J(s,t,u) замены переменных dr1dr2 dν = J(s,t,u) ds dt du.
dνds(s,t,u) := d ν(s,t,u) simplify |
→ −4 s |
|
t2 − u2 |
|
|||||||||||||
(s2 − t2)2 |
|||||||||||||||||
|
|
|
ds |
|
|
|
|
|
|||||||||
dνdt(s,t ,u) := d ν(s,t,u) simplify |
→ 4 t |
s2 − u2 |
|
|
|||||||||||||
(s2 − t2)2 |
|||||||||||||||||
|
|
|
dt |
|
|
|
|
||||||||||
|
dνdu(s,t,u) := |
d |
|
ν(s,t,u) → −4 |
u |
|
|
|
|
|
|||||||
|
|
|
|
|
|
du |
|
s2 − t2 |
|||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dνds(s,t,u) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
u |
|||
J(s,t,u) := |
1 |
−1 |
|
|
simplify |
|
→ 2 |
|
|||||||||
s2 − t2 |
|||||||||||||||||
|
|
2 |
2 |
|
|
dνdt(s,t ,u) |
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку |
|
0 |
|
|
dνdu(s,t ,u) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−4 π r1(s,t)2 2 π r2(s,t)2 J(s,t ,u) simplify |
→ −u (s − t) (s + t) π2 , |
|
то элемент объема равен |
dτ1 dτ2 = −π2 (s2 − t2)u ds dt du , |
|
причем, |
−u ≤ t ≤ u , |
0 ≤ u ≤ s < ∞ . |
53

В эллиптических координатах интеграл принимает вид
V12(β,a,e2) := e2 π |
⌠∞ |
⌠s ⌠u |
(s2 − t2)exp −2 β s dt du ds |
|
2 C(β,a)4 |
|
|
||
|
|
|
|
a |
|
⌡0 |
⌡0 |
⌡− u |
|
Используя символьный процессор и учитывая, что |
|
|
e2 |
μ e4 |
|||||||||
|
εo = a = |
|
2 |
||||||||||
находим интегралы |
|
|
|
|
|
|
|
h |
|||||
|
|
|
assume,a > 0 ,β > 0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
T(β,h ,μ ,a) |
substitute,μ = |
|
h |
2 |
→ εo β2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
εo a2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
assume,a > 0 |
,β > 0 |
|
|
|
|
|
||||
|
U Z |
,β,a,e2 |
|
substitute,e2 = εo a |
→ −2 Z εo β |
|
|
||||||
|
V12(β,a,e2) |
|
assume,a > 0 |
,β > 0→ |
5 |
εo β |
|
|
|||||
|
|
|
|
||||||||||
|
|
8 |
|
|
|||||||||
|
|
|
|
substitute,e2 = εo a |
|
|
|
|
|
||||
и получаем окончательное выражение для минимизируемой функции.
F(Z,β,εo ,E) := β2 − 2 Z β + 58 β εo − E
Из условия ее экстремума (обращения в нуль производной) получаем оптимальное значение βo - экранированного электронами заряда ядра
|
|
|
|
d |
|
|
2 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
, |
||||
Given |
|
|
db b |
|
− 2 Z b + |
|
b = 0 |
βo(Z) := |
Find(b) → Z − |
|
||||||||||||||||||||
|
|
8 |
16 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
энергию основного состояния |
E(Z,εo) = <Ψ| H |Ψ > |
и потенциал иони- |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
зации I(Z,εo) для гелиеподобной системы с двумя электронами, как |
|
|||||||||||||||||||||||||||||
разность энергий основных состояний с одним и двумя электронами. |
|
|||||||||||||||||||||||||||||
E(Z,εo) := |
βo(Z)2 − 2 Z βo(Z) + |
5 |
βo(Z) |
εo |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||
E(Z,εo) simplify |
|
→ |
−1 |
(256 Z2 |
− 160 Z + 25)εo |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
256 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( |
|
) |
|
|
|
|
|
|
|
|
5 |
|
2 |
|
|
|
|
( |
|
) |
|
Z2 |
( |
|
|
) |
|
|
||
E |
Z,εo |
|
:= − |
|
Z − |
|
16 |
εo |
|
|
I Z,εo |
|
:= − |
2 |
εo − E |
Z,εo |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
54
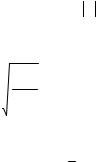
Интересно сопоставить рассчитанные вариационным методом и экспериментальные значения энергий основного состояния и потенциалов ионизации для гелиеподобных систем. Экспериментальные значения энергий (eV) и потенциалов ионизации (V) приведены, например, в [4-5].
Z := 2 .. 6 |
εo := 27.2 eV |
|
E(Z,εo) = |
I(Z,εo) = |
||
"He" |
−78.98 |
24.616 |
|
|
|
|
-77.456 |
|
23.056 |
||||
|
|
|
|
|
|
|
−198.02 |
|
-196.456 |
|
74.056 |
||
"Li+" |
75.616 |
|
|
|||
|
|
|
||||
|
|
-369.856 |
|
152.256 |
||
EIexp := "Be+2" |
−371.5 |
153.775 |
|
|||
"B+3" |
−599.3 |
259.23 |
|
-597.656 |
|
257.656 |
|
|
|
|
-879.856 |
|
390.256 |
"C+4" |
−881.6 |
391.898 |
|
|
|
|
|
|
|
||||
Как показывает анализ этих результатов, точность вариационного расчета значительно улучшается с ростом Z заряда ядра иона, поскольку усиливается связь каждого электрона с ядром.
Упражнения
1.Используя вариационный метод, оценить энергию основного состояния частицы, находящейся в потенциальном силовом поле U(x < 0) = ∞
иU(x > 0) = c x , а в качестве пробной функции выбрать
ψ(x) = A x exp(−β x)
2.Найти вариационным методом энергию первого возбужденного состояния одномерного гармонического осциллятора, используя пробную функцию вида
ψ(x) = A x exp(−β x )
3.Для пробной нормированной волновой функции атома водорода вариационным методом найти минимальное значение энергии.
ψ(r) = |
β3 |
exp |
−β r |
||
|
3 |
a |
|
||
|
π a |
|
|||
|
|
|
|
|
|
4.Вариационным методом, используя пробную функцию вида
ψ(r) = A exp −β r 2
a
найти энергию основного состояния атома водорода, а также среднее <r> и наиболее вероятное значение rвер для этой функции.
55
5. Используя разложение обратного расстояния между частицами по сферическим функциям (см.[2,4-6]) при r1 > r2 и r1 < r2 соответственно, показать, что имеет место соотношение
⌠ |
⌠ |
exp(−α r1 − γ r2) |
|
|
32 π2 (α2 |
+ γ2 + 3 α γ) |
|||||
|
|
|
= |
||||||||
|
|
|
|
dτ1 dτ2 |
|
|
|
|
|
||
|
→ → |
|
|
2 |
2 |
(α + γ) |
3 |
||||
|
|
|
r1 − r2 |
|
|
|
α |
||||
|
|
|
|
|
|
|
γ |
|
|||
⌡ |
⌡ |
|
|
|
|
|
|
|
|
|
|
и вычислить среднюю энергию взаимодействия электронов между собой в состоянии с использованной выше пробной функцией Ψo(r1,r2,β).
6. Выполняя интегрирование по частям, показать, что
⌠ |
exp(−α r) |
((exp(−γ r)) dτ = |
−8 π α γ |
|
|||
⌡ |
|
|
(α + γ)3 |
7. Найти среднюю энергию основного состояния иона Н- , выбирая пробную функцию в виде [4,c. 120]
Ψ(r1,r2) = C (exp(−a r1 − b r2)+ exp(−b r1 − a r2))
Определить оптимальные значения параметров a и b и сравнить полученное и экспериментальное значение −0.5278εo = −14.356 eV энергий. Устойчиво ли это состояние иона относительно автоионизации?
8. Выбирая пробную волновую функцию с учетом корреляции электронов на близких расстояниях в виде (a и β - вариационные параметры)
Ψ(r1,r2) = C exp −β (r1 + r2) (1 + a r12) ,
и вычисляя интегралы в эллиптической системе координат (см. выше) получить в атомной системе единиц (h=μ=e=εo=1) выражения для сред-
них значений кинетической и потенциальной энергий двух электронов |
|||||||||||||||||||||||||||
− 1 |
= |
|
2 |
+ |
8 |
β2 + |
β |
U = |
− β |
( |
4 |
β2 |
+ |
15 |
β |
a |
+ |
2) |
|||||||||
A |
|
48 a |
|
|
|
|
|
35 a |
|
β2) |
4 |
|
Z A |
|
|
|
|
|
18 a |
|
|||||||
T = |
β2 |
( |
32 |
|
a |
2 |
+ |
β + |
8 |
V12 = |
β ( |
|
|
|
2 |
+ |
32 |
β |
a |
+ β2) |
|||||||
|
|
A |
|
|
|
25 a |
|
|
|
A |
35 a |
|
|
|
10 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
9. Используя результаты упражнения 8, найти оптимальные значения параметров a и β, вычислить энергии основных состояний гелиеподобных ионов (H--, He, Li+ и т.д.) и сравнить с однопараметрическими расчетами.
56

Стационарная теория возмущений Задача 10
В рамках стационарной теории возмущений найти: а) поправку первого и второго порядка к энергии основного состояния гармонического осциллятора с потенциалом возмущения V(x)= a|x| ; б) поправку первого порядка к энергии основного и первого возбужденного состояний атома водорода, находящегося в однородном электрическом
поле с напряженностью ε.
Решение
Ангармонический осциллятор
Рассмотрим задачу о стационарных состояниях для ангармонического осциллятора с гамильтонианом вида
−h2 |
d2 |
k x2 |
|
|
, |
||||||
H = 2 μ |
|
+ |
2 |
+ a |
x |
||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
||||
|
dx |
|
|
|
|
|
|
|
|
||
где возмущение задается потенциалом |
|
V(a,x) := a |
|
x |
|
|
|||||
|
|
||||||||||
Невозмущенная задача при V(a,x) = 0 имеет дискретный невырожденный |
|||||||||||
спектр. Определим энергии и волновые функции нескольких первых состояний невозмущенной задачи следующим образом [1-3]:
E0(n ,hω) := hω n + |
1 |
|
|
|
|
|
|
b = |
h |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
μ ω |
|||||
|
|
|
|
1 |
|
−1 x |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
Ψ0(x ,b) := |
b π exp 2 |
|
|
|
|
|
|
|
|||||||||
H(n ,x) := (−1)n exp(x2) |
dn |
|
(exp(−x2)) |
|
|
|
|
||||||||||
dx |
n |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
1 |
|
|
−1 |
|
x |
x |
||||||||
|
|
|
|
|
|
|
|
|
b |
|
H n , b |
||||||
Ψ(n ,x ,b) := |
2 |
n |
n! |
|
|
exp 2 |
|
||||||||||
|
|
π b |
|
|
|
|
|
|
|
|
|
|
|||||
Поправка первого порядка к энергии в основном состоянии |
< 0 | V | 0 > |
||||||||||||||||
равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⌠∞ |
Ψ0(x ,b)2 V(a,x) dx assume,b > 0 |
|
b |
|
|||||||||||||
E1(a,b) := |
→ |
a |
|||||||||||||||
|
|||||||||||||||||
⌡ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 2
Для вычисления поправок второго порядка потребуются матричные элементы < m | V | 0 > от потенциала возмущения V(a,x) вида [1-3]
57

⌠∞
U(m,a,b) := Ψ(m,x ,b) V(a,x) Ψ0(x ,b) dx
⌡− ∞
При вычислении будем учитывать вклады только первых четырех возбужденных состояний (m =1..4 иm ≠ n = 0) гармонического осциллято-
ра.
4 |
U(m,a,b)2 |
E2(a,b ,hω) = ∑ |
|
(E0(0 ,hω) − E0(m,hω)) |
|
m = 1 |
|
Принимая во внимание свойства четности состояний осциллятора, можно ожидать, что поправки второго порядка от нечетных состояний осциллятора к энергии основного состояния будут равны нулю, а ненулевые вклады отрицательны и быстро убывают с ростом m - номера состояния.
U(1 ,a,b) assume,b > 0 → 0 |
|
U(3 ,a,b) assume,b |
> 0 → 0 |
|||||||
|
U(2 ,a,b)2 |
|
assume,b > 0 |
−1 |
|
b2 |
a2 |
|||
|
|
|
||||||||
|
|
|
simplify |
→ |
|
|
|
|
|
|
|
(E0(0 ,hω) − E0(2 ,hω)) |
|
4 |
π |
hω |
|||||
|
|
|
|
|||||||
|
U(4 ,a,b)2 |
|
assume,b > 0 |
−1 |
|
b2 |
a2 |
|||
|
|
|
||||||||
|
|
|
simplify |
→ |
|
|
|
|
|
|
|
(E0(0 ,hω) − E0(4 ,hω)) |
|
96 |
π |
hω |
|||||
|
|
|
|
|||||||
Суммарный вклад второго порядка от всех учитываемых состояний
равен
E2 = −25 b2 a2 96 π hω
Таким образом, энергия основного состояния с учетом поправок равна
E = |
1 |
hω + |
a b |
− |
25 |
|
b2 |
|
a2 |
b = |
h |
|
2 |
π |
96 |
π |
hω |
μ ω |
|||||||
|
|
|
|
|
|
Условием применимости является требование малости коэффициентов разложения волновой функции первого приближения по базису невозмущенной задачи (см. [1-6]).
U(m,a,b)
C(m) = (E0(0 ,hω) − E0(m,hω))
Поскольку вклады нечетных состояний равны нулю, а наибольший вклад вносит второе состояние, то это требование выражается неравенством
58
|
|
U(2 ,a,b) |
|
a b |
|
2 |
|
a |
2 |
|
|
||
|
E0(0 ,hω) − E0(2 ,hω) |
= 4 h ω |
|
π |
= |
4 ω |
π h ω μ |
< 1 |
|||||
Вычисляя коэффициенты для второго и четвертого состояний, находим |
|||||||||||||
первое приближение для волновой функции основного состояния |
|||||||||||||
Ψ1(x ,a,b ,hω) = −a b |
2 Ψ(2 ,x ,b) + a b |
6 Ψ(4 ,x ,b) |
|||||||||||
|
|
|
|
4 hω π |
|
|
|
48 hω |
π |
|
|
||
Пусть параметры потенциала соответствуют частоте колебаний моле- |
|||||||||||||
кулы водорода, а масса частицы - приведенная масса двух атомов водо- |
|||||||||||||
рода (см. задачу 3 данного пособия). Если принять следующие значения |
|||||||||||||
для констант |
|
|
|
|
|
|
|
|
|
|
|
||
k := 32.0 |
eV A− 2 |
μc2 := 0.5 938.28 106 eV |
hc := 1.9732858 103, |
||||||||||
то частота колебаний и параметр b равны: |
|
|
|
|
|
|
|||||||
ω := |
k μc2− 1 |
b := |
hc |
b = 0.127 |
A |
|
Пусть |
a := 1.5 eV A− 1 |
|||||
|
|
|
|
μc2 ω |
|
|
a b |
|
2 = 0.074 |
|
|
||
Проверим критерий применимости |
|
|
|
|
|||||||||
|
|
|
|
|
|
4 hc ω π |
|
b2 |
a2 |
||||
Поправки |
Eo := hc ω |
E1 := |
a b |
|
E2 := −25 |
||||||||
|
|
|
|
2 |
|
|
|
π |
|
|
96 |
π |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
hc |
|
Eo = 0.258 |
eV |
|
E1 = 0.107 |
eV |
|
|
|
E2 = −5.828 × 10− 3 eV |
|||||
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
0.5 k x2 |
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
V(a,x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Eo |
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
Eo+E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Eo+E1+E2 0.1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 0.4 |
0.2 |
|
0 |
|
|
|
0.2 |
|
0.4 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
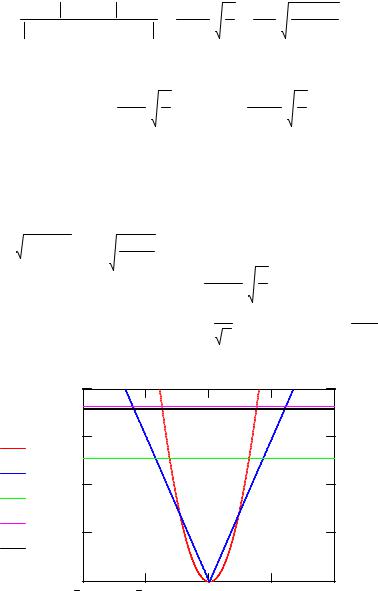
Рис. 1. |
Потенциалы и энергия основного состояния с учетом поправок |
||||||||||||
59
Оценим поправки к волновой функции основного состояния от второго и четвертого состояний в первом порядке теории возмущений. При вы-
бранном значении параметра a = 1.5 eV A-1 они составляют менее 7%.
Ψ12(x) :=
Ψ01(x)
Ψ0(x,b)
Ψ12(x)
Ψ14(x)
−a b |
|
2 |
Ψ(2 ,x ,b) |
Ψ14(x) := |
a b |
|
6 |
Ψ(4 ,x ,b) |
4 hc ω |
π |
|
π |
|||||
|
|
48 hc ω |
|
|
||||
Ψ01(x) := Ψ0(x ,b) + Ψ12(x) + Ψ14(x)
2
1
0
0.4 |
|
0.2 |
0 |
0.2 |
0.4 |
|
x
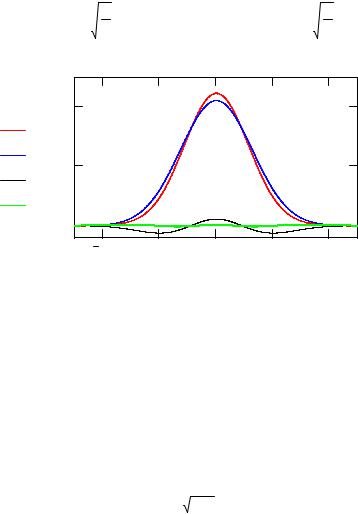
Рис. 2. Волновая функция основного состояния и вклады первого порядка от состояний с m = 2 и m = 4
Атом водорода в электрическом поле
Пусть напряженность однородного электрического поля ε направлена вдоль оси Z. Тогда потенциал возмущения может быть представлен как скалярное произведение дипольного момента и напряженности поля (q - заряд электрона). V(qε,r,θ) := −qε r cos(θ)
Основное состояние атома водорода невырождено. Волновая функция имеет вид
|
1 |
−r |
, |
Ψ0(r,r1) := |
|
exp r1 |
|
r1 π r1 |
а поправка первого порядка для этого состояния равна нулю.
⌠∞ ⌠π
V(q ,r,θ) Ψ0(r,r1)2 2 π r2 sin(θ)dθ dr assume,r1 > 0 → 0
⌡0 ⌡0
60
