
01
.pdf
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Задача 48
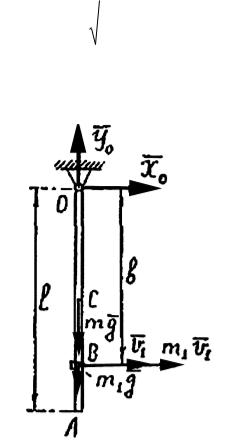
Тонкий однородный стержень массы m и длиной OA l может вращаться без трения вокруг горизонтальной оси О . В начальный момент времени стержень отведен в горизонтальное положение и отпущен без начальной скорости. Определить угловую скорость и угловое ускорение стержня, когда он повернется на угол .
Решение.
По теореме об изменении кинетического момента системы составим дифференциальное уравнение вращательного движения стержня вокруг оси О.
J ddt mg 2l cos .
Учитывая, что момент инерции стержня равен:
|
J |
ml2 |
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
||
|
d |
|
3g cos |
|
|
|
|||||||
dt |
|
|
2l |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
Воспользуемся подстановкой, |
d |
|
|
d |
|
d |
|
d |
|||||
|
|
d dt |
d |
||||||||||
|
|
|
dt |
|
|
|
|||||||
d 3g cos . d 2l
Разделим переменные и проинтегрируем исходное дифференциальное уравнение вращательного движения стержня с учетом начальных условий движения (при =0, 0 =0
d 3g cos d 2l
141
2 |
3g sin |
|
|
|
||
|
|
|
|
. |
|
|
|
|
|
||||
2 |
|
|
2l |
|
|
|
Угловая скорость стержня |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3g sin |
. |
||
|
|
|
||||
|
|
|
l |
|
|
|
Задача 49 (рис. 69)
Рисунок 69
Доска ОА массой m =4кг и длиной l =1м может вращаться без трения вокруг горизонтальной оси О. В неподвижную доску на расстоянии b =0.8м
от оси О попадает и застревает пуля массой m1 =0.01кг, летевшая со скоростью V1 =800м/с. Определить угловую скорость доски после попадания пули. При вычислении момента инерции доску считать однородным стержнем.
Решение. (рис. 70)
142
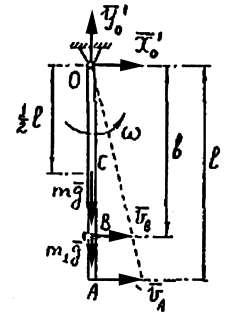
Рисунок 70
На доску действуют силы: mg , а также составляющие реакций оси Х О
и YО (рис. 69). После попадания пули в доску действуют силы: mg , m1g , а
также составляющие реакций оси ÕÎ и YÎ (рис. 70).
На основании теоремы об изменении кинетического момента имеем
dK z m F e ; m F e 0; K const K .
dt z k z k z z 0
Это уравнение называется законом сохранения кинетического момента системы относительно оси.
Тогда следует K z 0 m1V1b , (доска неподвижна)
K z m1V1b J z (m1b2 |
|
ml2 |
) , где |
J z |
ml2 |
-момент инерции доски |
||||||
|
|
|
|
|||||||||
|
|
|
3 |
|
|
3 |
|
|
||||
относительно оси Oz, V b . |
|
|
|
|
|
|
|
|
|
|
|
|
С помощью равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
m V b |
ml2 |
m b2 , |
|
|
|||||||
|
|
|
||||||||||
1 |
1 |
3 |
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
Определим угловую скорость доски |
|
|
|
|
||||||||
|
3m1V1b |
|
|
|
3 0.01 800 0.8 |
|
4.8 рад/с. |
|||||
ml2 3m b2 |
4 12 3 0.01 0.82 |
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
143 |
Задача 50 (рис. 71)
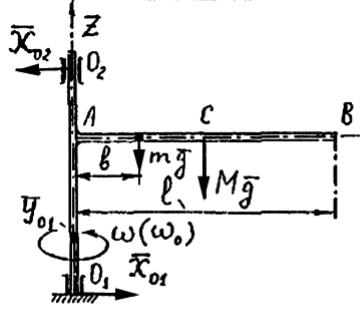
Горизонтальная трубка длиной l может свободно вращаться вокруг вертикальной оси О1О2 . Внутри трубки на расстоянии b от оси находится шарик массой m . В начальный момент трубке сообщается начальная угловая скорость 0 . Момент инерции трубки относительно оси вращения J z .
Пренебрегая потерями на трение, определить угловую скорость трубки в момент, когда шарик вылетит из трубки.
Рисунок 71
Решение. (рис. 71)
На систему тел действуют внешние силы: Мg , mg , а также составляющие реакций опор оси ХО1 , YО1 , Х О2 .
На основании теоремы об изменении кинетического момента имеем
dK z m F e ; m F e 0; K const K .
dt z k z k z z 0
В данном случае выполняется закон сохранения кинетического момента системы относительно оси. Составим уравнение
Kz 0 mvb J z 0 (mb2 J z) 0 , Kz mvl J z (ml2 J z) ,
144
где v0 и v -скорость шарика соответственно в начальном и конечном положении во вращательном движении вместе с трубкой вокруг оси O1O2
(оси O1z ) v0 = 0 b, v= l .
Угловая скорость трубки
J |
m l 2 J |
|
0 |
m |
b2 . |
||
z |
|
|
z |
|
0 |
|
|
|
J mb2 |
|
|
|
|
||
J ml2 0 ;( 0). |
|||||||
|
|
z |
|
|
|
|
|
z
Задача 51 (рис. 72)
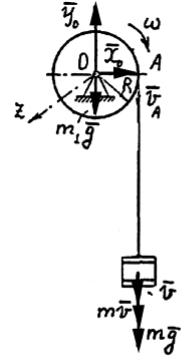
Груз массой m подвешен на тросе, навитом на барабан массой m 1 с
горизонтальной осью вращения. Пренебрегая потерями на трение и считая барабан сплошным однородным цилиндром, определить ускорение груза.
Рисунок 72
Решение. (рис. 72)
На систему тел действуют внешние силы: m1g , mg , а также составляющие реакций опор оси Х О , YО .
На основании теоремы об изменении кинетического момента имеем
145

dK z mz F e ; mz F e mgR. dt k k
Кинетический момент системы относительно оси вращения барабана:
K z
где VR , J z 12 m1 R2
Далее получим
|
mVR |
m1 |
|
|
z |
|
|
|
|
J |
|
|
m VR , |
|
|
|
2 |
|
|
(V скорость груза; R радиус барабана).
m1 |
|
dV |
|
dV |
|
|
|
|
m R |
|
mgR;a |
|
.. |
|
|
|
||||
|
2 |
|
dt |
|
dt |
|
Ускорение груза
2mg
a m 2m .
1
Задача 52 (рис. 73)
Через блок массой m1 0.2m , имеющего горизонтальную ось вращения,
переброшена веревка, к одному концу которой подвешен груз массой m , а за другой конец ухватился человек, имеющий ту же массу m . Пренебрегая массой веревки и считая массу блока равномерно распределенной по его ободу, определить скорость груза, если человек начнет подниматься по веревке с относительной скоростью u .
146

Рисунок 73
Решение. (рис. 73)
На систему тел действуют внешние силы: mg , m1g , а также составляющие реакций опор оси Х О , YО .
На основании теоремы об изменении кинетического момента имеем
dK z m F e ; m F e mgr mgr 0
dt z k z k
K z const K z 0 ; K z 0 0; K z 0.(по условию задачи)
В данном случае выполняется закон сохранения кинетического момента системы относительно оси. Составим уравнение
mvr J z m(u v)r 0;
где Jz=1/2 (m1 r2) =0,1 (m r2).Здесь m1 =0,2m = v/r-угловая скорость блока .
m(u v)r 0.1mr 2 vr mvr 0 .
Скорость груза
147
v 1021u .
Задача 53 (рис. 74)
Через блок массой M , имеющий горизонтальную ось вращения,
переброшен трос, к одному концу которой подвешен груз массой m , а
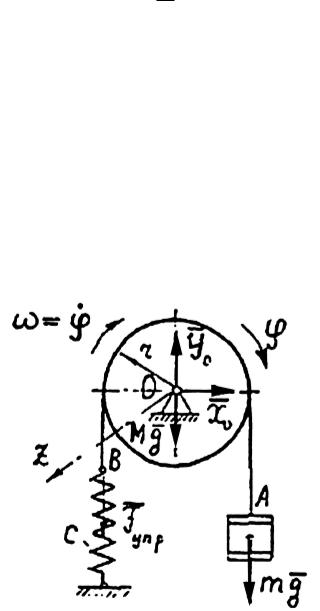
другой конец прикреплен к пружине жесткостью с . Пренебрегая трением и массой троса определить период малых колебаний системы, считая блок однородным цилиндром.
Рисунок 74
Решение. (рис. 74)
На рассматриваемую систему тел действуют внешние силы: Mg , mg ,
сила упругости пружины Fпр , а также составляющие реакций опор оси Х О ,
YО .
Дифференциальное уравнение малых свободных колебаний диска получим с помощью теоремы об изменении кинетического момента:
148

dK z |
mz F ek . |
|
|
dt |
F ek mgr F óïð |
|
|
mz |
f mgr c( f ct f )r c r2 , |
||
где F óïð c( f ct |
f ) -упругая сила пружины; f r - деформация |
||
пружины, здесь -угол поворота блока (малый угол). |
|||
В положении статического равновесия |
|
||
|
F óïð r mgr |
или c f cò mg. |
|
Кинетический момент системы относительно оси вращения барабана: |
|||
|
K z J z |
mVr J ïðz . |
. |
|
|
|
|
где J z 12 m r2 -момент инерции блока относительно оси вращения;
ïð |
M |
|
2 |
|
|
V r - скорость груза, -угловая скорость блока; J z |
|
|
m r |
|
- |
|
|
||||
|
|
2 |
|
|
|
приведенный момент инерции системы.
Таким образом, проектируя уравнение на ось вращения блока, получим
учитывая, что |
d |
) |
|
|
|
|
dt |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
J ïðz cr 2 0; |
k 2 |
|
d |
. |
|
|
|
||||
|
|
|
|
|
dt |
|
Круговая частота колебаний будет равна:
|
c r2 |
|
2ñ |
|
|
|
k |
|
|
|
. |
||
|
|
|||||
|
J ïðz |
M 2m |
|
|
||
Период малых колебаний системы
T |
2 |
2 |
|
M 2m |
|
. |
|
|
|||||
|
k |
|
|
2c |
||
Задача 54 (рис. 75)
149
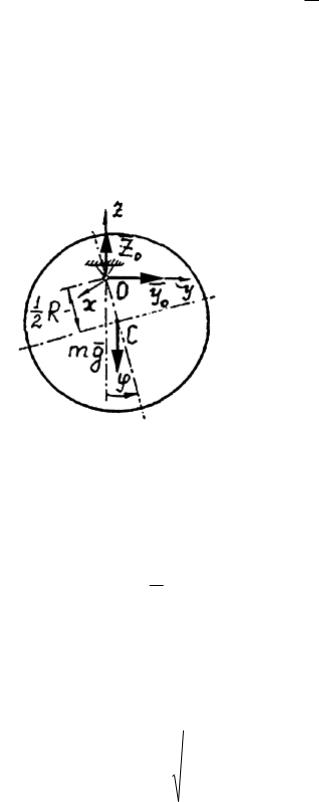
Вертикально расположенный диск имеет горизонтальную ось вращения,
смещенную относительно центра масс диска на расстояние ОС R2 . В
начальный момент угол отклонения диска от равновесного положения равен0 , а начальная скорость равна нулю. Считая колебания диска малыми определить закон движения диска.
Решение. (рис. 75)
Рисунок 75
Диск является физическим маятником. Дифференциальное уравнение вращательного движения диска имеет вид:
J mz F ek .
mz F ek mg R2 sin ,
где sin ; -угол поворота блока (малый угол).
mg |
R |
sin |
mgR |
. |
|||||||
|
|
|
|
||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mg |
R |
|
|
|
|
|
|
|
|
|
|
|
|||||
k 2 0 где |
k |
2 |
. |
||||||||
|
|||||||||||
|
|
|
|
|
|
J z |
|||||
Момент инерции диска относительно оси вращения:
150
