Линейное программирование. Геометрическое решение задач линейного программирования.
В общей постановке задача линейного программирования состоит в отыскании значений n-переменных x1, x2…xn доставляющих экстремум функции W=∑ci*xi при условиях:
A11*x1+a12*x2+…+a1n*xn ≤ b1
A21*x1+a22*x2+…+a2n*xn ≤ b2
………………………………
Am1*x1+am2*x2+…+amn*xn ≤ bm Для всех xi≥0
Оптимальное решение задачи линейного программирования ищут среди дополнительных базисных решений.
Геометрический подход к решению задач линейного программирования
Используется для наглядной иллюстрации смысла существования подобных задач.
Предприятие выпускает три вида тары в количествах:
В1= 700 ед, В2= 800ед. В3= 600ед.
Отправка одной партии каждого набора требует следующего расхода тары:
|
Вид тары |
1 |
2 | |
|
I |
3 |
5 | |
|
II |
8 |
1 | |
|
III |
4 |
7 | |
Рыночный спрос на одну партию набора 1-го вида обеспечивает доход в 8 ден. ед., а второго в 6 ден. ед.. Требуется определить объемы реализации на рынке партии товаров из наборов каждого вида, обеспечивающие максимум прибыли его производителям.
Геометрическое решение задачи:
1)Постановка задачи
Найти x1,x2, доставляющие максимум целевой функции w=8+1+6x2
При ограничениях :3*x1+5*x2≤700
8*x1+1*x2≤800
4*x1+1*x2≤600
x1≥0,x2≥0
От линейных неравенств перейдем к уравнениям:
3*x1+5*x2=700 x1=0 x2=145 x2=0 x1=233
8*x1+1*x2=800 x1=0 x2=100 x2=0 x1=100
4*x1+7*x2≤600 x1=0 x2=85 x2=0 x1=150
X2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1
0 100 200 300 400 500 600
W1= 8*0+6*85 =510
W2= 8*50+6*75 = 850
W3 = 8*100+ 6*0 = 800
W4= 8*0 + 6*0 = 0
Вывод: Найденные значения являются объемами реализации на рынке партии товаров из наборов каждого вида, обеспечивающие максимум прибыли его производителям.
Оптимизационные модели фрагментов логистической инфраструктуры.
Задача. Контактный провод для электропоездов подвесили на столбах расположенных на расстоянии 20м друг от друга.
Наибольшая допустимая величина провисания провода 20см на расстоянии 2 м от столба провод провисает на величину y=5,5 см. Уравнение прогиба провода: y=ax^2+bx +c
Требуется установить максимальный прогиб между опорами x=10м
Решение. С учетом того что прогиб провода в точках подвеса равен нулю можно записать:
1 Точка 0=a*0^2+b*0+c отсюда следует с=0
2 Точка 0=a*20^2+b*20+c
На расстоянии 2 метров от первого столба прогиб равен: -0,055=a*2^2+b*2+с
Составим систему уравнений:
0=а*20^2+b*20
-0,055=a*2^2+b*2
b=-20a
-0,055=-36a
b=-20
a=-0,055/-36
b=-0,0305
a=0,0015
Полученные значения подставляем в уравнение: y=a*10^2+b*10:
y=0,0015*100+(-0,0305)*10
y=-0,155
Прогиб 15,5 см
Вывод: величина прогиба провода не превышает нормы.
Между А и В 46 км. Через В на расст. 35 км автомагистраль. До автомаг. от А предполаг. постр.подъез. дорогу. Под каким α к автомаг. необх. проложить подъездной путь чтобы движение из А в В заняло мин. время?
V по магистрали = 90 км/ч
V по подъездной дороге = 45 км/ч
Решение
АВ=46 км АD=35км. Требуется найти уг. α
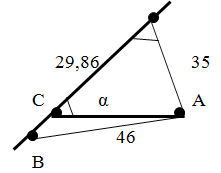
Решение:
T=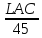
+
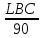
LBD=
=29,84
LCD=
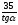
LBC
= LBD
–
LCD
= 29,84
-
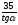. Подъездная
дорога: Sin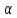
=
;
LAC
=
=
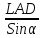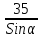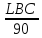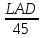;T
=
+
;
T
=
+
|
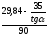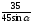
α |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
Значение |
2,605 |
1,537 |
1,213 |
1,078 |
1,020 |
1,005 |
1,017 |
1,052 |
T
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
α
Ответ:
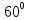обеспечивает минимум функцииT(α)