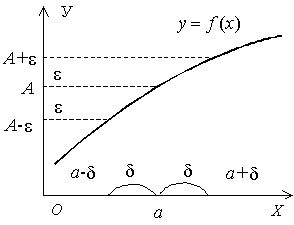15.Функции. Последовательность как функция дискретного аргумента.

16. Бескоечно большие, бесконечно малые и ограниченные велечины и их свойства.

Бесконечно малые и бесконечно большие величины

Бесконечно малая величина есть такая переменная величина, предел которой есть 0, или, что то же самое, это есть такая переменная величина, которая может быть сделана менее всякой данной величины. Поэтому Б. м. величину называют также иногда произвольно малою величиной. Б. большая величина, или произвольно большая величина, напротив, есть такая, которая может быть сделана более всякой данной величины. Эти два вида переменных величин взаимно соответствуют один другому и должны быть рассматриваемы вместе. Так, в элементарной геометрии разность между длиной окружности круга и периметром вписанного или описанного многоугольника с произвольно большим числом сторон есть величина произвольно малая. Б. малые и Б. большие величины делят на различные порядки. Выбирая из данных переменных величин одну какую-нибудь за малую величину первого порядка, называют Б. малыми величинами того же первого порядка всякую Б. малую величину, отношение которой к данной есть величина конечная. Если же отношение это есть Б. малая величина и притом 1-го порядка, то ее называют Б. малой величиной 2-го порядка и т. д. Таким образом, если, напр., α есть бесконечно малая величина, а k какая-нибудь конечная величина, то kα есть также Б. малая величина 1-го порядка, а αⁿ есть Б. малая величина n-го порядка. В то же время 1/α считается Б. большой величиной 1-го порядка, 1/αⁿ — Б. большой величиной n-го порядка и т. д. Порядок малости или великости какой-нибудь переменной величины может быть не только целый, но и дробный, или иррациональный; так, напр., при Б. большом х 1-го порядка величина logx есть Б. большая величина Б. малого порядка. Громадное значение, какое имеют Б. малые величины в анализе, основано на следующих двух положениях: I. При разыскании предела отношения двух выражений, содержащих Б. малые величины различных порядков, можно отбросить все Б. малые величины кроме тех, порядок которых наименьший. II. При разыскании предела суммы выражения, содержащего Б. малые величины различных порядков, можно отбросить все Б. малые величины кроме тех, порядок которых наименьший. На этих положениях основано все дифференциальное и интегральное исчисление (см, это сл.). В течение долгого времени эти свойства Б. малых величин казались парадоксальными и возбуждали споры и возражения со стороны многих математиков.

Предел функции

Пусть дана функция y = f (x), определенная на множестве значений аргумента, содержащего некоторую точку а. Рассмотрим -окрестность точкиа, где - малое положительное число:

.

Пусть для значений x, достаточно близких к а, т. е. принадлежащих d -окрестности точки а, соответствующие значения функции y=f(x) неограниченно приближаются к некоторому числу А. Это значит, что разность ( f (x) - A) все время уменьшается. В этом случае число А называется пределом функции y = f (x) при .

О п р е д е л е н и е 1. Число А называется пределом функции y = f (x) при , если для любого сколь угодно малого e найдется малое положительное, такое, что для всех значений х, удовлетворяющих неравенствубудет выполняться неравенство (рис. 63):

.                                                  (4.2)

Неравенство означает, что значения функцииy = f (x) попадают в e -окрестность точки А на оси ОУ.

Из рис. 63 следует, что, если число А есть предел функции y= f (x) при , то как только значения независимой переменнойх попадут в -окрестность точкиа, так сразу соответствующие значения функции попадут в -окрестность точкиА, т. е. график функции будет целиком лежать в полосе шириной 2e .	Рис. 63
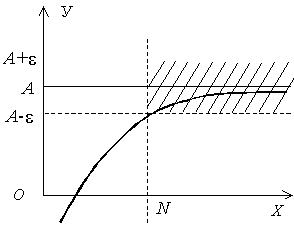
О п р е д е л е н и е 2. Число А называется пределом функции y = f (x) при , если для всякого положительного сколь угодно малого e найдется такое положительное число, что для всех значений х, удовлетворяющих условию, будет выполняться неравенство (рис. 64). (4.3)	Рис. 64