25. Дефференциал.

Пусть функция дифференцируема в точке , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно и нелинейного членов:

где при .

Определение

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как или . Таким образом:

Замечание

Дифференциал функции составляет основную часть ее приращения.

Замечание

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Замечание

Формулу для дифференциала функции можно записать в виде:

Отсюда получаем, что

Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.

Геометрический смысл дифференциала

Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .

Пусть функция y = f(x) дифференцируема при некотором значении переменной x . Следовательно, в точке x существует конечная производная

Тогда по определению предела функции разность

                            (1)

является бесконечно малой величиной при . Выразив из равенства (1) приращение функции, получим

                    (2)

(величина  не зависит от , т. е. остаётся постоянной при ).

Если , то в правой части равенства (2) первое слагаемое линейно относительно . Поэтому при

оно является бесконечно малой того же порядка малости, что и . Второе слагаемое - бесконечно малая более высокого порядка малости, чем первое, так как их отношение  стремится к нулю при

Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

                (3)

Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают

или

Следовательно,

                   (4)

или

             (5)

Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Дифференциал обладает свойствами, аналогичными свойствам производной:

 (С – постоянная величина)  (8)

                                (9) (10)

                                      (11)

                            (12)

Формулы (8) – (12) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Рассмотрим дифференциал сложной функции. Пусть - сложная функция :

Дифференциал

этой функции, используя формулу для производной сложной функции, можно записать в виде

Но  есть дифференциал функции , поэтому

,

т.е.

                                      (13)

26. Теорема лагранжа о конечном приращении.

Следующее утверждение является одним из наиболее часто используемых и важных средств исследования числовых функций.

Теорема 1 (теорема Лагранжа о конечном приращении). Если функция  непрерывна на отрезке  и дифференцируема в интервале  то найдется точка  такая, что

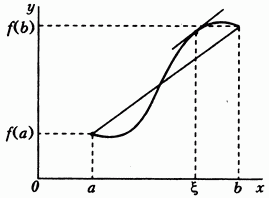
Рис. 21

Для доказательства рассмотрим вспомогательную функцию

которая, очевидно, непрерывна на отрезке  дифференцируема в интервале  и на его концах принимает равные значения:  Применяя к теорему Ролля, найдем точку  в которой

Замечания к теореме Лагранжа. 1° Геометрически теорема Лагранжа означает (рис. 21), что в некоторой точке  где 

касательная к графику функции будет параллельна хорде, соединяющей точки  ибо угловой коэффициент последней равен 

2° Если х интерпретировать как время, а  — как величину перемещения за время  частицы, движущейся вдоль прямой, то теорема Лагранжа означает, что скорость  частицы в некоторый момент  такова, что если бы в течение всего промежутка времени  частица двигалась с постоянной скоростью  то она сместилась бы на ту же величину  Величину  естественно считать средней скоростью движения в промежутке 

3° Отметим, однако, что при движении не по прямой средней скорости в смысле замечания 2° может не быть. Действительно, пусть, например, частица движется по окружности единичного радиуса с постоянной угловой скоростью Закон ее движения, как мы знаем, можно записать в виде

Тогда

В моменты  частица находится в одной и той же точке плоскости  и равенство

означало бы, что  но это невозможно.

Однако мы сознаем, что зависимость между перемещением за некоторый промежуток времени и скоростью движения все же имеется. Она состоит в том, что даже вся длина  пройденного пути не может превышать максимальной по величине скорости, умноженной на время в пути. Сказанное можно записать в следующей более точной форме:

Как будет в свое время показано, это естественное неравенство действительно всегда справедливо. Его тоже называют теоремой Лагранжа о конечном приращении, а формулу (2), справедливую только для числовых функций, часто называют теоремой Лагранжа о среднем значении (роль среднего в данном случае играет как величина  скорости, так и точка  лежащая между а и 

4° Теорема Лагранжа важна тем, что она связывает приращение функции на конечном отрезке с производной функции на этом отрезке. До сих пор мы не имели такой теоремы о конечном приращении и характеризовали только локальное (бесконечно малое) приращение функции через производную или дифференциал в фиксированной точке.

Следствия теоремы Лагранжа

Следствие 1 (признак монотонности функции). Если в любой точке некоторого интервала производная функции неотрицательна (положительна), то функция не убывает (возрастает) на этом интервале.

Действительно, если  — две точки нашего интервала и  то по формуле (2)

и, таким образом, знак разности, стоящей в левой части равенства, совпадает со знаком 

Разумеется, аналогичное утверждение можно высказать о невозрастании (убывании) функции с неположительной (отрицательной) производной.

Замечание. На основании теоремы об обратной функции и следствия 1, в частности, можно заключить, что если на каком-то промежутке I числовая функция  имеет положительную или отрицательную производную, то функция  непрерывна на  монотонна на  имеет обратную функцию  определенную на промежутке  и дифференцируемую на нем.

Следствие 2 (критерий постоянства функции). Непрерывная на отрезке  функция постоянна на нем тогда и только тогда, когда ее производная равна нулю в любой точке отрезка  (или хотя бы интервала 

Интерес представляет только доказательство того факта, что если  на  то для любых  имеет место равенство  Но это вытекает из теоремы Лагранжа, по которой

ибо  лежит между 

Замечание. Отсюда, очевидно, можно сделать следующий (как мы увидим, очень важный для интегрального исчисления) вывод: если производные двух функций  совпадают на некотором промежутке, т. е.  то на этом промежутке разность  есть постоянная функция.

Полезным обобщением теоремы Лагранжа, которое тоже основано на теореме Ролля, является следующее

Утверждение 2 (теорема Коши о конечном приращении). Пусть  — функции, непрерывные на отрезке  и дифференцируемые в интервале 

Тогда найдется точка  такая, что