Математика. Комплексный анализ, часть 2

4ГЛАВА 4. НЕКОТОРЫЕ КЛАССЫ ГОЛОМОРФНЫХ ФУНКЦИЙ

является обратной к ней.

З а д а ч а 4.1.1. Найти функцию, обратную к

f(z) = 2z + 3:

Р е ш е н и е. z = w2 3 :

З а д а ч а 4.1.2. Во что переводит функция z1 прямую y = 3x?

Р е ш е н и е. Так как все точки луча y = 3x; x > 0 имеют один и тот же аргумент, его образом будет луч y = 3x; x > 0. Аналогично, образом луча y = 3x; x < 0 является луч y = 3x; x < 0. Точка 1 переходит в 0, а 0 переходит в 1.

Свойства дробно-линейных функций

через 1 (то есть 1(t1) = 2(t2) = 1 для некоторых t1 2 ( 1; 1); t2 2 ( 2; 2)), такие, что их сферические образы при стереографической проекции имеют касательные в северном полюсе. Следующее определение оправдано замечанием после задачи 3 п.3.2.2 Части I.

является критической точкой f как функции двух действительных переменных и что сохраняются углы между кривыми, проходящими через эту точку, см. определение 3 п.2.6 Части I. Следующие затем теоремы 1 и 2 доказывают равносильность конформности и наличия ненулевой производной: f0(z0) 6= 0. Для ¾исключительных¿ точек 1 и b определение конформности упрощается естественным образом.

О п р е д е л е н и е 4.1.3. Функция f называется конформной в точке 1 (в точке b), если она сохраняет углы между кривыми в точке 1 и их образами в точке a (в точке b и их образами в точке 1).

Т е о р е м а 4.1.2. Дробно-линейная функция (4.1) конформна во всех

точках C.

Т е о р е м а 4.1.3. Если c 6= 0, то дробно-линейная функция (4.1) голоморфна в точке 1.

что означает голоиорфность в 0 и, следовательно, ' в 1.

Т е о р е м а 4.1.4. Композиция дробно-линейных функций '2 '1 есть дробно-линейная функция.

Д о к а з а т е л ь с т в о. Непосредственно проверяем:

Каждой дробно-линейной функции сопоставим матрицу её коэффициен-

тов

a b

cd

Эта матрица невырождена в силу определения дробно-линейной функции. Из доказательства предыдущей теоремы следует, что композиции дробнолинейных функций '2 '1 соответствует произведение их матриц в том же порядке, так как матрица дробно-линейной функции в правой части есть

Т е о р е м а 4.1.5. Обратная к дробно-линейной функции есть дробнолинейная функция.

За м е ч а н и е 4.1.1. Поскольку коэффициенты дробно-линейной функции определены с точностью до постоянного множителя, то можно опустить числовой множитель перед обратной матрицей.

За м е ч а н и е 4.1.2. Поскольку очевидна ассоциативность композиции дробно-линейных функций, равно как и то, что тождественное отображение является дробно-линейным, можно заключить, что множество всех дробнолинейных функций образует группу с операцией композиция. Подробности см., например, в [10, §3].

Круговое свойство стереографической проекции, см. теорему 1 п.3.2.2 Части I, подсказывает следующее определение.

О п р е д е л е н и е 4.1.5. Окружностью на C называется окружность в обычном смысле слова или прямая.

Следующее свойство дробно-линейных функций называется круговым.

ность на C в окружность на C.

6ГЛАВА 4. НЕКОТОРЫЕ КЛАССЫ ГОЛОМОРФНЫХ ФУНКЦИЙ

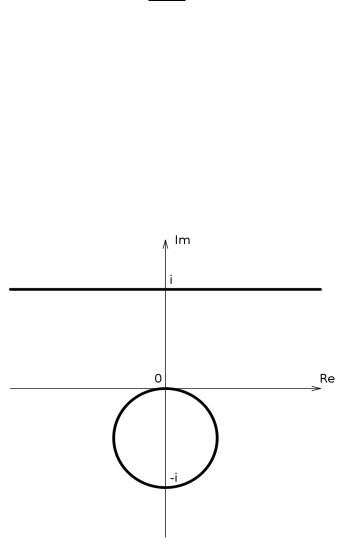
З а д а ч а 4.1.3. Что является образом прямой, параллельной действительной оси и пересекающей мнимую в точке i, при отображении w = z1 ?

Р е ш е н и е. На указанной прямой лежат точки, чьи координаты имеют вид x + i, где x любое действительное число. Координаты точек образа этой прямой имеют вид

Зная, что образом этой прямой должна быть окружность, рассмотрим сумму квадратов действительной и мнимой частей:

Прямая и её образ изображены на рис. 4.1.

З а м е ч а н и е 4.1.3. В точку i окружности перешла точка 1.

Рис. 4.1. Образ прямой Im z = 1 при отображении z1 .

Дальнейшие сведения о дробно-линейных функциях можно почерпнуть из, например, [4, Глава 3], [10, §3].

4.2Степенн´ая функция

О п р е д е л е н и е 4.2.1. Функция f(z) = zn; n 2 N, называется степенн´ой.

Если n = 1, то функция является тождественным отображением, так что полагаем n > 1.

Т е о р е м а 4.2.1. Степенная функция конформна в C n f0g. В точке 0 углы не сохраняются ни при каком n > 1.

Д о к а з а т е л ь с т в о. Производная (zn)0 = nzn 1 6= 0, поэтому первое утверждение теоремы справедливо.

Перепишем степенную функцию в тригонометрическом виде

( (cos ' + i sin '))n = n(cos(n') + i sin(n'))

Отсюда следует, что при возведении в степень n аргумент z увеличивается в n раз, то есть угол с вершиной в 0 не сохраняется.

Степенная функция не является однолистной (см. определение 1, п.2.1, Часть I) при n > 1. Более того, существует ровно n различных чисел, чья n-ая степень равна z = (cos ' + i sin '): модули этих чисел равны

рис.4.2, на котором показано также, как преобразуется координатная сетка при обратном преобразовании она переходит в семейство ортогональных кривых.

Рис. 4.2. Преобразование декартовой сетки

З а д а ч а 4.2.1. Является ли степенная функция f(z) = zn конформной в 1?

Р е ш е н и е. Так как f(1) = 1, то из определения 4.1.3 следует, что

конформность f в точке 1 равносильна сохранению углов в 0 композицией

, где (z) = z1 . Но (z) = zn при n > 1 не сохраняет углы в 0, поэтому степенная функция не является конформной в 1.

8ГЛАВА 4. НЕКОТОРЫЕ КЛАССЫ ГОЛОМОРФНЫХ ФУНКЦИЙ

4.3Функция Жуковского

О п р е д е л е н и е 4.3.1. Функция (z) = 12 z + z1 называется функцией Жуковского.

Название обязано её роли в аэродинамических расчётах, проведённых Н.Е.Жуковским.

Найдём, прежде всего, области однолистности.

У т в е р ж д е н и е 4.3.1. Областью однолистности в C является любая область, для двух любых точек z1; z2 которой выполняется условие z1z2 6= 1.

два корня (считая кратности). Если имеется корень z , то, очевидно, корнем будет и z = z1 . Следовательно, любая область, для двух любых точек z1; z2 которой выполняется условие z1z2 6= 1, является областью однолистности .

С л е д с т в и е. В C такими областями являются, например, открытый (то есть без граничной окружности) единичный круг D = fz : jzj < 1g и внешность замкнутого (то есть с граничной окружностью) единичного

Д о к а з а т е л ь с т в о. (z) 6= 1 для любого z 2 D; z 6= 0 и (0) = 1, так что в D

Т е о р е м а 4.3.1. Функция Жуковского : C ! C конформна в Cnf 1; 1g.

З а м е ч а н и е 4.3.1. Функция удваивает углы в точках 1, см., например, [4, гл.3, §10], [10, §3].

!

Т е о р е м а 4.3.2. Функция Жуковского : C C осуществляет взаимнооднозначное конформное отображение как внешности D0 замкнутого еди-

n

ничного круга, так и открытого единичного D круга на C [ 1; 1].

4.4Показательная функция

О п р е д е л е н и е 4.4.1. Показательной функцией или экспонентой

Прежде всего, выясним, при каких z существует этот предел.

Пусть z = x + iy, тогда модуль выражения под знаком предела можно переписать так:

10 ГЛАВА 4. НЕКОТОРЫЕ КЛАССЫ ГОЛОМОРФНЫХ ФУНКЦИЙ

Д о к а з а т е л ь с т в о. Так как для любой голоморфной функции f справедливо со-

отношение

f0(x + iy) = @ f(x + iy) @x

(см., например, следствие из теоремы 2 п.2.5 Часть I), то

С л е д с т в и е. Показательная функция конформна в C.

Д о к а з а т е л ь с т в о. ez 6= 0 для любого z 2 C, поскольку jezj = ex > 0.

Т е о р е м а 4.4.4. Показательная функция периодична с периодом 2 i.

С л е д с т в и е. Показательная функция однолистна в

D= f2 (n 1) 6 Im z < 2 n; n 2 Zg:

До к а з а т е л ь с т в о. Из доказательства теоремы следует, что для однолистности экспоненты на некотором множестве G достаточно, чтобы для любых z1; z2 2 G было справедливо z1 z2 6= 2 ki; 8k 2 Z. Указанные области D, очевидно, удовлетворяют

такому условию.

З а д а ч а 4.4.1. Доказать, что экспонента взаимно-однозначно отображает D на C n f0g.

Р е ш е н и е. В силу следствия из последней теоремы доказать надо только сюръективность: для всякого w 2 Cnf0g найдётся такое z 2 D, что ez = w. Но если w = (cos ' + i sin '), то в качестве z возьмём ln + i(' + 2 (n 1))

З а д а ч а 4.4.2. Найти jea+ibj:

О т в е т. ea.

4.5Тригонометрические функции

оправдывают следующее определение, которое голоморфно продолжает эти тригонометрические функции в C.

Областью определения sin z; cos z является, очевидно, C. Функции tg z и ctg z определены всюду, кроме тех точек, в которых cos z = 0 и sin z = 0 соответственно.

Свойства тригонометрических функций

Т е о р е м а 4.5.1. Каждая из функций sin z; cos z; tg z; ctg z голоморфна в своей области определения.

Д о к а з а т е л ь с т в о. Это сразу следует из определения 4.5.1, теоремы 4.4.2 и теоремы 1 п.2.5, Часть I.

З а д а ч а 4.5.1. Проверить соотношения

sin2 z + cos2 z = 1;

sin(z1 + z2) = sin z1 cos z2 + cos z1 sin z2; cos(z1 + z2) = cos z1 cos z2 sin z1 sin z2; sh z = i sin iz; ch z = cos iz;

sin z = i sh iz; cos z = ch iz

для всех z 2 C.

З а д а ч а 4.5.2. Найти действительные и мнимые части sin(a + ib); cos(a + ib):

О т в е т. sin a ch b + i cos a sh b; cos a ch b i sin a sh b. З а д а ч а 4.5.3. Найти

j sin(a + ib)j; j cos(a + ib)j:

О т в е т. sin2 a + sh2 b; cos2 a + ch2 b.