
Математика. Комплексный анализ, часть 2
.pdfГлава 7
Элементы операционного исчисления
7.1Оригиналы и изображения
Операционноое исчисление есть набор методов для решения дифференциальных и интегральных уравнений путём сведения их к алгебраическим уравнениям; последние во многих случаях решаются проще. Для такого сведения используется одностороннее преобразование Лапласа функций, растущих не быстрее экспоненты. Если удаётся решить получившуюся алгебраическую задачу, то обратное преобразование Лапласа предоставляет решение исходной задачи.
Перейдём к точным формулировкам.
О п р е д е л е н и е 7.1.1. Функцией-оригиналом называется комплекснозначная функция f действительного аргумента t, удовлетворяющая следующим условиям:
(1)f кусочно-непрерывная функция;
(2)f является тождественным нулём на отрицательной полуоси;
(3)f растёт не быстрее экспоненты, то есть существуют такие константы C > 0; > 0, что для всех t > 0 справедливо
jf(t)j < Cet:
П р и м е р 7.1.1. Следующие функции являются оригиналами.
f(t) = |
( t3; |
если t > 0 |
f(t) = |
( t2e2t; |
если t > 0 |
|
0; |
если t < 0 |
|
0; |
если t < 0 |
Функция |
|
|
|
|
|
43

44 ГЛАВА 7. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
(
0; если t < 0
f(t) =
et3 ; если t > 0
оригиналом не является (почему?).
З а м е ч а н и е 7.1.1. В дальнейшем всегда будем подразумевать, что оригинал равен 0 на отрицательной полуоси и не будем упоминать об этом каждый раз.
О п р е д е л е н и е 7.1.2. Односторонним преобразованием Лапласа opигинала f называется функция комплексного переменного p
|
+1 |
|
|
F (p) = |
Z |
f(t)e pt dt |
(7.1) |
|
0 |
|
|
Функция F называется также изображением оригинала f.
Корректность определения, то есть сходимость интеграла в (7.1) при Re p > следует из третьего условия в определении 7.1.1.
Т е о р е м а 7.1.1. Если f(t) F (p), то
|
lim |
F (p) = 0: |
(7.2) |
|
|
Re p!+1 |
|
|
|
Д о к а з а т е л ь с т в о. Из определения оригинала следует |
|
|||
+1 |
+1 |
|
|
|
jF (p)j 6 Z0 |
je ptjjf(t)j dt 6 C Z0 e( Re p+ )t dt = Re p ; |
|
||
|
|
|
C |
|
откуда следует (7.2).
Доказательство следующего факта можно прочитать, например, в [4, Глава VI, п.10].
Т е о р е м а 7.1.2. Если f(t) F (p), то функция F (p) является голоморфной в полуплоскости fp 2 C : Re p > g и её производные доставляются формулой
|
+1 dn |
|
|
|
F (n)(p) = |
Z0 |
dpn e ptf(t) dt; |
n 2 N: |
(7.3) |
То, что функция F (p) является изображением оригинала f(t) записывается так:
f(t) F (p):
П р и м е р 7.1.2. Изображением оригинала e2t является функция
+1
Z
F (p) = e2te pt dt:
0

7.2. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА |
45 |
Интеграл сходится в полуплоскости Re p > 2, поэтому
1
F (p) = p 2:
Символическая запись:
e2t p 1 2:
За м е ч а н и е 7.1.2. Поскольку мы ограничимся только односторонним преобразованием Лапласа, слово "одностороннее" будем опускать.
За д а ч а 7.1.1. Найти изображения следущих оригиналов:
(1)f(t) = t;
(2)f(t) = sin t;
(3)f(t) = et.
Р е ш е н и е.
|
+1 |
|
te pt |
+1 |
1 |
+1 |
|
e pt |
+1 |
1 |
|
||||||||
(1) |
Z |
te pt dt = |
|
|
|
0 |
|
+ |
|
Z |
e pt dt = |
|
0 |
|
= |
|
; Re p > 0: |
||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
+1sin t e pt dt = cos t e pt +1 |
p |
+1cos t e pt dt = 1 |
|||||||||||||||
|
|
Z |
|
|
|
|
|
|
|
|
|
0 |
|
Z |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0sin t e pt |
+ |
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
p |
0 |
1 |
+ p Z |
1sin t e pt dt1 |
= 1 p2 |
Z |
1sin t e pt dt; |
||||||||||||
|
@ |
|
|
|
|
|
0 |
|
|
|
|
A |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть
|
|
sin t |
1 |
|
; |
|
Re p > 0: |
|||
|
|
|
|
|||||||
|
Z |
1 + p2 |
0 |
|||||||
(3) |
et e pt dt = e1 |
p |
1 |
= p |
1 |
1; Re p > 1: |
||||
|
+1 |
(1 |
p)t |
+ |
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Вдальнейшем мы будем (как правило) опускать упоминание Re p > .
7.2Свойства преобразования Лапласа
Следующие две теоремы сразу следуют из (7.1).

46 ГЛАВА 7. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Линейность и подобие
Т е о р е м а 7.2.1. Изображение линейной комбинации оригиналов есть линейная комбинация их изображений:
f(t) + g(t) ! F (p) + G(p):
Следующая теорема называется теоремой подобия.
Т е о р е м а 7.2.2. Для любой вещественной константы k > 0 справедливо
f(kt) k1 F kp :
З а д а ч а 7.2.1. Найти изображение функций sin !t; e t.
Р е ш е н и е. Из теоремы подобия и задачи (7.1.1)следует
sin !t |
1 |
|
|
|
|
1 |
|
= |
! |
|
; |
||
|
|
|
|
|
|
|
|
|
|
||||
! 1 + |
!p 2 |
!2 + p2 |
|||||||||||
e t |
1 |
|
|
|
1 |
|
= |
1 |
: |
|
|||
|
|
|
p 1 |
|
p |
|
|||||||
Дифференцирование оригинала и изображения
Преобразование Лапласа переводит операцию дифференцирования в "безобидные" операции умножения на аргумент и вычитания констант!
З а м е ч а н и е 7.2.1. В следующей теореме предполагается, что если 0 точка разрыва оригинала или какой-либо его производной, то под значением функции в 0 подразумевается предел при t ! 0 справа.
Также будем предполагать, что если производная g0(t) является оригиналом, то сама функция g(t) непрерывна.
Т е о р е м а 7.2.3. Если функции f(t); f0(t); : : : ; f(n)(t) суть оригиналы и
f(t) F (p), то
f0(t) pF (p) f(0);
f00(t) p2F (p) pf(0) f0(0);
: : :
f(n)(t) pnF (p) pn 1f(0) pn 2f0(0) f(n 1)(0):
Д о к а з а т е л ь с т в о. Интегрируем по частям:
+1f0(t)e pt dt = f(t)e pt +1 |
|
Z |
0 |
0 |
|
|
|
|
|
Далее по индукции.
+1
Z
+ p f(t)e pt dt = f(0) + pF (p):
0
З а д а ч а 7.2.2. Найти изображение функции cos t.
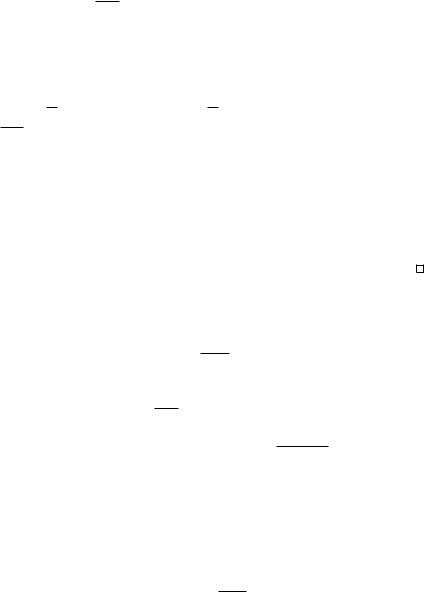
7.2. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА |
47 |
|||||
Р е ш е н и е. Так как sin t |
1 |
, см. задачу 7.1.1, то |
||||
p2+1 |
||||||
1 |
|
p |
|
|||
cos t = sin0 t p |
|
0 = |
|
: |
||
p2 + 1 |
p2 + 1 |
|||||
З а д а ч а 7.2.3. Найти изображение функции sin2 t.
Р е ш е н и е. Обозначим искомое изображение через F (p). Так как (sin2 t)0 = 2 sin t cos t = sin 2t p22+4 , то из теоремы 7.2.3 следует
2 |
= p F (p) 0; |
2 |
|
|
|
||
|
|
F (p) = |
|
|
|
: |
|
p2 + 4 |
p(p2 + 4) |
||||||
З а д а ч а 7.2.4. Найти изображение tn; n 2 N. |
|
||||||
Р е ш е н и е. Из задачи 7.1.1 следует, что (t2)0 = 2t |
2 |
. Из теоремы 7.2.3 |
|||||
p2 |
|||||||
следует, что p22 pF (p), то есть t2 p23 . Применяя индукцию, получаем
tn pnn+1! .
Производная изображения есть изображение оригинала, умноженного
на t. |
7.2.4. Если F (p) f(t), то F (n)(p) ( t)nf(t). |
||||||||||||
Т е о р е м а |
|||||||||||||
Д о к а з а т е л ь с т в о. Из (7.3) следует, что |
|
|
|
||||||||||
|
|
|
|
+1 |
|
|
|
|
|
|
|
||
|
F 0(p) = |
Z0 |
|
( t)e ptf(t) dt ( t)f(t): |
|
||||||||
Далее по индукции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а |
7.2.5. Найти изображение функции tet. |
|
|||||||||||
Р е ш е н и е. Так как et |
1 |
|
, то |
|
|
|
|
|
|||||
p |
1 |
p 1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
(p 1)2 |
|
||||||
|
t et = ( |
|
t)( |
|
et) |
|
1 |
|
= |
1 |
: |
||
|
|
|
|
|
|
||||||||
З а д а ч а |
7.2.6. Найти изображение функции t2 cos t. |
|
|||||||||||
Р е ш е н и е. Так как cos t p2p+1 , то из теоремы 7.2.4 следует
t2 cos t = ( |
|
t)2 cos t |
|
p |
|
00 |
= |
2p3 6p |
: |
|
p2 + 1 |
|
|
(1 + p2)3 |
|||||
|
|
|
|
|
|||||
Интегрирование оригинала и изображения
Преобразование Лапласа переводит операцию интегрирования в операцию деления на аргумент.
Т е о р е м а 7.2.5. Если f(t) F (p), то
t
Z
f( ) d F p(p):
0

48 |
ГЛАВА 7. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ |
||||
|
|
t |
|
|
|
З а д а ч а |
|
R |
sin d . |
||
7.2.7. Найти изображение |
|||||
|
|
0 |
|
|
|
Р е ш е н и е. Из теоремы 7.2.5 сразу следует |
|||||
|
Z0 |
t |
p2 + 1: |
||
|
sin d p |
||||
|
|
1 |
|
1 |
|
Доказательство следующей теоремы можно найти, например, в [6, §47] .
Т е о р е м а 7.2.6. Если f(t) F (p) и функция f(t)=t является оригиналом,
|
R |
f(t) |
|
R |
то интеграл |
+1F (p) dp сходится и |
t |
|
1F (s) ds, где интегрирование |
|
p |
|
|
p |
ведётся по пути , такому, что Re > ; Re ! +1.
З а м е ч а н и е 7.2.2. Эта теорема допускает более общую формулировку, см., например, [3, §11].
С л е д с т в и е. Если дополнительно к условиям теоремы сходится интеграл
+1
R f(tt) dt, то справедливо
0
+1 |
|
+1 |
|
Z f t |
dt = Z |
F (s) ds |
|
|
(t) |
|
|
00
(оба интеграла берутся по положительной полуоси).
Теорема 7.2.6 позворляет легко вычислять некоторые несобственные интегралы.
|
|
+1 |
|
|
|
|
|
||
З а д а ч а 7.2.8. Вычислить |
|
R1 |
|
sin t |
dt. |
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
t |
|
|
||
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Р е ш е н и е. Так как sin t |
|
, то |
|
|
|||||
p2+1 |
|
|
|||||||
+1 |
t dt = |
+1 |
s2 + 1 |
+1 |
= 2 : |
||||
Z |
Z |
= arctg s 0 |
|||||||
0 |
sin t |
0 |
|
|
ds |
|
|
||
Теоремы запаздывания и смещения
Функцию f(t ), где некоторая положительная константа, можно интерпертировать как ту же функцию с "запаздыввание на время ". Подобная ситуация часто встречается в математических моделях управляемых систем, когда внешнее воздействие влияет на систему с некоторой задержкой. Преобразование Лапласа превращает операцию запаздывания в умножение на константу.
Т е о р е м а 7.2.7. ("теорема запаздывания"). Если f(t) F (p), то
f(t ) e p F (p)
для любого > 0 (напомним, что f(s) = 0 при s < 0).
7.2. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА |
49 |
Д о к а з а т е л ь с т в о. Так как
+1
Z
f(t ) e ptf(t ) dt;
0
то, делая замену s = t и учитывая условие (2) в определении 7.1.1, получаем
+1 |
+1 |
ZZ
e ptf(t ) dt = e ps p f(s) ds = e p F (p):
Аналогично, смещение изображения равносильно умножению оригинала на (комплексную) константу.
Т е о р е м а 7.2.8. ("теорема смещения").
Если f(t) F (p), то eqtf(t) F (p q) для любого q 2 C.
Д о к а з а т е л ь с т в о. Сразу следует из (7.1).
За м е ч а н и е 7.2.3. Эту теорему называют также "теоремой затухания", так как при Re q < 0 множитель eqt ! 0 при t ! +1.
За д а ч а 7.2.9. Найти изображения следующих функций.
(1) sin(t |
|
a); |
(2) e t sin t: |
|
Р е ш е н и е. (1) Из теоремы запаздывания сразу следует
|
1 |
|
|
|
sin(t a) e ap |
|
: |
||
p2 + 1 |
||||
(2) Из теоремы смещения следует |
|
|
|
|
e t sin t |
1 |
|
: |
|
|
||||
(p + )2 + 1 |
||||
З а д а ч а 7.2.10. Найти изображения оригиналов, чьи графики представлены на рис.7.1.
(1) |
(2) |

50 ГЛАВА 7. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
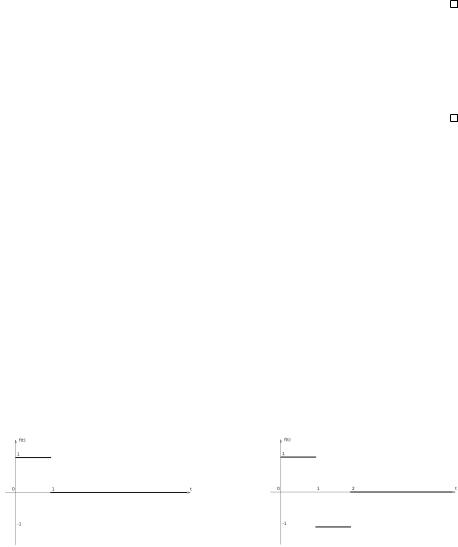
(3)
Рис. 7.1
Ре ш е н и е.
1.Обозначим через h(t) функцию-оригинал, равную 1 при неотрица-
тельных t. Тогда функция f1, чей график изображён на рис. 7.1, может
быть представлена в виде f1(t) = h(t) h(t 1). Далее, очевидно, что h(t) p1 . Из свойства линейности преобразования Лапласа и теоремы за-
|
|
f |
(t) |
1 |
|
e p 1 |
= 1 e p |
|
||||||
паздывания получаем |
1 |
|
|
p |
p |
|
p . |
|
||||||
2. |
Данную функцию можно представить как f2(t) = h(t) 2h(t 1) + |
|||||||||||||
h(t 2). Поэтому искомое изображение есть |
|
|||||||||||||
|
|
1 |
|
|
2 |
e p |
|
+ |
e 2p |
|
= |
(1 e p)2 |
: |
|
|
|
p |
p |
p |
p |
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
3. |
Данная функция f3(t) может быть представлена в виде f2( ) d . Из |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
теоремы об интегрировании оригинала 7.2.5 и предыдущего пункта следует
(1 e p)2 f3(t) p2 :
Рис. 7.2

7.2. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА |
51 |
Теорема о свёртке
Пусть f; g некоторые оригиналы.
О п р е д е л е н и е 7.2.1. Свёрткой f и g называется функция
t
Z
(f g)(t) = f( )g(t ) d :
0
Из определения 7.1.1 следует, что свёртка оригиналов есть оригинал. Также очевидно (надо сделать замену = t ), что f g = g f .
Оказывается, свёртке оригиналов соответствует произведение изображений.
Те о р е м а 7.2.9. Если f F; g G, то f g F G. Доказательство можно найти, например, в [6, §47] .
|
|
|
|
|
|
|
t |
|
|
|
1 |
|
1 |
|
'(t) = (t )e d |
|
|||||
|
|
|
1R |
|
. |
|||||
З а д а ч а 7.2.11. Найти изображение функции |
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
Р е ш е н и е. Так как t |
|
; |
e t |
|
, то '(t) |
|
. |
|
|
|
p2 |
p+1 |
p2(p+1) |
|
|
||||||
В следующей таблице приведены изображения часто встречающихся оригиналов.
1 |
1 |
|
|
|
|
|
|
t |
|
1 |
|
|
|
|
|
|
n |
|
|
|
|
n! |
|
|
|
|
|
|
|
n t |
|
|
n! |
|
|
|
|
|
|||
|
|
p |
|
|
|
|
|
e |
|
|
|
p |
|
|
|
|
t |
|
|
|
|
pn+1 |
|
|
t |
e |
|
(p )n+1 |
|||||||||||||
sin t |
|
|
|
|
|
|
|
cos t |
|
p |
|
|
|
|
e t sin t |
|
|
|
|
|
|
|
|
|
|
|
e t cos t |
|
|
p 2 |
|
|
|||||||||
|
|
2 |
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
2 |
+ |
2 |
|
|
|
2 |
|
||||||||||||||||||
|
|
p + |
|
|
|
|
|
|
|
p + |
|
|
|
|
|
|
|
|
(p ) |
|
|
|
|
(p ) + |
|
|
|
||||||||||||||
|
|
|
2p |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
||||
t sin t |
|
|
|
|
|
|
t cos t |
p2 2 |
|
|
|
|
sh t |
|
|
|
|
|
|
|
ch t |
|
|
|
|
|
|
|
|||||||||||||
|
|
2 2 |
) |
2 |
|
) |
2 |
|
2 |
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
||||||||||||||||||||
|
|
(p + |
|
|
|
|
|
(p + |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|||||||||||
Восстановление оригинала по изображению
До сих пор мы искали изображение по заданному оригиналу. А как найти оригинал по известному изображению? Будем, как и прежде, обозначать оригинал через f(t), а его изображение через F (p). Доказательство следующей теоремы можно найти, например, в [6, §48] .
Т е о р е м а 7.2.10. ("обратное преобразование Лапласа"). Если оригинал f(t) непрерывен в точке t и имеет в ней конечные односторонние производные, то справедлива формула
2 i N!+1 |
a+iN |
||
Z |
|||
f(t) = |
1 |
lim |
eptF (p) dp; |
|
|||
a iN
где a любое действительное число, большее .

52 ГЛАВА 7. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
На практике чаще применяются другие способы нахождения оригинала по изображению, см., например, [6, §48] . Приведём одну из формулировок "2-й теоремы разложения" (подробнее см. там же).
Т е о р е м а 7.2.11. Пусть F (p) = Q(p) есть правильная рациональная
R(p)
дробь, то есть Q; R многочлены и степень знаменателя больше степени числителя. Пусть p1; p2; : : : ; pn суть полюсы F . Тогда оригиналом F явля-
ется функция
n
X
f(t) = res(F (p)ept):
pk
k=1
З а д а ч а 7.2.12.
Р е ш е н и е.
7.3Решение задачи Коши
З а д а ч а 7.3.1. Решить задачу Коши
x + x = e t; x(0) = 1:
Р е ш е н и е.
З а д а ч а 7.3.2. Решить задачу Коши
x• + 2x |
|
3x = e t; x(0) = 1; x(0) = 1: |
|
|
Р е ш е н и е.
7.4Элементы теории устойчивости
7.4.1Понятие об устойчивости
Важный вопрос об устойчивости решений системы линейных обыкновенных дифференциальных уравнений
x = Ax;
где A квадратная матрица n-го порядка, сводится к исследованию расположения корней характеристического уравнения
jA Ej = 0:
Именно, решения такой системы асимптотически устойчивы тогда и только тогда, когда все корни характеристического уравнения имеют отрицательные вещественные части. Подробности можно выяснить, например, в [2, Глава 2, §8].
