
Математика. Комплексный анализ, часть 2
.pdf5.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА И ЕГО ПРОСТЕЙШИЕ СВОЙСТВА13
и функцию f(z) = z2. Тогда из (5.1.1) следует |
|
|
|
|
|
|
|||||||
f(z) dz = |
2 r2ei2tireit dt = ir3 2 ei3t dt = r33 ei3t 2 |
= r33 |
(ei6 1) = 0: |
||||||||||
Z |
|
Z |
|
Z |
0 |
|
|
|
|
|
|||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и м е р |
|
|
|
|
|
|
|
|
|
|
|
1 |
. Тогда |
5.1.2. Возьмём ту же окружность и функцию f(z) = |
z |
||||||||||||
|
|
Z |
2 |
|
|
2 |
dt = 2 i: |
|
|
|
|||
|
|
f(z) dz = Z0 |
reit rieit dt = i Z0 |
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Т е о р е м а 5.1.1. Если кусочно-гладкий путь 1 : [ 1; 1] ! C кусочногладко эквивалентен пути 2 : [ 2; 2] ! C (см. определение 7 п.1.2, Часть I), то для любой непрерывной на 1 функции f справедливо
ZZ
f(z) dz = f(z) dz:
1 2
Сформулированная теорема позволяет говорить об интеграле вдоль кривой, см. определения 8, 9 п.1.2, Часть I.
Свойства интеграла вдоль кривой
Т е о р е м а 5.1.2. Пусть функции f; g непрерывны на кусочно-гладкой кривой , пусть ; произвольные комплексные числа. Тогда
Z Z Z
( f(z) + g(z)) dz = f(z) dz + g(z) dz:
Это свойство называется линейностью интеграла. Доказательство сразу следует из определения 5.1.1.
Т е о р е м а 5.1.3. Пусть 1; 2 кусочно-гладкие кривые, причём конец1 совпадает с началом 2 и объединение = 1 [ 2 этих кривых не имеет самопересечений (кроме, возможно, совпадения начальной точки кривой 1 с конечной точкой кривой 2). Тогда для любой непрерывной на функции f справедливо
Z Z Z
f(z) dz = f(z) dz + f(z) dz:
1 2
Это свойство называется аддитивностью интеграла.
З а м е ч а н и е 5.1.1. В доказательстве не используется тот факт, что s1( 2) = s2( 2). Поэтому теорема верна и для кривых, объединение которых не является непрерывной кривой.

14 |
ГЛАВА 5. ИНТЕГРИРОВАНИЕ |
З а м е ч а н и е 5.1.2. Если объединение кривых 1 [ 2 имеет самопересечения, то его можно разбить на несколько несамопересекающихся кривых, сохраняя при этом направление обхода. Применяя доказанную теорему несколько раз к получившимся кривым, находим, что она справедлива и в этом случае. Так что от требования отсутствия самопересечений можно отказаться. Например, на рис. 5.1 интеграл по кривой представляетсяв виде суммы интегралов по кривым AM; MBM; MC.
1 |
2 |
= 1 [ 2 |
Рис. 5.1. Самопересекающаяся кривая .
Т е о р е м а 5.1.4. Пусть кусочно-гладкая кривая. Обозначим черезту же кривую с другим направлением обхода, см. определение 8 п.1.2, Часть I. Тогда для любой непрерывной на функции f справедливо
ZZ
f(z) dz = f(z) dz:
Это свойство называется ориентированностью интеграла.
Т е о р е м а 5.1.5. Пусть кусочно-гладкая кривая. Тогда для любой непрерывной на функции f справедливо неравенство
Z
j f(z) dzj 6 Mj j; (5.2)
где M = max jf(z)j; j j есть длина кривой .
z2
З а д а ч а 5.1.1. Вычислить R (z a)n dz; n 2 Z, где окружность
радиуса r с центром в точке a.
Р е ш е н и е. Окружность радиуса r с центром в точке a можно параметризовать так:
(t) = a + reit; t 2 [0; 2 )
(то есть указанный путь является представителем кривой). Тогда
|
2 |
|
2 |
|
Z |
(z a)n dz = Z0 |
rneintireit dt = irn+1 |
Z0 |
ei(n+1)t dt: |

5.2. ПЕРВООБРАЗНАЯ |
|
|
|
|
15 |
|||
Пусть n 6= 1, тогда последний интеграл равен |
|
|||||||
|
|
|
i(n + 1)ei(n+1)t |
2 |
|
|||
|
|
|
= 0: |
|
||||
|
|
|
irn+1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
Если же n = 1, то |
|
irn+1 Z0 |
|
|
|
|
||
|
|
ei(n+1)t dt = 2 i: |
|
|||||
Таким образом, имеет место замечательное соотношение |
|
|||||||
Z |
|
|
|
|
2 i; |
если n = 1: |
|
|
(z |
|
a)n dz = |
|
|
0; |
если n 6= 1; |
(5.3) |
|
З а д а ч а 5.1.2. Вычислить
Z
zn dz; n 2 Z; n 6= 1;
L
где L кусочно-гладкая кривая, соединяющая точки z1; z2 и не проходящая через 0.
Р е ш е н и е. Параметризуем кривую L, то есть выберем какой-либо путь: [ ; ] ! C, являющийся её представителем. Тогда
Z Z
zn dz = n(t) 0(t) dt = n +1 1( n+1( ) n+1( )) = n +1 1(z1n+1 z2n+1):
Таким образом, этот интеграл зависит только от начальной и конечной точек, но не от вида кривой. В частности, для любой замкнутой кривой, не проходящей через 0, он равен 0.
5.2Первообразная
О п р е д е л е н и е 5.2.1. Первообразной функции f в области G называется голоморфная в G функция F такая, что
F 0(z) = f(z) |
z |
2 |
D: |
(5.4) |
8 |
|
|
Пр и м е р 5.2.1. Функция z3 + 4z + 2 является первообразной для 3z2 + 4 в C.
Пр и м е р 5.2.2. Функция z1 является первообразной для z12 в C n f0g.
Как и в действительном анализе, прибавляя к какой-то первообразной данной функции константы, мы получим все первообразные зтой функции.

16 |
ГЛАВА 5. ИНТЕГРИРОВАНИЕ |
Т е о р е м а 5.2.1. Если F первообразная для f, то все первообразные функции f предоставляются формулой F (z) + C; 8C 2 C.
Вопрос о существовании первообразной оказывается более сложным, нежели в действительном случае. Это связано с вещественной двумерностью C.
5.3Теоремы Коши
Рассмотрим какую-нибудь функцию f, голоморфную в области D и произвольный треугольник D. Треугольники понимаются здесь как треугольные области, дополненные своими границами (см., например, п.1.2, Часть I). Ориентируем границу треугольника так, чтобы при её обходе треугольник оставался всё время с одной стороны. Такой треугольник будем называть ориентированным. Имеет место следующее утверждение, являющееся простой формой теоремы Коши.
Т е о р е м а 5.3.1. В этих условиях справедливо равенство
Z
f(z) dz = 0: |
(5.5) |
Доказанная теорема позволяет установить существование первообразной для голоморфной в некотором круге функции.
Т е о р е м а 5.3.2. Пусть U круг радиуса r с центром в точке a, функция f голоморфна в U. Обозначим через [a; z] отрезок прямой, соединяющий центр круга с произвольной внутренней точкой z. Тогда функция
Z
F (z) = f( )d
[a;z]
является первообразной для f.
З а м е ч а н и е 5.3.1. В приведённом доказательстве тот факт, что непрерывная функ-
ция f является голоморфной, использовался лишь для обоснования равенства R1 |
f( )d = |
R |
|
0. Поэтому теорема верна для любой непрерывной в U функции f такой, что f( )d = 0
для любого ориентированного треугольника U.
З а д а ч а 5.3.1. Найти первообразную функции z1 в открытом круге U = fjz 1j < 1g. Р е ш е н и е. Из только что доказанной теоремы следует, что функция
Z 1
F (z) = d
[1;z]
будет первообразной. Интегрирование производится по отрезку [1; z], см. рис. 5.2. Параметризуем отрезок [1; z] так:
(t) = 1 + t cos + it sin ; 0 6 t 6 ;
где через обозначена длина отрезка [1; z]. Тогда 0(t) = cos + i sin и из определения
5.1 следует, что
Z
cos + i sin
F (z) = |
|
dt: |
|
||
|
1 + t cos + it sin |
|
0

5.3. ТЕОРЕМЫ КОШИ |
17 |
Рис. 5.2
Преобразуем подынтегральное выражение: |
|
|
|
|
|
|
|||||||||||||||
|
|
cos + i sin |
= |
|
(cos + i sin )(1 + t cos it sin ) |
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 + t cos + it sin (1 + t cos + it sin )(1 + t cos it sin ) |
||||||||||||||||||||
|
|
|
|
|
|
t + cos |
|
|
|
|
|
sin |
|
|
|
||||||
= |
|
|
|
|
|
|
+ i |
|
|
|
= |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 + t2 + 2t cos 1 + t2 |
+ 2t cos |
|
|
|
||||||||||||
|
|
|
|
|
t + cos |
|
|
|
|
|
|
sin |
|
|
|
||||||
|
= |
|
|
+ i |
|
|
: |
|
|
|
|||||||||||
|
(t + cos )2 + sin2 |
(t + cos )2 + sin2 |
|
|
|
||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(t + cos )2 + sin2 |
dt: |
|||||||||
|
F (z) = Z0 (t + cos )2 |
+ sin2 dt + i Z0 |
|||||||||||||||||||
|
|
|
|
|
t + cos |
|
|
|
|
|
|
sin |
|
|
|
||||||
Первый из этих интегралов равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
ln( 2 + 2 cos + 1) = |
1 |
ln(( cos + 1)2 + 2 sin2 ) = ln r; |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
см. рис. 5.2. Второй интеграл равен
arctg |
+ cos |
arctg(ctg ): |
sin |
Из очевидного соотношения
x + y arctg x + arctg y = arctg 1 xy
следует, что второй интеграл равен
01
|
|
+cos |
cos |
arctg |
@ |
sin |
sin |
1 + cossin2 |
|||
|
|
|
+cos2 |
см. рис. 5.2, поэтому
sin
A = arctg = arctg(tg ') = '; 1 + cos
F (z) = ln jzj + i':

18 |
ГЛАВА 5. ИНТЕГРИРОВАНИЕ |
Теорема 5.3.2 утверждает наличие первообразной для функции, определённой в области G, лишь локально, в некотором круге. Глобальная первообразная во всей области определения G (понимаемая как функция точки области G) может и не существовать! Однако "склеивая" локальные первообразные, можно получить первообразную вдоль пути.
Пусть функция f определена в области G и пусть задан непрерывный путь : [a; b] !
G.
Оп р е д е л е н и е 5.3.1. Непрерывная функция
: [a; b] ! C
называется первообразной для f вдоль пути , если для любой точки 2 [a; b] существует открытый круг U G с центром в z = ( ), в котором f имеет первообразную FU такую, что
FU ( (t)) = (t)
для всех t из некоторой окрестности .
З а м е ч а н и е 5.3.2. Первообразная вдоль пути является функцией параметра t и может не быть функцией точки z.
Т е о р е м а 5.3.3. Для любой голоморфной в области G функции f и любого непрерывного пути : [a; b] ! C первообразная вдоль существует и определяется с точностью до постоянного слагаемого.
З а м е ч а н и е 5.3.3. Для краткости образ пути ([a; b]) будем также называть путём.
Д о к а з а т е л ь с т в о. Для каждой точки пути существует в силу теоремы 5.3.2 открытый круг с центром в этой точке, в котором f имеет первообразную. Разобьём отрезок [a; b] точками tj; j = 0; 1; : : : ; n на такие мелкие отрезки [tj 1; tj], что круги Uj с центрами в (tj), в которых существует первообразная для f, покрывали весь путь1. Эти круги можно выбрать настолько малыми, что каждый пересекается лишь со своими соседями, см. рис. 5.3. Выберем какую-нибудь первообразную F1 в круге U0; в круге U1 выберем такую первообразную F1, которая совпадает с F0 в U0 \ U1 (все первообразные отличаются постоянным слагаемым), в круге U2 выберем первообразную F2, совпадающую с F1 в U1 \ U2 и продолжим этот процесс до круга Un. В результате первообразная будет построена вдоль всего пути.
Её единственность (с точностью до постоянного слагаемого) следует из того, что любая другая первообразная отличается от построенной на константу в каждом круге и является при этом непрерывной функцией. 
Для первообразной справедлива формула Ньютона-Лейбница.
Т е о р е м а 5.3.4. Для любой функции f, непрерывной и имеющей первообразную вдоль кусочно-гладкого пути : [a; b] ! C, справедливо
Z
f(z) dz = (b) (a):
Д о к а з а т е л ь с т в о. Из определения первообразной вдоль пути следует, что для любой точки пути существует круг с центром в этой точке такой, что в нём существует (обычная) первообразная F , сужение которой на совпадает с . Разобьём путь на гладкие кусочки
j : [tj 1; tj]; t0 = a; tn = b
настолько маленькие, что каждый из них лежит в одном из таких кругов Uj, причём эти круги покрывают весь путь (о возможности выбора такого конечного покрытия см.
1Строго говоря, наличие такого разбиения не является очевидным. Оно следует из свойств непрывной на отрезке функции. Подробности см., например, в [10, §5].
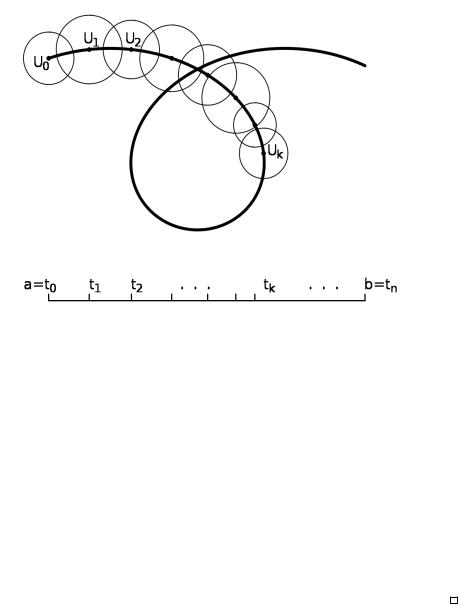
5.3. ТЕОРЕМЫ КОШИ |
19 |
Рис. 5.3. Построение первообразной вдоль пути
доказательство теоремы 5.3.3 ). Через Fj будем обозначать обычную первообразную для f в круге Uj, существующую силу теоремы 5.3.2 . Тогда для любого t 2 [tj 1; tj] справедливо
(t) = Fj( (t)) + Cj;
где Cj некая константа. Поскольку каждый кусочек пути является гладким, функцияоказывается дифференцируемой на [tj 1; tj] (а не только непрерывной, как требова-
лось в определении 5.3.1):
0(t) = f( (t)) 0(t)
и
|
|
tj |
|
tj |
|
Z |
f(z) dz =t |
Z |
f( (t)) 0(t) dt =t |
Z |
0(t) dt = (tj) (tj 1): |
j |
|
j 1 |
|
j 1 |
|
Отсюда следует, что
Zn Z
X
f(z) dz = f(z) dz = (b) (a):
j=1 j
За м е ч а н и е 5.3.4. Не всякая голоморфная функция имеет первообраз-
ную. Например, функция z1 в C n f0g. Для доказательства рассмотрим окружность с центром в 0. Если бы первообразная существовала, то интеграл по этой окружности должен был равняться 0, но это не так, см. задачу 5.1.1.
Теорема 5.3.1 может быть существенно обобщена. Именно, оказывается, что в односвязной области (см. определение 13 п.1.2 Части I) интеграл от голоморфной функции по любому замкнутому пути равен 0. Более того,
20 |
ГЛАВА 5. ИНТЕГРИРОВАНИЕ |
если путь (в необязательно односвязной) области непрерывно деформируется так, что его концы остаются на месте, то интеграл по нему не изменяется.
Перейдём к точным формулировкам.
Пусть в области D имеются два пути с общими концами:
0 : [ ; ] ! D; 1 : [ ; ] ! D; 0( ) = 1( ) = a; 0( ) = 1( ) = b:
О п р е д е л е н и е 5.3.2. Эти пути называются гомотопными, если существует непрерывное отображение (t; s) прямоугольника [ ; ] [0; 1] в D такое, что
(t; 0) 0(t); (t; 1) 1(t); (0; s) a; (1; s) b:
Другими словами, при непрерывном изменении параметра s путь 0 непрерывно деформируется в путь 1. Точки a; b могут совпадать, то есть пути могут быть замкнутыми.
О п р е д е л е н и е 5.3.3. Замкнутый путь
0 : [ ; ] ! D; 0( ) = 0( ) = a
называются гомотопным нулю, если существует непрерывное отображение(t; s) прямоугольника [ ; ] [0; 1] в D такое, что
(t; 0) 0(t); (t; 1) a:
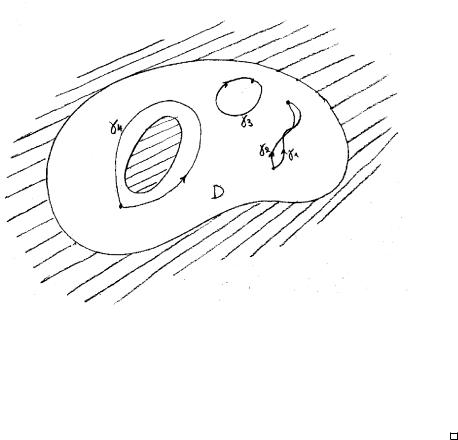
Другими словами, гомотопный нулю путь может быть непрерывно стянут в точку. На рис. 5.4 пути 1 и 2 гомотопны; путь 3 гомотопен нулю; путь 4 не гомотопен нулю.
Примем без доказательства следующее интуитивно понятное утверждение. Интересующиеся строгим доказательством могут узнать его из, например, [7].
У т в е р ж д е н и е 5.3.1. В односвязной области любые два пути с общими концами гомотопны, а любой замкнутый путь гомотопен нулю.
Примем без доказательства следующую теорему Коши. Подробности можно узнать, например, в [4, Глава 5], [10, §5].
Т е о р е м а 5.3.5. Интегралы от голоморфной функции по гомотопным в области D путям равны.
Другими словами, при непрерывной деформации пути с закреплёнными концами интеграл от голоморфной функции по этому пути не изменяется.
Вкачестве следствия получаем ещё одну теорему Коши.
Те о р е м а 5.3.6. Интеграл от голоморфной функции f по замкнутому пути в односвязной области D равен 0.
Д о к а з а т е л ь с т в о. Замкнутый путь 0 в односвязной области D можно непрерывной деформацией перевести в замкнутый путь 1, который целиком лежит в некотором круге U D. Теорема 5.3.2 утверждает, что в этом случае в U имеется первообразная F . Из доказательства теоремы 5.3.3 следует, что первообразная (t) вдоль пути 1
5.3. ТЕОРЕМЫ КОШИ |
21 |
Рис. 5.4
равна F ( 1(t)). А из теоремы 5.3.4 следует, что
Z
f(z) dz = ( ) ( ) = F (a) F (a) = 0:
1
С л е д с т в и е. Всякая голоморфная в односвязной области D функция
fимеет первообразную в этой области.
Внеодносвязной области первообразная может и не существовать, как это следует из замечания 5.3.4. Однако, если неодносвязная область имеет "простой" вид, то справедливо некое обобщение теоремы Коши. Сперва определим, что такое "просто устроенная" область.
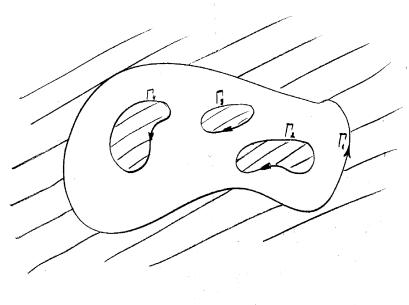
Будем считать, что граница ограниченной области D состоит из конечного числа замкнутых кривых. Внешняя кривая должна быть ориентирована против часовой стрелки, остальные должны быть ориентированы таким образом, что область D остаётся слева при прохождении по этим кривым, см. рис. 5.5.
О п р е д е л е н и е 5.3.4. Совокупность таких кривых называется
ориентированной границей области D.
Обобщённая теорема Коши утверждает, что интеграл от голоморфной функции по ориентированной границе области D равен 0. Область при этом может не быть односвязной.
22 |
ГЛАВА 5. ИНТЕГРИРОВАНИЕ |
Рис. 5.5
Т е о р е м а 5.3.7. Пусть функция f голоморфна в области G, пусть
|
|
[ 2 [ |
ограниченная область D такова, что D G и имеет границу = 1 |
||
: : : [ n в виде конечного числа кривых. Тогда |
|
|
Z |
f(z) dz = 0: |
|
|
|
|
5.4Интегральная формула Коши
Одно из удивительных свойств голоморфных функций состоит в том, что значение такой функции в точке определяется её значениями на границе любой области, содержащей эту точку! Этот факт называется интегральной формулой Коши.
Т е о р е м а 5.4.1. Пусть функция f голоморфна в области D, пусть область G, ориентированная граница которой является объединением конечного числа кривых, лежит вместе с границей в D. Тогда для любой точки z 2 G справедливо
f(z) = 2 i Z |
z d : |
(5.6) |
|
1 |
|
f( ) |
|
Правая часть этой формулы называется интегралом Коши.
