
- •1 Комплексная плоскость
- •1.1 Комплексные числа
- •Задачи
- •1.2 Области, пути и кривые,
- •2 Функции комплексного переменного
- •2.1 Понятие функции
- •2.2 Предел функции
- •2.3 Непрерывность
- •2.4 Линейные функции
- •2.5 Дифференцируемость
- •2.6 Геометрическая интерпретация производной
- •3 Стереографическая проекция
- •3.1 Стереографическая проекция и бесконечность
- •3.2 Свойства стереографической проекции
- •3.2.1 Сохранение углов
- •3.2.2 Круговое свойство
1 Комплексная плоскость
1.1Комплексные числа
Действительные числа обладают существенным недостатком: не все алгебраические уравнения имеют корни, например, простейшее квадратное уравнение x2+ x+ 1 = 0 не имеет действительных корней. А подобные уравнения возникают во многих естественнонаучных задачах. Поэтому возникла потребность «расширения» множества действительных чисел, то есть создания чисел, которые включают в себя все действительные как частный случай.
Действительные числа можно интерпретировать как точки прямой. Рассмотрим теперь плоскость с выбранной декартовой системой координат xOy. Точки этой плоскости будем называть «комплексными числами». Для того, чтобы такое название было правомерным, надо уметь складывать и умножать эти числа; должны существовать нейтральные по сложению и умножению элементы (то есть 0 и 1); для каждого числа z должно существовать ему противоположное (то есть такое z', что z+ z' = 0 ) и для каждого ненулевого z — ему обратное (то есть такое z'', что z z ' ' = 1 ); кроме того, должны выполняться законы арифметики (коммутативность, ассоциативность, дистрибутивность).
Каждой точке z этой плоскости сопоставим вектор, начинающий в O и оканчивающейся в z - «радиус-вектор».
Ось абсцисс будем считать действительной прямой, то есть её точки — суть действительные числа.
О п р е д е л е н и е 1. Суммой двух чисел z1 и |
z2 |
называется такое число z , радиус- |
|
вектор которого есть сумма радиус-векторов чисел |
z1 |
и z2 . |
|
Очевидно, так определённое сложение ассоциативно и коммутативно (в силу |
|||
ассоциативности и коммутативности сложения векторов). |
|||
Роль нуля играет точка O (её часто будем обозначать через 0), радиус-вектор которой есть |
|||
нулевой вектор |
0 , поэтому z+ 0 = 0+ z=z , z . |
||
|
̄ |
|
|
У т в е р ж д е н и е 1. Для каждого числа z имеется ему противоположное число u, то есть такое, что z+ u=0 .
Д о к а з а т е л ь с т в о. Число u, радиус-вектор которого имеет ту же длину, но направлен в противоположную сторону, является противоположным z в силу Определения 1.■
Число, противоположное z, будем обозначать через -z.
3
О п р е д е л е н и е 1а. Выражение z1+ (−z2) назовём разностью чисел z1 и z2 и будем обозначать через z1−z2 .
Заметим, что для точек действительной прямой введённое сложение совпадает с «обычным» сложением действительных чисел.
О п р е д е л е н и е 2. Модулем комплексного числа z (обозначается через z ) называется длина его радиус-вектора.
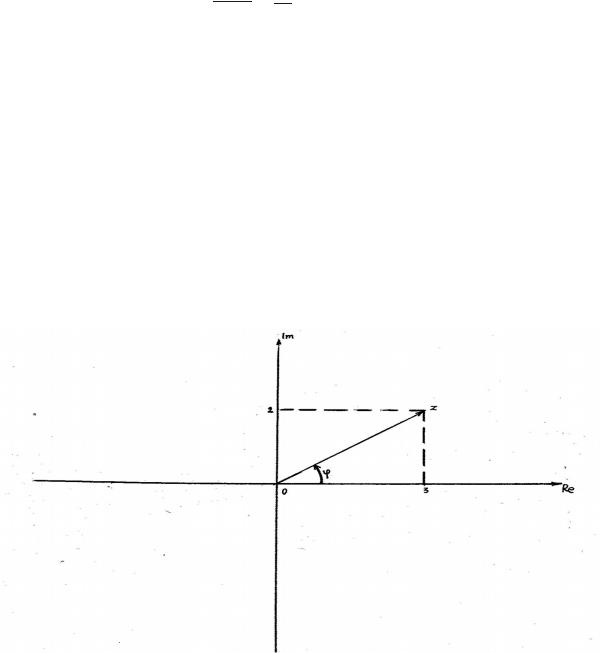
П р и м ер 1. На рис.1: z =√32 +22=√13
Заметим, что для любой точки действительной прямой так определённый модуль совпадает с «обычным» модулем действительного числа.
О п р е д е л е н и е 3. Аргументом ненулевого комплексного числа z (обозначается через arg (z) ) называется величина угла между положительным направлением оси абсцисс и
радиус-вектором z. Угол отсчитывается против часовой стрелки. Аргумент числа 0 не определяется.
Очевидно, аргумент принимает значения в промежутке [0, 2 π) . П р и м е р 2. На рис. 1 аргумент z есть φ=arctg 23 .
Аргумент действительного положительного числа равен, очевидно, 0, а отрицательного -
π .
Рис. 1. Радиус-вектор и аргумент комплексного числа.
4
У т в е р ж д е н и е 2. Справедливо соотношение |
||
arg (z)+ π , |
при |
0 arg (z)< π ; |
arg (−z)={arg (z)−π , |
при |
π arg (z )< 2 π . |
Д о к а з а т е л ь с т в о. Радиус-вектор числа -z противонаправлен радиусу-вектору числа z.
Следовательно, если 0 arg ( z)< π , то |
|
arg (−z)=arg (z )+ π |
. Если же |
π arg( z)< 2 π , |
|||||||||||
то |
arg (−z)=arg (z)−π |
|
.■ |
|
|
|
|
|
|
|
|
|
|||
Каждое комплексное число однозначно определяется модулем и аргументом. |
|
||||||||||||||
О п р е д е л е н и е 4. Произведением двух комплексных чисел |
|
z1 и |
z2 |
называется |
|||||||||||
такое число z, аргумент которого равен сумме аргументов сомножителей: |
|
|
|
||||||||||||
arg (z )=arg (z1 )+arg ( z2) , а модуль — произведению модулей сомножителей: |
|||||||||||||||
z = z1 z2 |
. Если при этом сумма аргументов получается большей или равной 2 π , то из |
||||||||||||||
неё надо вычесть 2 π . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
П р и м е р 3. На рис.2: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
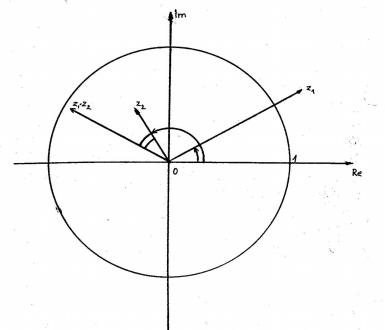
z |
>1, |
z |
<1, 0<arg (z |
1 |
)< |
π |
π <arg (z |
2 |
)<π , |
z z <1, arg ( z |
)+arg (z |
2 |
)<π . |
||
|
|||||||||||||||
|
1 |
2 |
2, |
2 |
|
1 2 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 2. Умножение комплексных чисел.
Так определённое умножение ассоциативно и коммутативно (в силу ассоциативности и коммутативности сложения и умножения действительных чисел). Роль единицы играет точка
5
действительной оси, соответствующая действительному числу 1: аргумент равен 0, а модуль равен 1.
У т в е р ж д е н и е 3. Для любого ненулевого числа z существует число u, ему обратное, то есть такое, что z u=1 .
Д о к а з а т е л ь с т в о. Рассмотрим число u такое, что модуль u равен |
1 |
, аргумент u |
|||
|
z |
||||
равен 2 π−arg(z) (если arg (z)=0 , то |
arg (u)=0 ). Тогда, в силу Определения 4, |
||||
z u=1 . ■ |
|
|
|
|
|
Число, обратное z, будем обозначать через |
1 |
или z−1 . |
|
|
|
|
z |
|
|
|
|
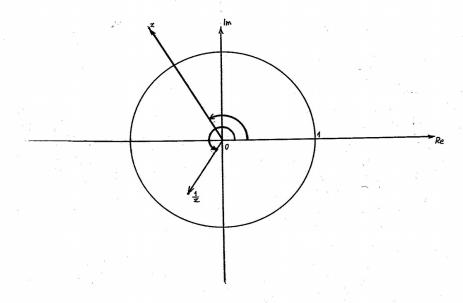
П р и м е р 4. На рис. 3 изображены число z и ему обратное.
Рис. 3. Обратное число. |
|
|
|
|
|
|
||||||||
О п р е д е л е н и е 4а. Выражение |
z1 |
1 |
, z2≠0 назовём частным от деления (или |
|||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
отношением) чисел z1 и z2 |
и будем обозначать через |
z1 |
. |
|||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
З а м е ч а н и е 1. Из определения отношения следует, что |
|
|
||||||||||||
|
z1 |
|
= |
z1 |
, |
arg |
z1 |
=arg z1 −arg z2 |
|
, причём если в последнем соотношении получается |
||||
z2 |
z2 |
z2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
отрицательно число, к нему надо прибавить 2 π .
6

Введённая операция умножения в случае действительных чисел совпадает с «обычным» умножением действительных чисел (очевидно).
Имеет место дистрибутивность умножения относительно сложения: для любых комплексных чисел u, v, w справедливо: u (v+ w)=u v+ u w . Это следует из подобия параллелограммов, построенных на радиус-векторах v и w, uv и uw; подробное доказательство опускаем.
Таким образом, мы построили новое множество чисел, которые можно складывать и умножать, причём все обычные свойства арифметических операций сохраняются; кроме того, это множество содержит в качестве подмножества все действительные числа, а новые операции сложения и умножения совпадают на подмножестве действительных чисел с привычными сложением и умножением.
Но комплексные числа обладают и непривычными свойствами. Обозначим через i число, модуль которого равен 1, а аргумент равен π/ 2 . Квадрат этого числа, то есть i i , равен числу, модуль которого равен 1 1=1 , а аргумент равен π/ 2+ π/2=π ; это число есть -1. Таким образом, i2=−1 , то есть из -1 можно извлечь квадратный корень! Отсюда следует, что из любого отрицательного действительного числа −a , a> 0 можно извлечь квадратный корень: (√a i)2=−a (и таких корней будет два: √a i и −√a i ).
Оп р е д е л е н и е 5. Число i называется мнимой единицей.
Оп р е де л е н и е 6. Ненулевые числа, расположенные на мнимой оси называются чисто мнимыми.
Каждое чисто мнимое число можно представить в виде b i , где b — ненулевое действительное число. Например, 2i ; −11,4 i ; π2 i . Знак умножения « » при этом обычно опускают.
О п р е д е л е н и е 7. Плоскость, на которой расположены комплексные числа называют
комплексной плоскостью и обозначают , ось абсцисс называют действительной осью и
обозначают R e (от французского réel), ось ординат — мнимой осью и обозначают I m (от французского imaginaire).
У т в е р ж д е н и е 4. Аргумент чисто мнимого числа, расположенного в верхней полуплоскости, равен π/ 2 , расположенного в нижней полуплоскости, равен 3 π/2 . Д о к а з а т е л ь с т в о. Следует непосредственно из Определения 3.■
Рассмотрим произвольное ненулевое комплексное число z. Разложим его радиус-вектор r по осям: r =u+ v . Проекция на действительную ось u есть радиус-вектор некоторого
7
действительного числа a, а проекция на мнимую ось v есть радиус-вектор некоторого чисто мнимого числа b i .
О п р е де л е н и е 8. Число a называется действительной частью z, Число b называется называется мнимой частью z.
Комплексное число z с действительной частью a и мнимой частью b можно записать так: z=(a ,b) . Это есть просто запись точки z (или соответствующего её радиус-вектора) в
выбранных координатах. |
|
|
||
Любое действительное число x записывается в виде |
(x ,0) , любое чисто мнимое число yi |
|||
записывается как (0, y) . |
|
|
||
У т в е р ж д е н и е 5. Пусть z=(a ,b) , тогда |
|
|||
|
|
arctg b , при a> 0, b 0 ; |
|
|
|
|
a |
|
|
z =√ |
|
; arg (z )= 2 π+ arctg b |
|
|
a2+ b2 |
, при a> 0, b< 0 ; |
|||
|
|
a |
|
|
|
|
b |
|
|
|
|
{π+ arctg a , |
при a< 0 |
. |
Д о к а з а т е л ь с т в о. Первое соотношение следует из теоремы Пифагора, второе — из
определения арктангенса.■ |
|
|
|
|
О п р е д е л е н и е 9. Сопряжённым к комплексному числу z (обозначается через |
z |
) |
||
|
|
|
̄ |
|
называется число, действительная часть которого та же самая, а мнимая имеет |
|
|
||
противоположный знак: если |
z=(a ,b) , то |
z=(a ,−b) . |
|
|
|
|
̄ |
|
|
8
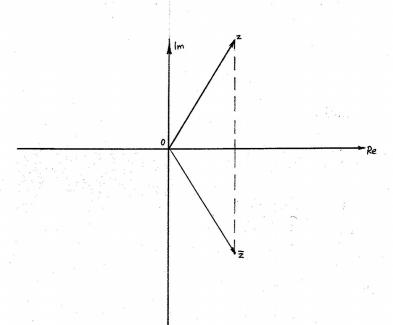
Рис. 4. Комплексное сопряжение. |
|
|
У т в е р ж д е н и е 6. |
arg (z )=2 π−arg ( z ); z = z . |
|
|
̄ |
̄ |
Д о к а з а т е л ь с т в о. Первое соотношение следует из того, что точка, соответствующая ̄z , симметрична точке, соответствующей z относительно действительной оси. Второе
соотношение сразу следует из Утверждения 5.■ У т в е р ж д е н и е 7. ̄z z= z 2
Д о к а з а т е л ь с т в о. Немедленно следует из Утверждения 6. ■ З а д а ч а 1. Доказать, что
(а) |
x= x , x |
; |
|
|
|
|
̄ |
|
|
|
|
(б) |
z= z . |
|
|
|
|
|
̄ |
|
|
|
|
Р е ш е н и е. |
|
|
|
|
|
(а) |
x x=(x ,0) x=(x ,−0)=x |
; |
|||
|
|
|
̄ |
|
|
(б) |
z=(a ,b) ̄z=( |
|
)=(a ,b)=z |
. ■ |
|
a ,−b |
|||||
Из Определения 1 следует, что координаты суммы двух комплексных чисел суть суммы
соответствующих координат: |
(x1 ; y1)+ (x2 ; y2 )=( x1+ x2 ; y1+ y2 ) . |
|
|
|
|
|
|
|
||||||||||||||||||
П р и м е р 5. |
(−3 ;2)+ (5 ;9)=(2 ;11) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Координаты произведения двух чисел записываются сложнее. Заметим сперва, что |
|
|
||||||||||||||||||||||||
(u ,v ) ( x ,0)=(u x ,v x) |
. Это следует из того, что |
(x ,0) = x |
, |
arg (x ,0)=0 |
при |
|
x> 0 |
|||||||||||||||||||
и |
arg (x ,0)=π |
при |
x< 0 |
. Далее, |
(u , v ) (0, y )=(−v y , u y) |
. Это следует из того, что |
||||||||||||||||||||
(0, y) = y , |
arg (0, y )=π/2 |
при |
y> 0 |
|
и |
arg (0, y )=3/ 2 π |
при |
y< 0 |
|
, а при |
||||||||||||||||
повороте на угол |
π/2 |
против часовой стрелке вектор с координатами |
(a ,b) |
|
|
|
|
|||||||||||||||||||
превращается в вектор с координатами |
(−b , a) |
. Воспользуемся теперь |
|
|
|
|
|
|
|
|||||||||||||||||
дистрибутивностью умножения относительно сложения: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(u ,v ) ( x , y)=(u ,v ) ((x ,0)+ (0, y))=(u ,v ) ( x ,0)+ (u , v) (0, y)=(u x ,v x)+ (−vy ,u y)= . |
||||||||||||||||||||||||||
=(ux−vy , vx+ uy ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
П р и м е р 6. |
(−3 ;2) (5 ; 9)=(−15−18 ;10−27)=(−33 ;−17) . |
|
|
|
|
|
|
|
|
|||||||||||||||||
Выведем формулу частного двух комплексных чисел. Именно, пусть |
|
|
|
|
|
|
|
|||||||||||||||||||
z1=(x1 , y1 ), |
z2=(x2 , y2)≠(0,0) |
. Так как |
|
z1 |
=z1 z2−1 , то задача сводится к нахождению |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
z |
|
|
|
|
|
|
z |
|
|
||
−1 |
|
|
|
|
|
|
z z = z |
z |
|
̄2 |
=1 |
|
|
z |
−1= |
̄2 |
|
|
||||||||
. Из Утверждения 7 следует, что |
2 |
|
|
, то есть |
z |
2 . |
||||||||||||||||||||
z2 |
|
2 |
̄2 |
2 |
|
z |
2 |
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|||||
9
|
|
z |
1 |
|
z z |
|
=( |
x x |
+ y |
1 |
y |
2 |
|
−x |
1 |
y |
+ y |
1 |
x |
2 |
) . |
|||||||
Следовательно, |
|
|
= |
1 ̄2 |
|
1 2 |
|
|
|
|
, |
|
|
2 |
|
|
|
|||||||||||
|
z |
2 |
z2 2 |
|
x22+ y |
22 |
|
|
x22 + y22 |
|
|
|||||||||||||||||
|
(−3 ;2) |
=( |
−15+ 18 |
27+ |
10 |
)=( |
|
3 |
|
|
37 |
) . |
||||||||||||||||
П р и м е р 7. |
|
|
|
; |
|
|
|
; |
|
|||||||||||||||||||
(5 ;9) |
25+ 81 |
|
25+ |
81 |
106 |
106 |
||||||||||||||||||||||
Пользоваться этими формулами умножения и деления неудобно. Более удобный способ умножать и делить комплексные числа состоит в следующем. Любое комплексное число
z=(a ;b) можно представить в виде суммы z=(a ;0)+ (0 ;b) . Первое слагаемое есть действительное число a, второе — чисто мнимое число bi (см. Определение 6). Поэтому для краткости число z записывают так: z=a+ bi . Иногда, для удобства, мы будем писать также z=a+ ib .
Для записанных в таком виде комплексных чисел не надо запоминать формулу умножения;
два числа |
|
u1+ v1 i , u2+ v2 i |
умножаются «как обычно», учитывая только тот факт, что |
||||||||||
i2=−1 |
: (u1+ v1 i) (u2+ v2 i)=u1 u2 + v1 u2 i+ u1 v2 i+ v1 v2 i2=u1 u2−v1 v2+ (u1 v2+ u2 v1)i . |
||||||||||||
Формула для частного двух комплексных чисел будет выглядеть так: |
|||||||||||||
|
x1+ y1 i |
|
= |
x1 x2 + y1 y2 |
+ |
−x1 y2+ y1 x2 |
i . |
|
|
||||
|
x2+ y2 i |
|
|
2 |
2 |
2 |
2 |
|
|
||||
|
|
|
|
x2 |
+ y2 |
|
x2 |
+ y2 |
|
|
|
||
П р и м е р 8. |
(2+ 3i)(−1+ i)=−2−3+ (2−3)i=−5−i |
; |
|||||||||||
2+ 3 i = |
1 |
|
((2+ 3i)(−1−i))= |
1 (−2+ 3+ (−3−2)i)= |
1 |
− 5 i . |
|||||||
1+ 1 |
2 |
||||||||||||
−1+ i |
|
|
|
|
2 |
|
2 |
||||||
Часто бывает удобно выразить действительную и мнимую части числа z=a+bi через его модуль и аргумент.
Из геометрических соображений очевидно, что a= z cos (arg z ), b= z sin (arg z ) . Обозначая для краткости ρ= z , φ=arg z , получим так называемую тригонометрическую форму
числа z: |
z= ρ cos φ+( ρsin φ)i= ρ(cos φ+isin φ) . Такая форма очень удобна для умножения |
||||
и деления комплексных чисел. Пусть |
|
|
|||
|
z1= ρ1 (cos φ1 + isin φ1), z 2= ρ2 (cos φ2+ i sin φ2) , |
||||
тогда (см. Определение 4 и Определение 4а) |
|
|
|||
z1 z2= ρ1 |
ρ2 (cos(φ1 + φ2 )+ i sin(φ1+ φ2)); |
z1 |
= |
ρ1 |
(cos(φ1−φ2 )+ i sin(φ1−φ2 )) , |
|
|
||||
|
|
z2 |
ρ2 |
||
последнее соотношение имеет смысл, конечно, только при z2 ≠0 .
10
П р и м е р 9.
(1+ √ 3 i) (3 1√ 2 + 31√ 2 i)=√ 1+ 3(cos π3 + i sin π3 ) √181 + 181 (cos π4 + isin π4 )=
1. |
|
|
|
|
|
|
=32 (cos(3π + 4π )+ i sin(3π + 4π ))=32 (cos 127 π + i sin 127 π ) |
|
|
|
|
|
. |
|
|
|||||||||||||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
(cos π+ i sin |
π |
) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1+ √ 3i |
|
|
|
3 |
|
π |
|
π |
|
π |
|
π |
|
|||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
3 |
|
=2 3 (cos ( π − π )+ i sin ( |
− |
))=6(cos |
+ i sin |
) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
+ |
|
|
1 |
|
i |
|
|
1 |
+ |
1 |
(cos π+ i sin π ) |
3 4 |
3 4 |
|
12 |
|
12 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3 |
|
2 |
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
√ |
|
√ |
|
|
√18 |
18 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
З а д а ч а 2. Доказать, что
(а)z1+ z2=z̄1+ z̄2 ;
(б) |
z z |
=z z |
; |
|||
|
1 2 |
̄1 |
̄2 |
|||
|
|
|
|
|
|
|
(в) |
(1z ) |
=̄1z . |
|
|
||
Р е ш е н и е.
(а) пусть z j =a j+ b j i , j=1 ; 2 , тогда
z1+ z2=a1+ a2+ (b1+ b2)i=a1+ a2−(b1+ b2)i=a1 −b1 i+ a2−b2 i=z̄1+ z̄2 ;
(б) пусть , z j = ρ j (cos φ j + i sin φ j ), j=1 ; 2 тогда
z1 z2 = ρ1 ρ2 (cos (φ1+ φ2)+ isin (φ1+ φ2)) = ρ1 ρ2 (cos(φ1+ φ2)−isin (φ1+ φ2)) =
=ρ1 ρ2 (cos(−φ1−φ2)+ i sin (−φ1 −φ2)) = ρ1 (cos (−φ1)+ isin (−φ1)) ρ2 (cos (−φ2)+ isin (−φ2)) =
=ρ1 (cos φ1−isin φ1) ρ2 (cos φ2−i sin φ2) = z̄1 z̄2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(в) так как |
|
( z |
|
) |
(z ) |
̄ |
, то, по определению обратного элемента, |
( z ) |
|
̄z |
.■ |
|||
̄ |
|
1 |
z |
= |
1 |
z |
1 |
= |
1 |
|||||
|
1=1= |
|
|
|
|
|
|
|
||||||
З а м е ч а н и е 2. При умножении числа z на число u радиус-вектор z поворачивается против часовой стрелки на угол arg u и растягивается в u раз. При делении числа z на число u радиус-вектор z поворачивается по часовой стрелке на угол arg u и сокращается в
u раз. В частности, если u =1 , то умножение или деление на u равносильно повороту в ту или иную сторону на arg u .
11
П р и м е р 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. Чтобы умножить некоторое число на i, надо повернуть его радиус-вектор на |
π/ 2 против |
||||||||||||||||||||||||||||||||||||
часовой стрелки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Чтобы разделить какое-либо число на |
|
|
|
1 |
|
+ |
|
1 |
|
i , надо повернуть его радиус-вектор |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
√ 2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
на |
π/ 4 |
по часовой стрелке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
З а д а ч а |
3. |
Доказать, что |
(cos φ+ i sin φ)n =cos nφ+ i sin nφ , |
n . |
|
|
|
||||||||||||||||||||||||||||||
Р е ш е н и е. Обозначим |
|
z=cos φ+ i sin φ . Так как |
|
z =√ |
|
|
=1, |
|
, то |
||||||||||||||||||||||||||||
|
|
cos2 φ+ sin2 φ |
arg (z)=φ |
||||||||||||||||||||||||||||||||||
z n =1, |
arg (zn )=nφ |
. Последнее равенство следует понимать как равенство с точностью до |
|||||||||||||||||||||||||||||||||||
слагаемого |
2 π k |
(то есть найдётся такое целое k, что этот аргумент равен |
nφ+ 2 π k |
). Но |
|||||||||||||||||||||||||||||||||
у числа |
cos nφ+ i sin nφ |
модуль равен 1, а аргумент равен |
nφ |
(с точностью до |
|
||||||||||||||||||||||||||||||||
слагаемого |
2 π k |
).■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С л е д с т в и е (формула Муавра) |
zn= z n(cos nφ+ isin nφ), |
n . |
|
|
|
||||||||||||||||||||||||||||||||
О п р е д е л е н и е 10. |
|
(a +bi)0 = 1, (a +bi)−n =((a +bi)−1)n , |
a+bi≠0, |
n . |
|
||||||||||||||||||||||||||||||||
Корни из 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим уравнение |
|
zn =1, n . Из предыдущей задачи следует, что, например, число |
|||||||||||||||||||||||||||||||||||
ζ1=cos |
2 π |
+ i sin |
2 π |
|
будет корнем этого уравнения: |
|
ζ1n=cos |
2 π n |
+ i sin |
2 π n |
=1+ 0i=1 . |
||||||||||||||||||||||||||
|
n |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
||||||
Также и любое число вида |
ζk =cos |
2 πk |
+ i sin |
|
2 π k |
|
, |
|
k {0,1,2 , ... ,n−1} является корнем |
||||||||||||||||||||||||||||
n |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
этого уравнения: |
ζk n=cos |
2 π kn |
+ i sin |
2 π kn |
=1+ 0 i=1 . Других корней нет, поскольку |
|
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
модуль корня должен быть равен 1, а аргумент удовлетворять соотношению |
|
|
|
||||||||||||||||||||||||||||||||||
nφ=2 π k , k =0,1 ,2 , ... |
. Существует ровно n различных углов |
φ [ 0 ; 2 π) |
, |
|
|
||||||||||||||||||||||||||||||||
удовлетворяющих такому соотношению: |
|
2 πk |
|
, k {0,1 ,2 , ... ,n−1 } . |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Построим на комплексной плоскости единичную окружность с центром в точке O. Корни n-й степени из 1 располагаются в вершинах правильного n-угольника, вписанного в эту окружность так, что одна из его вершин находится в точке 1.
Пусть имеется комплексное число u=ρ(cos φ+ i sin φ) , рассмотрим уравнение
12

|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 πk |
|
|
|
|
|
|
|
2 π k |
|
|
|
|
|
|
|
|
|
|
||||
z |
|
=u , n . Очевидно, каждое число |
|
|
ζk =√ ρ(cos |
|
n |
|
+ isin |
n |
|
), k {0,1 ,... ,n−1} |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
будет корнем этого уравнения, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
n |
|
n |
|
|
|
n |
|
|
cos |
(φ+ 2 π k )n |
+ i sin |
(φ+ 2 π k )n |
|
|
=ρ(cos φ+ i sin φ) . Других корней нет, поскольку |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ζk |
|
=√ |
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
( |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
модуль корня должен быть равен |
|
|
n |
, а аргумент удовлетворять соотношению |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
√ ρ |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nψ =φ+ 2 π k , k=0,1,2 , ... |
|
. Существует ровно n различных углов |
ψ [ 0 ; 2 π) |
, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
удовлетворяющих такому соотношению: |
|
φ , |
φ+ 2 π 1 |
, |
φ+ 2 π 2 , ... |
, |
φ+ 2 π (n−1) . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
||||||||||
С л е д с т в и е. Уравнение |
|
x2+ a=0, a> 0 |
|
|
|
имеет ровно два чисто мнимых корня: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x1=√ |
|
|
i , x2=−√ |
|
i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
С л е д с т в и е. Уравнение |
|
ax2+ bx+ c=0, a≠0 |
|
имеет ровно два (возможно, кратных) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
корня: |
|
|
|
|
x1= |
1 |
(−b+ √ |
|
), |
x2= |
1 |
|
|
(−b−√ |
|
|
), D=b2−4 ac |
|
|
, где, в случае |
D< 0 |
, |
√ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
D |
|
D |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
D |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
есть |
|
|
i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
√ D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
П р и м е р 10. Решить уравнение |
|
|
2 x2 +3 x +5=0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
i)=− 3 + |
|
√ |
|
|
|
|
x2=− |
3 |
− |
√ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Р е ш е н и е. |
|
|
|
D=32−4 2 5=−31, x1 = |
(−3+ √ |
|
|
31 |
i , |
31 |
|
i |
.■ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
31 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
||||||||
З а м е ч а н и е 3. Если уравнение |
|
|
a0 xn+ a1 xn−1+ ...+ an−1 x+ an=0 |
|
с действительными |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
коэффициентами a0 xn+ a1 xn−1+ ...+ an−1 x+ an=0 |
имеет корень |
z=u+ iv |
с ненулевой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
мнимой частью, то оно имеет и корень |
|
z=u−iv |
. Это следует из цепочки равенств |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
+ a1 z |
n−1 |
+ |
...+ an−1 z+ an = a |
|
|
n |
+ a1 z |
n−1 |
+ |
...+ an−1 z+ an = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
0 = 0 |
|
= a0 z |
|
|
0 z |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= a |
0 |
|
z n+ a |
|
zn−1+ ...+ a |
n−1 |
z + a |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
̄ |
|
|
|
|
1 ̄ |
|
|
|
|
|
|
̄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Так же, как и в случае действительных чисел, рассматриваются последовательности |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
комплексных чисел |
|
z |
|
|
, z |
|
, ... , z |
|
, ... |
. Например, |
{1 |
+ |
|
i |
} , |
|
|
{cos n+isin n } . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
З а м е ч а н и е 4. Часто бывает удобно нумеровать члены последовательности с помощью целых неотрицательных чисел (то есть начинать не с 1, а с 0).
Аналогичным образом вводится понятие предела последовательности.
13
О п р е д е л е н и е 11. Число |
z |
называется пределом последовательности |
||||
z1 , z2 , ... , zn , ... (обозначается z=lim zn ), если для всякого |
ε >0 найдётся такое |
|||||
|
|
n →∞ |
|
|
|
|
натуральное N, что для любого |
n> N |
справедливо |
z |
−z <ε |
. Также говорят, что |
|
n |
|
|||||
последовательность z1 , z2 , ... , zn , ... |
сходится к z. |
|
|
|
|
|
ти. |
|
|
|
|
|
|
О п р е д е л е н и е 11а. Говорят, что пределом последовательности |
z1 , z2 , ... , zn , ... |
|||||
является ∞ (обозначается |
lim zn=∞ ), если для всякого R>0 |
найдётся такое |
||||
|
n→∞ |
|
|
|
|
|
натуральное N, что для любого |
n> N |
справедливо |
z |
>R . |
|
|
|
|
n |
|
|
||
Так же, как и в случае действительных чисел, справедливо следующее утверждение.
У т в е р ж д е н и е 8. Если у последовательностей |
{un }, {vn } существуют конечные |
|||||||
пределы u и v соответственно, то у последовательностей |
{cun }, c , {un+vn }, {un vn } |
|||||||
также существуют пределы, равные c u , u+v , u v |
|
соответственно. Если при этом |
||||||
|
|
|
|
|
un |
|
u |
|
v≠0 , то существует предел последовательности |
{ |
|
} |
, равный |
v |
|||
vn |
||||||||
|
{vn } |
|
|
|
|
|
|
|
(последовательность |
|
un |
может быть определена начиная с некоторого n0 ). |
|||||
|
|
|||||||
Так же, как и в случае действительных чисел, рассматриваются ряды комплексных чисел
∞
∑ z j . Аналогичным образом вводится понятие суммы ряда.
j=1
|
|
|
|
|
∞ |
О п р е д е л е н и е 12. Число |
S |
называется суммой ряда ∑ z j (обозначается |
|||
|
|
|
|
|
j=1 |
∞ |
|
|
|
|
|
S = ∑ z j ), если |
S = lim Sn |
, где |
{S n } |
есть последовательность частичных сумм |
|
j=1 |
n →∞ |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
S n = ∑ z j . |
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
∞ |
∞ |
|
|
|
|
∑ u j , ∑ v j |
сходятся к u и v соответственно, то ряды |
||
У т в е р ж д е н и е 9. Если ряды j=1 |
j =1 |
|
|||
14
∞ |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
∑ cu j , c |
и |
∑ u j + v j |
также сходятся к |
c u |
и |
u+ v |
соответственно. |
||||||
j=1 |
j=1 |
||||||||||||
|
|
|
|
∞ |
|
|
|
|
|
∞ |
|
|
|
У т в е р ж д е н и е 10. Если ряд |
∑ z j |
сходится, то ряд |
∑ z j |
также сходится. |
|||||||||
|
|
|
|
j=1 |
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
О п р е д е л е н и е 13. Если ряд |
∑ z j |
сходится, то ряд |
∑ z j |
называется абсолютно |
|||||||||
|
|
|
|
j=1 |
|
|
|
|
|
j=1 |
|
|
|
сходящимся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
|
|
Степенной ряд |
a0 +∑ a j z j |
будем обозначать через |
∑ a j z j . |
|
|
||||||||
|
|
j=1 |
|
|
|
|
|
|
j=0 |
|
|
|
|
|
|
|
∞ |
(bi) |
j |
|
|
|
|
|
|
|
|
У т в е р ж д е н и е 11. Ряд |
∑ |
|
сходится к |
cos b+isin b |
для всех b . |
||||||||
|
|
|
j=0 |
j ! |
|
|
|
|
|
|
|
|
|
О п р е д е л е н и е 14. Экспонента комплексного числа |
a+ bi |
(записывается как ea+bi ) |
|||||||||||
есть ea (cos b+ i sin b) .
С л е д с т в и е. eπi = −1 .
С л е д с т в и е. Любое (ненулевое) комплексное число z можно представить в виде z= z ei arg z (показательная форма записи комплексного числа).
О с н о в н а я т е о р е м а а л г е б р ы.
Любой многочлен n-й степени с комплексными коэффициентами имеет хотя бы один корень. Б е з д о к а з а т е л ь с т в а.
З а м е ч а н и е 5. В частном случае, когда коэффициенты действительны, многочлен также имеет хотя бы один корень, мнимая часть которого может быть ненулевой. Например, одним
из корней многочлена x4+ 1 |
является |
1 |
|
+ |
1 |
|
i |
. |
||
|
|
|
|
|
|
|
|
|
||
|
|
√2 |
√2 |
|
||||||
|
|
|
|
|
||||||
С л е д с т в и е. Любой многочлен n-й степени с комплексными коэффициентами имеет ровно n корней (считая с кратностями).
Д о к а з а т е л ь с т в о. Имеется многочлен n-й степени
pn (x)=a0 xn+ a1 xn−1+ ...+ an−1 x+ an с комплексными коэффициентами.
Из основной теоремы алгебры следует, что имеется хотя бы один корень x0 . Разделим с
остатком pn (x) на |
(x−x0) |
: |
|
|
|
pn (x)=q(x )(x−x0)+ r(x) |
, |
(*) |
|
где степень многочлена r(x ) |
меньше 1, то есть |
r(x )=C |
- число. Но при подстановке |
|
x0 в (*) получаем |
0=0+ C |
(так как x0 - корень) . Следовательно, |
||
15

|
pn (x)=q(x )(x−x0) |
. Степень многочлена |
|
|
q( x) |
равна |
n−1 |
; |
q( x) , в силу основной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
теоремы алгебры, имеет корень |
x1 |
. Применяя те же рассуждения к |
|
q( x) |
, получим |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
q( x)=s( x)(x−x1), |
pn (x)=s (x)(x−x1 )( x−x0) |
, степень |
|
s(x) |
равна |
|
|
n−2 |
. И так далее. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В результате находим, что многочлен |
|
pn (x) |
имеет n корней (среди которых, возможно, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
есть совпадающие).■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
П р и м е р 11. Многочлен |
|
|
x4+ 1 |
имеет 4 различных корня: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
+ |
1 |
|
|
i, |
1 |
|
− |
1 |
|
|
i , − |
|
1 |
+ |
|
1 |
i , − |
1 |
− |
1 |
|
|
i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
√2 |
√2 |
|
|
√2 |
|
√2 |
|
|
|
√2 |
|
|
|
√2 |
|
√2 |
|
|
√2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
З а м е ч а н и е 6. Если у многочлена |
|
pn (x) |
с действительными коэффициентами |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
имеется корень |
|
x |
0 |
|
|
с ненулевой мнимой частью, то |
x |
|
также будет корнем |
|
pn (x) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
̄0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Д о к а з а т е л ь с т в о. Пусть |
pn (x)=a0 xn+ a1 xn−1+ ...+ an−1 x+ an , |
a j , |
j=0, ..., n |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тогда (поскольку |
|
|
̄t =t t ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
̄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
(x |
|
)=a |
|
x |
|
n |
+ a |
|
x |
n−1 |
+ ... |
+ a |
|
x |
|
+ a |
=a |
x |
n |
+ ...+ a |
|
|
x |
|
+ a |
=a |
x |
|
+ ...+ a |
|
x |
+ a , |
|||||||||||||||||||||||||||||
0=0= p |
0 |
0 |
0 |
1 |
0 |
|
|
|
0 |
|
|
n−1 |
0 |
0 |
|
n−1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
n |
|
|
|
0 0 |
|
|
|
|
|
̄n |
|
|
0 ̄ |
|
|
|
|
̄0 |
|
n |
||||||||||||||
|
|
|
|
|
|
|
x |
|
- корень |
|
|
pn (x) .■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
то есть ̄0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
16
Основные факты, необходимые для решения задач.
1.Алгебраическая форма записи комплексного числа: z=a+ bi , где i -мнимая
единица. Числа вида z=a+0 i являются действительными и записываются как a; числа вида называются чисто мнимыми и записываются как bi .
2.i2=−1 .
3. |
|
|
|
Число |
|
z= |
a+ bi |
=a−bi |
|
называется сопряжённым к |
z=a+ bi |
. |
||||||
|
|
|
|
̄ |
|
|
|
|
|
|
||||||||
4. |
|
|
|
Сложение комплексных чисел: если |
z1=a1+ b1 i , z2=a2+ b2 i |
, то |
||||||||||||
|
z1+ z2=(a1+ a2 )+ (b1+ b2)i . |
|
|
|
|
|
|
|
|
|||||||||
5. |
|
|
|
Умножение комплексных чисел: если |
z1=a1+ b1 i , z2=a2+ b2 i , то |
|||||||||||||
|
z1 z2=(a1 a2 −b1 b2 )+ (a1 b2+ a2 b1 )i . |
|
|
|
|
|
|
|||||||||||
6. |
|
|
|
Деление комплексных чисел: если |
z1=a1+ b1 i , z2=a2+ b2 i |
, то |
|
|||||||||||
|
z1 |
= |
|
a1 a2+ b1 b2 |
+ |
−a1 b2+ a2 b1 |
i |
. |
|
|
|
|
|
|
||||
|
z2 |
|
a22+ b22 |
|
a22+ b22 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7. |
|
|
|
Тригонометрическая форма записи комплексного числа: z=ρ(cos φ+ isin φ) , где |
||||||||||||||
ρ |
- модуль (записывается как |
ρ= z |
), |
φ [0 ; 2 π) |
- аргумент (записывается как |
|||||||||||||
φ=arg z ). Если |
z=a+ bi |
, то |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
arctg b , при a >0, b 0 ; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
ρ=√ |
|
; |
φ= 2 π+arctg b , |
|
|
|
|
|
||||||||||
a2 +b2 |
при a>0, b<0 ; , |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{π+arctg a , |
при a<0 |
|
|
zn=ρn(cos nφ+ isin nφ) . |
||||||
8. |
|
|
|
Формула Муавра: если |
|
z=ρ(cos φ+ isin φ) , то |
||||||||||||
9. |
|
|
|
Показательная форма записи комплексного числа: |
z=ρei φ |
, где ρ, φ - модуль и |
||||||||||||
аргумент z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
17
