
- •1 Комплексная плоскость
- •1.1 Комплексные числа
- •Задачи
- •1.2 Области, пути и кривые,
- •2 Функции комплексного переменного
- •2.1 Понятие функции
- •2.2 Предел функции
- •2.3 Непрерывность
- •2.4 Линейные функции
- •2.5 Дифференцируемость
- •2.6 Геометрическая интерпретация производной
- •3 Стереографическая проекция
- •3.1 Стереографическая проекция и бесконечность
- •3.2 Свойства стереографической проекции
- •3.2.1 Сохранение углов
- •3.2.2 Круговое свойство
отображением в комплексном смысле |
f : → , см. Замечание п.2. |
|||||||
С л е д с т в и е. Из Теоремы 2 следует, что |
|
|
|
|
|
|||
f ' (a)= ∂ u(a) +i |
∂ v (a ) |
=∂ f (a) , |
f ' (a )= |
∂ v(a) |
−i |
∂u (a ) |
= |
1 ∂ f (a) . |
∂ x |
∂ x |
∂ x |
|
∂ y |
|
∂ y |
|
i ∂ y |
Это означает, что для нахождения производной достаточно продифференцировать функцию только по x (или только по y).
О п р е д е л е н и е 4. Точка a называется стационарной точкой функции f, если f
дифференцируема в a и |
f ' (a)=0 . |
|
П р и м е р 4. |
|
|
1. У функции |
f (z)=z2 |
имеется одна стационарная точка z=0 . |
2. У функции |
f (z)=ez |
стационарных точек нет. |
З а д а ч а |
1. Найти стационарные точки функции |
f (z)=z3 +3 z . |
||
Р е ш е н и е. Так как |
f ' (z)=3 z2 +3 , то у функции f (z)=z3 +3 z имеются две |
|||
стационарные точки - |
±i |
.■ |
|
|
З а д а ч а |
2. Найти стационарные точки функции |
f (z)=ez +e−z . |
||
Р е ш е н и е. У функции |
f (z)=ez +e−z имеется бесконечно много стационарных точек - |
|||
πki , k (так как f ' ( x+iy)=∂ f (x +iy)=ex (cos y+i sin y )−e− x(cos y−i sin y) ).■
∂x
Оп р е д е л е н и е 5. Функция f называется голоморфной (или аналитической) в точке a, если она дифференцируема в некоторой окрестности этой точки.
П р и м е р 5. Все функции Примера 4 голоморфны в .
2.6Геометрическая интерпретация производной
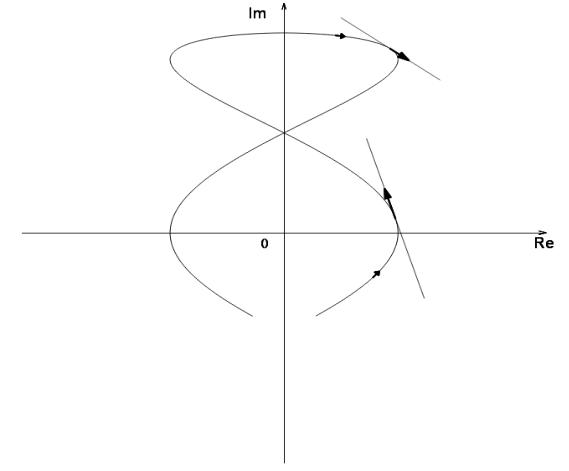
Пусть на комплексной плоскости имеется гладкая кривая γ (t)=φ(t)+iψ (t), t [ α,β] , см. Определение 9 п.1.2. На каждой касательной к этой кривой выберем один из тех направляющих векторов, которые соответствуют направлению кривой, см. рис.1.
46
|
Рис. 1. |
|
|
||
Пусть теперь имеются две гладкие кривые |
γ1 ,γ2 , пересекающиеся в точке a. Обозначим |
||||
через |
u |
, u |
направляющие вектора их касательных в точке a, соответствующие |
||
|
1 |
2 |
|
|
|
направлениям кривых. |
|
|
|||
О п р е д е л е н и е 1. Углом между кривыми |
γ1 ,γ2 в точке a называется меньший из |
||||
углов, на который надо повернуть вектор |
u |
, чтобы он стал коллинеарен и сонаправлен |
|||
|
|
|
|
1 |
|
вектору |
u |
. Если направление вращения совпадает с направлением против часовой |
|||
|
|
2 |
|
|
|
стрелки, то угол считается положительным, в противном случае — отрицательным. Если векторы параллельны и противонаправлены, то угол между ними принимается равным π . П р и м е р 1. На рис.2 угол между γ1 , γ2 в нижней точке пересечения положителен, а в верхней — отрицателен.
З а м е ч а н и е 1. Так определённый угол между кривыми зависит от порядка, в котором взяты кривые: углы между γ1 , γ2 и γ2 , γ1 равны по абсолютной величине и имеют разные знаки.
47
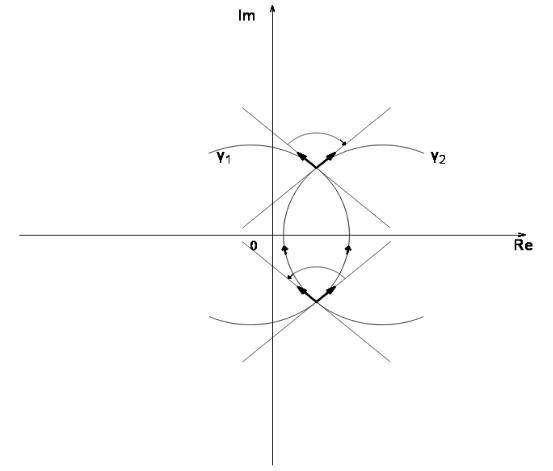
Рис. 2.
О п р е д е л е н и е 2. Если угол между кривыми в точке a равен 0 или π , то говорят, что кривые касаются в точке a.
П р и м е р 2. На рис.3 окружности касаются в точке A.
48

Рис.3.
З а д а ч а 1. Найти углы между кривыми γ1 , γ2 в точках A, B, C на рис.4(a),(b).
49
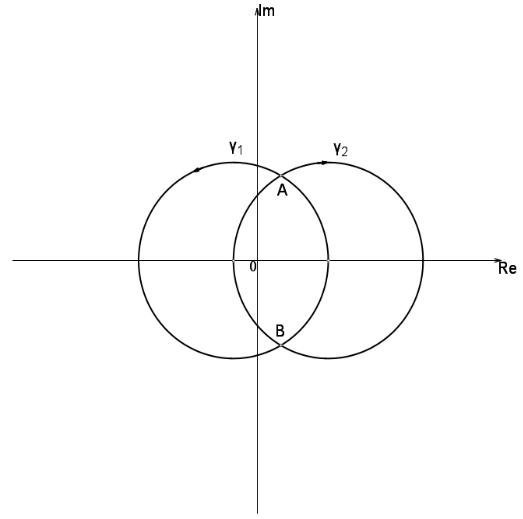
Рис.4(a). |
γ1 (t)=4 cos t−1+4 i sin t , |
|
|
γ2 (t)=4 cos t+3−4i sin t , |
t [ 0, 2 π] |
50
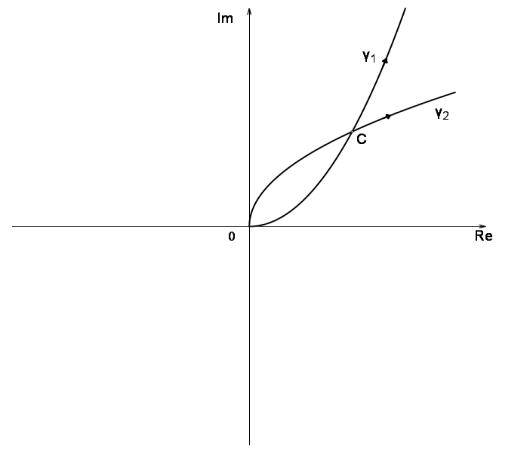
Рис.4(b). |
γ1 (t)=t+it 2 , |
γ2 (t )=t +i √ |
|
, |
t [ 0, 2 ] |
|
|
|
|
|
|
t |
|
|
|
|
|
||||||
Р е ш е н и е. (a) |
|
|
|
|
|
|
|
|
|
|
|
Угол O1 AO2 |
равен π /3 , см. рис.4(с), угол O2 AC1=O1 AC2 |
равен |
π /2 |
, поэтому |
|||||||
C1 A , C2 A |
являются касательными в точке A к γ2 ,γ1 соответственно и абсолютное |
||||||||||
значение искомого угла равно |
2 π /3 |
. Направление вращения от |
u |
к |
u |
- по часовой |
|||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
стрелке, следовательно, угол между |
γ1 , γ2 |
в точке A равен |
−2 π /3 . |
|
|
|
|||||
Те же рассуждения приводят к выводу, что угол между γ1 ,γ2 |
в точке B равен |
2 π /3 . |
|||||||||
51
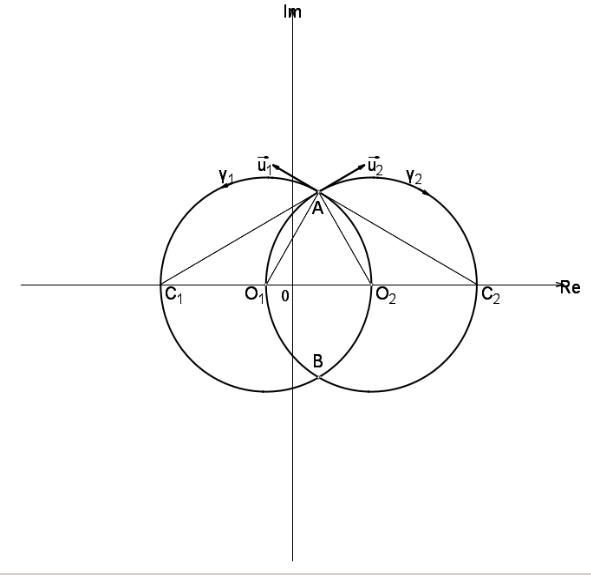
Рис.4(с).
52
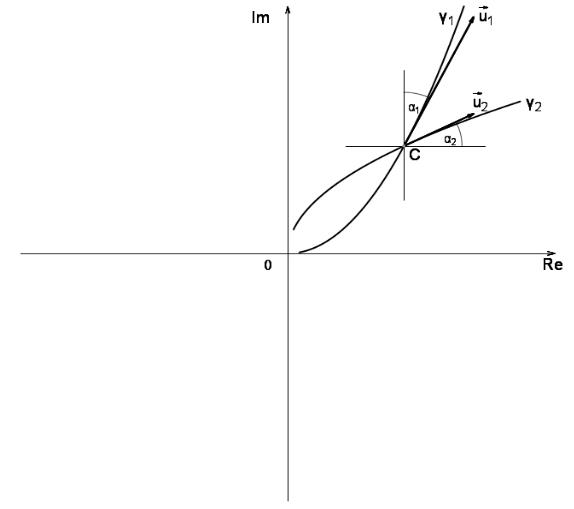
Рис.4(d).
(b) Очевидно, точка C пересечения кривых γ1 , γ2 есть 1+i . Из правила дифференцирования параметрически заданной функции следует, что угловые коэффициенты
|
|
|
(t2)' |
|
(√ |
|
)' |
|
1 |
|
|
|||
касательных к кривым |
γ1 |
, γ2 равны |
=2 t , |
t |
= |
|
соответственно, поэтому |
|||||||
t ' |
t ' |
|
|
|||||||||||
2 √t |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||
tg ( |
π |
−α1)=2 , tg α2= |
1 |
. Следовательно, |
α1=α2 =arctg |
1 |
|
и, поскольку направление |
||||||
2 |
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||
вращения от |
u |
к |
u |
- по часовой стрелке, искомый угол равен |
(2 |
2 ) |
.■ |
− π −2 arctg |
1 |
||||||
|
1 |
|
2 |
|
|
|
|
Пусть функция f(z)=u(z)+iv(z) определена в некоторой окрестности точки a, функции u, v дифференцируемы в точке a как функции двух действительных переменных (для этого
53
достаточно существования и непрерывности в некоторой окрестности точки a частных
производных |
∂u |
, |
∂ v |
, |
∂u |
, |
∂ v |
) и матрица, составленная из этих производных в точке |
|
∂ x |
∂ x |
∂ y |
∂ y |
||||||
|
|
|
|
|
a , невырождена (то есть точка a не является критической).
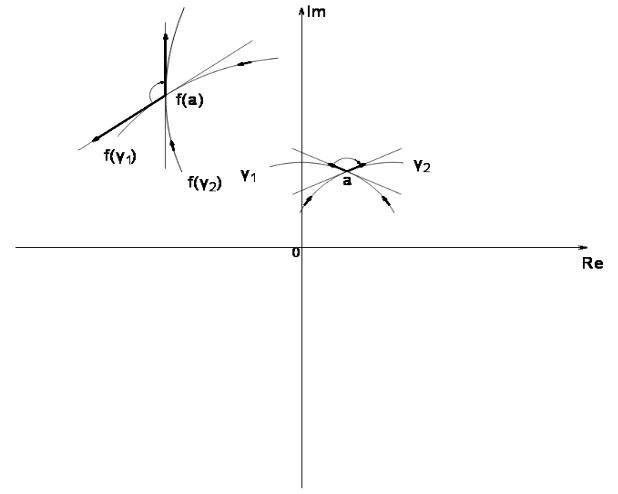
О п р е д е л е н и е 3. Такая функция f называется конформной в точке a, если угол между любыми гладкими кривыми γ1 , γ2 в точке a равен углу между их образами f (γ1),f (γ2 ) в точке f (a) , см. рис.5.
Рис.5.
Т е о р е м а 1. Если функция f является дифференцируемой в комплексном смысле в точке a и f ' (a)≠0 , то f конформна в точке a.
Д о к а за т е л ь с т в о. Как известно из действительного анализа, дифференциал (дифференцируемого в действительном смысле) отображения плоскости в себя переводит касательные к кривым в касательные к их образам. Дифференциал дифференцируемой в комплексном смысле функции сводится к растяжению с поворотом, а такое преобразование
54
сохраняет углы между ориентированными прямыми. Подробнее. Пусть f =u+iv . Как
известно из действительного анализа, при отображении |
(x, y )→(u (x, y ),v (x , y)) |
||||
действительной плоскости в себя, направляющий вектор |
(α' ,β' ) |
касательной к кривой |
|||
(α(t),β(t)) переходит в вектор |
(u 'x α'+u' y β ' , v 'x α'+v 'y β ') |
, который является |
|||
направляющим касательной к кривой (u(α(t),β(t )), v (α(t),β(t ))) |
. Из |
||||
дифференцируемости f в комплексном смысле следует |
|
|
|
|
|
(u'x α'+u' y β' , v 'x α'+v 'y β')=(u'x α'−v'x β' , v 'x α'+u'x β') . Правую часть последнего |
|||||
равенства можно переписать так: |
(u'x+iv 'x )(α'+iβ') . Что равно |
f ' ( x+iy)(α'+iβ' ) , см. |
|||
Следствие Теоремы 2. Таким образом, направляющие вектора касательных к кривым |
|||||
растягиваются и поворачиваются на один и тот же угол, равный |
arg |
f ' (x +iy) , |
|||
следовательно, углы между ними не меняются.■ |
|
|
|
|
|
П р и м е р 3. На рис.5 изображены кривые, пересекающиеся в точке |
1+2i и их образы |
||||
при отображении z→ z2 .
Т е о р е м а 2. Если функция f является конформной в точке a, то она дифференцируема в комплексном смысле в этой точке.
Д о к а з а т е л ь с т в о. Сперва вспомним тот факт, что если угол между вектором
( p1 , p2) , p1 , p2 |
и вектором (q1 ,q2) , q1 , q2 равен π /2 , то |
q1 = −t p2 , q2 = t p1 |
для некоторого действительного положительного t. |
Конформность функции f=u+iv в точке a означает, что f дифференцируема (в действительном смысле) в a , точка a — некритическая, сохраняются углы между касательными к кривым в точке a. Возьмём кривую, направляющий вектор касательной к которой (в точке a) имеет
координаты |
(s1 ,s2 ), s1 ,s2 . Возьмём также кривую, направляющий вектор касательной |
||||
к которой (в точке a) имеет координаты |
(−s2 ,s1) |
. Угол между первой и второй кривой |
|||
равен π /2 |
. Образы направляющих векторов суть |
(u ' x s1 +u ' y s2 , v 'x s1 +v' y s2 ) |
и |
||
(−u' x s2 +u' y s1 , −v' x s2 +v ' y s1) . Угол между ними должен также равняться π /2 |
, что |
||||
−(v 'x s1 +v ' y s2 ) = t(−u ' x s2 +u ' y s1) |
|
|
|
||
означает { |
u' x s1 +u' y s2 = t (−v 'x s2 +v' y s1 ) |
при некотором действительном |
|
||
положительном t. В силу произвольности |
s1 ,s2 |
получаем соотношения |
|
||
55
|
−v ' x = t u ' y |
−v' x = u ' y . |
−v' y = −t u' x , откуда (так как u'x+i v 'x≠0 ) следует t=1 и |
||
{ |
u'x = t v' y |
{ v' y = u' x |
u' y = −t v x |
|
|
Получено условие CR, что, в силу Теоремы 2 п.2.5, влечёт дифференцируемость f в точке a.■
З а д а ч а 2. Дифференцируема ли в 0 функция |
g (z)= z z ? |
Р е ш е н и е. Поскольку g(0+Δ z)−g (0)=Δ z |
z =0(Δ z)+o (Δ z) , то из определения |
дифференцируемости следует, что функция дифференцируема в 0 и её производная в 0 равна 0.■
З а д а ч а |
3. |
Сохраняет ли углы в точке 0 функция |
g(z)=z z ? |
|
Р е ш е н и е. Так как |
g (z )= ρ2(cos φ+i sin φ) , то g оставляет на месте лучи, выходящие из |
|||
0, и, следовательно, сохраняет углы между ними. ■ |
|
|||
З а д а ч а |
4. |
Сохраняет ли углы в точке 0 функция |
f (z)=z2 ? |
|
Р е ш е н и е. Так как |
f (z )= ρ2 (cos 2 φ+i sin 2 φ) |
, то f удваивает углы между лучами, |
||
исходящими из 0.■ З а м е ч а н и е 2. Таким образом, если производная функции в точке равна 0, то углы между
кривыми в этой точке могут сохраняться, а могут и не сохраняться.
56
