
- •1 Комплексная плоскость
- •1.1 Комплексные числа
- •Задачи
- •1.2 Области, пути и кривые,
- •2 Функции комплексного переменного
- •2.1 Понятие функции
- •2.2 Предел функции
- •2.3 Непрерывность
- •2.4 Линейные функции
- •2.5 Дифференцируемость
- •2.6 Геометрическая интерпретация производной
- •3 Стереографическая проекция
- •3.1 Стереографическая проекция и бесконечность
- •3.2 Свойства стереографической проекции
- •3.2.1 Сохранение углов
- •3.2.2 Круговое свойство
окрестность ∞ определяется как |
U R ∞ . Открытые и замкнутые множества в |
|
̄ |
определяются так же, как и для , см. Определения 3, 4 п.1.2.
З а м е ч а н и е 5. Одно- и многосвязные области на ̄ определяются так же, как и для
, см. Определение 13 п.1.2, только ограниченности от них уже не требуется.
3.2Свойства стереографической проекции
3.2.1Сохранение углов
Те о р е м а 1. При стереографической проекции угол между гладкими кривыми,
пересекающимися в точке A S {N } , равен углу между их образами на комплексной
плоскости |
. |
|
|
|
|
Д о к а з а т е л ь с т в о. Пусть на сфере имеются гладкие кривые |
γ1 ,γ2 |
, пересекающиеся в |
|||
точке A, см рис.1 (a). Пусть точка A лежит в северной полусфере. |
|
|
|
|
|
Их образы |
γ '1 , γ '2 при стереографической проекции пересекаются в точке A'. |
||||
Направляющие векторы касательных к в точке A обозначим через |
u |
, u |
|
. Проведём через |
|
|
|
1 |
2 |
|
|
N плоскость P, параллельную (на рис.1 (a) не показана).
1. Сперва рассмотрим случай, когда ни одна из касательных не параллельна плоскости .
Проведём плоскости |
P1 , P2 |
через N и касательные. Точки пересечения касательных с |
|||||||||||
плоскостью P обозначим через |
B1 |
и B2 , а с плоскостью |
|
- через |
B '1 |
и |
B '2 . |
||||||
Предположим также, что кривые параметризованы так, что векторы |
u |
, u |
направлены от |
||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
A к |
B1 и B2 . |
|
|
|
|
|
|
|
|
|
|
|
|
Прямые A ' B '1 и A ' B '2 |
, являющиеся пересечениями плоскостей |
P1 , P2 |
с |
, |
|||||||||
суть касательные к |
γ '1 , γ '2 |
. Этот факт принимаем без строгого доказательства; пояснить |
|||||||||||
можно следующим образом. При проецировании кривой |
γ1 |
на плоскость |
|
луч из N, |
|||||||||
проходящий через точки кривой |
γ1 |
, описывает некоторую (коническую) поверхность Π, |
|||||||||||
которая касается плоскости |
P1 |
в точке A, поскольку кривая |
γ1 |
|
касается прямой |
AB1 . |
|||||||
Луч NA принадлежит и этой поверхности, и плоскости |
P1 , то есть поверхность Π касается |
||||||||||||
P1 |
по лучу NA. Из определения стереографической проекции следует, что кривая |
γ '1 |
|||||||||||
является пересечением Π с |
. Прямая A ' B '1 , являясь пересечением |
P1 |
и , |
||||||||||
является касательной к γ '1 . |
|
|
|
|
|
|
|
|
|
|
|||
63
Образы |
u ' |
1 |
, u ' |
2 |
векторов |
u |
, u |
являются направляющими векторами прямых |
A ' B ' |
1 |
||||
|
|
|
|
|
|
1 |
2 |
|
|
|
||||
и A ' B '2 |
|
и направлены от |
B '1 |
и B '2 |
соответственно. Поэтому направление |
|
|
|||||||
вращения от |
u |
|
|
к |
u |
, если глядеть из центра сферы, совпадает с направлением |
|
|
||||||
вращения от |
1 |
|
к |
2 |
|
на плоскости |
. |
|
|
|||||
|
|
1 |
|
2 |
|
|
||||||||
|
|
|
u ' |
|
|
u ' |
|
|
|
|
|
|
|
|
Таким образом, требуется доказать, что угол B '1 A' B '2 |
равен углу B '1 AB' 2 |
(оба угла |
|
|||||||||||
считаются положительными). |
|
|
|
|
|
|
|
|
|
|
||||
Из построения следует, что |
NB1 A' B '1 , NB2 A' B '2 |
, то есть треугольник |
AB1 N |
|
|
|
||||||||
подобен треугольнику |
AB '1 A' |
, а треугольник AB2 N |
подобен треугольнику |
AB '2 A ' |
||||||||||
. Но |
B1 N =B1 A , B2 N =B2 A |
, так как являются касательными к сфере, проведёнными из |
|
|||||||||||
одной точки, поэтому |
B '1 A=B '1 A' , B '2 A=B '2 A' |
. Следовательно, треугольники |
|
|
|
|||||||||
AB '1 B ' 2 |
и A ' B '1 B '2 |
равны, откуда следует равенство углов B '1 A' B '2 |
и |
B '1 AB' 2 . |
|
|||||||||
В случае иной параметризации кривых изменится направление векторов |
u |
, u |
и |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
u' |
, u' |
, но величины углов, образуемых касательными, останутся теми же. Рассматривая |
||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
три случая изменения направления касательных векторов (изменение направления только у |
|
|||||||||||||
одного или сразу у обоих), нетрудно видеть, что направление вращения от |
u |
к |
u |
, если |
||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
глядеть из центра сферы, будет по-прежнему совпадать с направлением вращения от |
u' |
1 |
к |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u' |
на плоскости |
. |
|
|
|
|
|
|
|
|
|
|
|
|
2
Случай, когда точка A лежит в южной полусфере, рассматривается аналогично и приводит к тому же результату. В случае, когда точка A лежит на экваторе, картина упрощается, результат остаётся тем же.
64

Рис.1 (a).
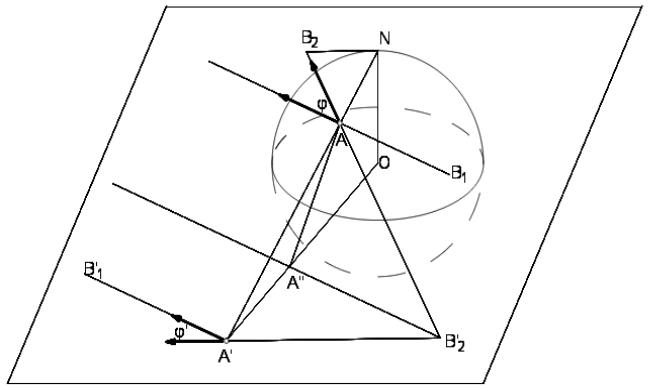
2. Пусть теперь одна из касательных параллельна плоскости , например AB1 , см. рис.1 (b). Точка пересечения другой касательной с плоскостью P по-прежнему обозначается
через |
B2 . Тогда пересечением плоскости |
P1 |
(содержащей |
AB1 |
и N) и |
|
является |
||||||
прямая |
A ' B '1 , пересечением плоскости |
P2 |
(содержащей |
AB2 |
и N) и |
|
- прямая |
||||||
A ' B '2 |
. Очевидно, AB1 A ' B '1 |
и |
NB2 A' B '2 . |
|
|
|
|
|
|||||
Плоскость, содержащая обе касательные, пересекает по прямой |
B '2 A' ' |
. Также |
|||||||||||
очевидно, что |
AB1 A ' ' B '2 . |
|
|
|
|
|
|
|
|
|
|||
Повторяя рассуждения предыдущего пункта, получаем, что надо доказать равенство |
|||||||||||||
φ=φ' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Сперва докажем, что прямая |
A B1 |
перпендикулярна плоскости AON |
. Сечение сферы |
||||||||||
плоскостью |
AB1 O является окружностью с центром в O, сечение сферы плоскостью, |
||||||||||||
проходящей через |
A B1 и перпендикулярной |
ON , является окружностью с центром, |
|||||||||||
лежащим на |
ON |
. Прямая |
A B1 |
является касательной к обеим окружностям, поэтому |
|||||||||
она перпендикулярна их радиусам, проведённым из центров в точку A. Следовательно, она |
|||||||||||||
перпендикулярна плоскости, содержащей эти радиусы, то есть |
AON . |
|
|
|
|||||||||
Отсюда следует, что прямая |
A ' ' B '2 |
также перпендикулярна плоскости |
AON . |
|
|||||||||
65
Следовательно, углы |
A ' A' ' B' 2 , |
A' A' ' A |
- прямые. |
|
|
|
||||
Треугольник AB2 N |
- равнобедренный, так как |
B2 A |
и |
B2 N |
- касательные к сфере. В |
|||||
силу подобия треугольников |
AB2 N |
и |
AB '2 A ' |
заключаем, что |
AB '2= A' B '2 . |
|||||
Следовательно, прямоугольные треугольники |
AB '2 A ' ' |
и |
A ' B '2 A' ' равны, что |
|||||||
означает и равенство углов |
AB '2 A ' ' |
и |
A ' B '2 A' ' . |
|
|
|
||||
В силу параллельности прямых |
AB1 , A' ' B '2 , A' B '1 |
отсюда следует, что φ=φ' . |
||||||||
Рис.1 (b).
Случай, когда точка A лежит в южной полусфере, рассматривается аналогично и приводит к тому же результату. В случае, когда точка A лежит на экваторе, картина упрощается, результат остаётся тем же.
3. Если обе касательные параллельны между собой, то, очевидно, угол между ними равен 0 либо ±π , и он сохраняется при стереографической проекции. ■ З а д а ч а 1. Найти абсолютное значение угла между параллелью и меридианом.
Р е ш е н и е.
При стереографической проекции углы сохраняются, следовательно, можно рассматривать углы между образами параллели и меридиана. Образ параллели — окружность с центром в точке O, образ меридиана — луч, исходящий из O. Образы пересекаются под прямым углом,
66
