поэтому абсолютная величина искомого угла равна π/2 . ■

3.2.2 Круговое свойство

Рассмотрим сперва вспомогательную конструкцию. Пусть на плоскости P имеется окружность C с центром O радиуса r. Соединим некоторую точку A, лежащую вне данной плоскости, лучами со всеми точками окружности, рис.2. Назовём полученное множество лучей наклонным круговым конусом.

Обозначим через B проекцию точки A на плоскость P.

Рис.2.

Из соображений подобия очевидно, что сечение такого конуса любой плоскостью, параллельной P, есть окружность.

У т в е р ж д е н и е 1. Плоскость AOB является плоскостью симметрии наклонного кругового конуса .

Д о к а з а т е л ь с т в о. Заметим прежде всего, что плоскость AOB ортогональна плоскости

67

P (так как содержит AB). Пусть точка K лежит на конусе. Проведём через K плоскость P', параллельную P. Сечением будет окружность C', см. рис.3. Точка K', симметричная K относительно плоскости AOB, во-первых, лежит в плоскости P', а во-вторых лежит на окружности C', то есть принадлежит конусу. ■

Рис.3.

Обозначим через AN и AM образующие конуса, лежащие в плоскости AOB, см. рис.4. Обозначим через φ угол ANM.

Обозначим через EF хорду, перпендикулярную плоскости AOB. Построим плоскость EFM', отличную от P, содержащую EF (и, следовательно, перпендикулярную к AOB) и образующую угол φ с с прямой AM, см.рис.4, 4a. В сечении получается замкнутая кривая.

68

Рис.4.

69

Рис.4a.

У т в е р ж д е н и е 2. Сечение конуса плоскостью EFM' является окружностью. Д о к а з а т е л ь с т в о.

Сперва вспомним, что точка Q лежит на окружности в том и только том случае, когда

QP2 =RP PS , где отрезок QP перпендикулярен диаметру RS,см.рис. 5. (Доказательство. Точка Q лежит на окружности тогда и только тогда, когда треугольник RPQ прямоугольный, что имеет место в том и только том случае, когда QP2 =RP PS ).

70

Также очевидно, см. рис.7, что окружность без точки N проецируется на всю прямую. Точка же N проецируется в ∞ по определению, см. п. 3.1.

О т в е т. Прямая, пополненная точкой ∞ .

Рис.6.

Т е о р е м а 1. При стереографической проекции окружности, лежащие на сфере и не проходящие через N, переходят в окружности на плоскости , а окружности на сфере, проходящие через N, - в прямые, пополненные точкой ∞ .

Д о к а з а т е л ь с т в о.

Пусть окружность проходит через N, см. также Задачу 2. Тогда плоскость, её содержащая, также содержит N и проекция окружности без точки N лежит в пересечении этой плоскости и

, то есть в прямой. Это соответствие, очевидно, взаимно-однозначное, см. рис.7.

72

Рис.7.

Точка же N проецируется в ∞ по определению, см. п. 3.1.

Пусть окружность с центром в точке O1 не проходит через N, см. рис.8. Тогда все лучи, начинающиеся в N и проходящие через окружность, образуют наклонный круговой конус, пересекающий плоскость по некоторой замкнутой кривой. Плоскость,проходящая через NO и O1 , перпендикулярна плоскости окружности (так как содержит отрезок

OO1 , перпендикулярный плоскости окружности) и является плоскостью симметрии конуса. Образующие, лежащие в пересечении конуса с этой плоскостью, обозначим через NP и NQ, а точки их пересечения с плоскостью - через P' и Q' соответственно.

Угол NQP равен половине дуги NSP. Угол PNQ равен половине дуги QP, угол P'Q'N равен половине дуги QN. Следовательно, угол NP'Q' равен половине дуги NSP, то есть угол NQP равен углу NP'Q'. В силу Утверждения 2 пересечение конуса с плоскостью является окружностью. ■

73

Рис.8.

З а м е ч а н и е 3. Центр O1 окружности на сфере не переходит в центр окружностипроекции, за исключением случая, когда плоскость окружности на сфере параллельна экваториальной.

эквивалентно повороту сферы S на угол π вокруг действительной оси.

Р е ш е н и е. Для точек O и ∞ утверждение очевидно (полюса сферы меняются местами). Если z=1 , то данное преобразование отражает единичную окружность относительно

лежит в северном полушарии, точка A' располагается в южном. Точки пересечения сферы S с AN и A'N обозначим через B и B' соответственно. Из определения стереографической проекции следует, что долгота A равна φ, долгота A' равна 2 π −φ .

Рассмотрим плоскости ANO и A'NO, см.рис.10(a),(b). Прямоугольный треугольник NOz

74

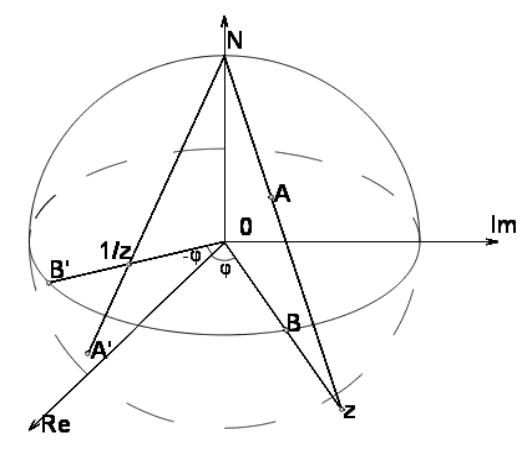
меньшему у них одинаково (и равно ρ= z ). Следовательно, угол NzO равен углу A'NO, откуда следует, что дуги AN и A'S равны. Следовательно, равны и дуги AB и A'B'.

Таким образом, точка A' получается отражением точки A относительно экваториальной плоскости и плоскости, содержащей действительную ось и N. А это означает, что она получается поворотом на угол π вокруг действительной оси.■

Рис.9.

75

Рис.10 (a).

Рис.10 (b).

Пусть γ1 ,γ2 - гладкие кривые на S, проходящие через ∞ , а Γ 1 , Γ 2 - их образы при