27. Теорема ролля Теорема Ролля

Теорема

Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Пусть функция 

1. непрерывна на отрезке ;

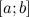2. дифференцируема на интервале ;

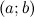3. на концах отрезка 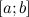принимает равные значения .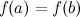

Тогда на интервале найдется, по крайней мере, одна точка , в которой .

Следствие. (Геометрический смысл теоремы Ролля)

Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.

Следствие.

Если , то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.

28. Теорема ферма Теорема Ферма

Теорема

Теорема Ферма. (О равенстве нулю производной)

Пусть функция удовлетворяет следующим условиям:

1. она дифференцируема на интервале ;

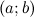2. достигает наибольшего или наименьшего значения в точке .

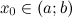Тогда производная в этой точке равна нулю, то есть .

Следствие. (Геометрический смысл теоремы Ферма)

В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.

29.Теорема коши

Теорема Коши. (Об отношении конечных приращений двух функций)

Если функции и:

1. непрерывны на отрезке ;

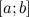2. дифференцируемы на интервале ;

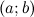3. производная 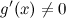на интервале,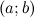

тогда на этом интервале найдется по крайней мере одна точка , такая, что

Теорема

Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.

Теорема

Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.

30. Монотонность и экстремумы функции. Применение производной. Монотонность функции, основные понятия и определения

Определение

Функция называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.

Пример

Функция является возрастающей на промежутке , так как:

для 

Определение

Функция называется строго убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.

Пример

Функция является строго убывающей на промежутке , так как:

для 

Функция строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.

Определение

Функция называется неубывающей на промежутке, если из неравенства следует неравенство .

Функция называется невозрастающей на промежутке, если из неравенства следует неравенство .

Связь монотонности функции с ее производной

Теорема

(Об условии возрастания/убывания монотонной функции)

Если производная функции на некотором промежутке , то функция возрастает на этом промежутке; если же на промежутке , то функция убывает на этом промежутке.

Замечание

Обратное утверждение формулируется несколько иначе. Если функция возрастает на промежутке, то или не существует.

Пример

Задание. Исследовать функцию на монотонность на всей числовой прямой.

Решение. Найдем производную заданной функции:

Для любого действительного : , а поэтому делаем вывод, что заданная функция возрастает на всей действительной оси.

Ответ. Функция возрастает на всей действительной оси.