Случай зависимой переменной
Пусть
задана дифференцируемая функция 
.
Тогда
где 
в
общем случае не является постоянной
величиной. Поэтому дифференциал от
функции 
берем
как дифференциал от произведения
Пример
Задание. Найти
дифференциал второго порядка 
функции 
,
где 
и 
-
независимая переменная.
Решение. Решим пример разными способами и сравним ответы.
1-ый способ. Согласно формуле, имеем, что искомый дифференциал
Найдем все необходимые компоненты формулы. Из условия имеем:
А тогда:
2-ой
способ. Из
того, что 
и 
,
получаем:
А тогда
Найдем
вторую производную функции 
:
Окончательно имеем:
Ответ. 
34. Формула тейлора
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
Формула Тейлора
, где Rn(x) - остаточный член формулы Тейлора.
35. Функции нескольких переменных. Непрерывность. Дифференцируемость.
Введем одно важное вспомогательное понятие — понятие окрестности данной точки.
Окрестностью радиуса точки называется совокупность всех точек удовлетворяющих неравенству , т. е. совокупность всех точек, лежащих внутри круга радиуса с центром в точке .
Если мы говорим, что функция обладает каким-либо свойством «вблизи точки или «в окрестности точки , то под этим подразумеваем, что найдется такой круг с центром во всех точках которого данная функция обладает указанным свойством.
Прежде чем рассматривать понятце непрерывности функции нескольких переменных, рассмотрим понятие предела функции нескольких переменных.
Пусть дана функция
определенная в некоторой области G плоскости Рассмотрим некоторую определенную точку лежащую в области G или на ее границе (рис. 170).
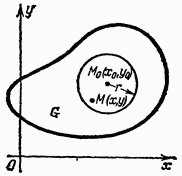
Рис. 170.
Определение 1. Число А называется пределом функции при стремлении точки к точке если для каждого числа найдется такое число что для всех точек для которых выполняется неравенство имеет место неравенство
Если число А является пределом функции при то пишут
Определение 2. Пусть точка принадлежит области определения функции Функция называется непрерывной в точке если имеет место равенство
причем точка стремится к точке произвольным образом, оставаясь в области определения функции.
Если обозначим то равенство (1) можно переписать так:
или
Обозначим . При и обратно, если , то .
Замечая, далее, что выражение, стоящее в квадратных скобках в равенстве , есть полное приращение функции равенство можно переписать в форме
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.
Если в некоторой точке не выполняется условие (1), то точка называется точкой разрыва функции Условие может не выполняться, например, в случаях:
1) определена во всех точках некоторой окрестности точки за исключением самой точки функция определена во всех точках окрестности точки но не существует предела функция определена во всех точках окрестности и существует предел но
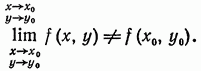
Пример 1. Функция непрерывна при любых значениях х и у, т. е. в любой точке плоскости
Действительно, каковы бы ни были числа имеем
следовательно,
Приведем пример разрывной функции.
Пример 2. Функция определена всюду, кроме точки
Рассмотрим значения t вдоль прямой Очевидно, вдоль этой прямой
т. е. функция вдоль всякой прямой, проходящей через начало координат, сохраняет постоянное значение, зависящее от углового коэффициента k прямой.
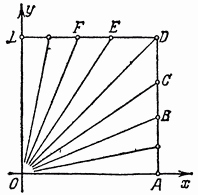
Рис. 171.
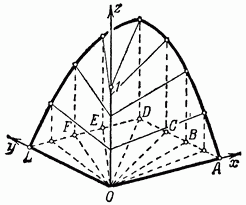
Рис. 172.
Поэтому, подходя к началу координат по различным путям, мы будем получать различные предельные значения, а это значит, что функция не имеет предела, когда точка на плоскости стремится к началу координат. Следовательно, функция разрывна в этой точке. Этуфункцию нельзя доопределить в начале координат так, чтобы она стала непрерывной. Легко видеть, с другой стороны, что в остальных точках эта функция непрерывна.
Укажем без доказательства некоторые важные свойства функции многих переменных, непрерывной в замкнутой и ограниченной области. Эти свойства аналогичны свойствам непрерывной на отрезке функции одной переменной (см. § 10 гл. II).
Свойство 1. Если функция определена и непрерывна в замкнутой и ограниченной области D, то в области D найдется по крайней мере одна точка такая, что для всех других точек области будет выполняться соотношение
и по крайней мере одна точка такая, что для всех других точек области будет выполняться соотношение
Значение функции будем называть наибольшим значением функции в области D, а значение наименьшим значением.
Это свойство формулируют и так. Непрерывная функция в замкнутой ограниченной области D достигает по крайней мере один раз наибольшего значения М и наименьшего значения
Свойство 2. Если функция непрерывна в замкнутой и ограниченной области D и если М и — наибольшее и наименьшее значения функции в области, то для любого числа удовлетворяющего условию найдется в области такая точка что будет выполняться равенство
Следствие свойства 2. Если функция непрерывна в замкнутой ограниченной области и принимает как положительные, так и отрицательные значения, то внутри области найдутся точки, в которых функция обращается в нуль.