Fizika_Labnik_Tsirkumtsizirovanny

Для определения Ex сначала измерьте потенциал в точках

(x1 − d / 2, y1) и (x1 + d / 2, y1) , где d = 20 мм, затем рассчитайте Ex по формуле

Ex ≈ − ϕ(x1 + d / 2, y1) − ϕ(x1 − d / 2, y1) . d

Аналогичным способом определите Ey :

Ey ≈ − ϕ(x1, y1 + d / 2) − ϕ(x1, y1 − d / 2) . d

4. Результаты измерений и расчетов сведите в форму табл.2.

В чем причина различий между jдиполь и jэксп ? Какое значение является более точным? В чем причина различий

между Eдиполь , Eэксп и Ex2 + Ey2 ? Какое значение является

более точным? Ответы на эти вопросы сформулируйте в виде выводов по данному упражнению.

5. Постройте с равным шагом (по потенциалу) семейство эквипотенциальных поверхностей. Картину распечатайте (или зарисуйте в тетрадь). Проведите несколько силовых линий.

Упражнение 2. Электрическое поле двух точечных зарядов произвольной величины, расположенных на расстоянии L друг от друга.

1. Постройте семейство эквипотенциальных поверхностей поля системы зарядов Q1 = Q и Q2 = 2Q . Докажите, что в

дальней зоне электрическое поле слабо отличается от поля точечного заряда. Для этого можно измерить и рассчитать

"Экспериментально" найдите потенциал точки, в которой

происходит объединение двух эквипотенциальных поверхностей в одну, охватывающую оба точечных заряда. Приняв во внимание, что в такой особой точке

напряженность электрического поля должна быть равна нулю, из уравнений

рассчитайте потенциал "критической" эквипотенциальной поверхности, проходящей через особую точку. Сравните рассчитанное значение ϕ с "экспериментальным". Картину

эквипотенциальных поверхностей распечатайте или зарисуйте.

3. (Выполняется по согласованию с преподавателем.)

Повторите п. 2 для системы зарядов Q1 = Q , Q2 = −2Q (формулы для расчета ϕ получите сами). Расстояние между

зарядами L примите равным 10, 20 или 40 мм.

Упражнение 3. Электрическое поле заряженного проводящего эллипсоида вращения (OX - ось симметрии эллипсоида вращения, a и b - большая и малая полуоси; их значения выбираются по указанию преподавателя).

1. Убедитесь, что заряд распределен по поверхности неравномерно. Для этого определите максимальную σmax и

минимальную σmin плотности поверхностного заряда на

эллипсоиде. Используйте двойной зонд и формулу (7). Обратите внимание на то, что поверхностная плотность заряда максимальна у "острых" концов эллипсоида, обладающих максимальной кривизной поверхности, и минимальна у "тупых" концов. При проведении "эксперимента" будьте внимательны: двойной зонд должен располагаться вблизи поверхности проводника, но не попадать внутрь проводника.

2.Подтвердите измерениями вывод теории: если заряд проводника увеличить в n раз, то поверхностная плотность заряда в любой точке его поверхности также увеличится в n раз. Эксперимент проведите для двух точек поверхности (например, обладающих максимальной и минимальной кривизной).

3.Закон распределения заряда по поверхности зависит от формы проводника. Убедитесь в этом, проведя измерения

σmin и σmax для эллипсоидов с различным отношением полуосей a / b . Постройте график зависимости σmax / σmin от

a / b .

4. Сформулируйте выводы.

Упражнение 4. (дополнительное). Точечный заряд вблизи нейтральной проводящей сферы.

1.Постройте семейство эквипотенциальных поверхностей.

2.Определите максимальную плотность поверхностного заряда на сфере.

3.Определите координаты точек на поверхности сферы, в которых происходит смена знака поверхностного заряда.

Подготовка к работе

1. Физические понятия, величины, законы, соотношения,

знание которых необходимо для успешного выполнения работы:

∙электрический заряд и его фундаментальные свойства;

∙плотность заряда (линейная, поверхностная, объемная);

∙закон Кулона;

∙пробный заряд; вектор напряженности электрического поля;

∙разность потенциалов; потенциал;

∙принцип суперпозиции электрических полей;

∙связь напряженности поля и потенциала;

∙электрическое поле точечного заряда;

∙электрический диполь; точечный диполь; напряженность и потенциал поля диполя;

∙теорема Гаусса;

Лабораторная работа № 3

Изучение магнитного поля на оси соленоида

Цель работы: исследование распределения индукции магнитного поля вдоль оси соленоида.

Приборы и оборудование: генератор синусоидального тока, цифровой вольтметр, соленоид, зондовая катушка, компас.

Теоретическая часть

Рассмотрим проводник, намотанный по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Если шаг винтовой линии мал по сравнению с радиусом витка, то магнитное поле соленоида можно рассматривать как результат сложения полей, создаваемых круговыми токами, расположенными рядом и имеющими общую ось.

Величина индукции магнитного поля в некоторой точке A на оси кругового тока i радиуса R (рис.1) определяется

выражением

определяющего положение точки A.

Если соленоид имеет длину l и содержит N витков, то малая часть соленоида длиной dl (рис.2,а) содержит (N / l)dl

витков и может рассматриваться как круговой ток величиной di = i(N / l)dl . С учетом того, что

dl sin ϕ = rdϕ

(рис.2,б, dϕ - бесконечно малое приращение угла ϕ ),

получим для индукции магнитного поля в точке А на оси такого "элементарного" соленоида

dB = μ0 R22nidϕ ,

2 r sin ϕ

где n = N / l - число витков, приходящихся на единицу длины соленоида. Так как R = r sin ϕ , то

Проинтегрировав выражение (2) в пределах от ϕ1 до π/2 (рис.2,в), получим индукцию магнитного поля в точке А1, лежащей на торце соленоида:

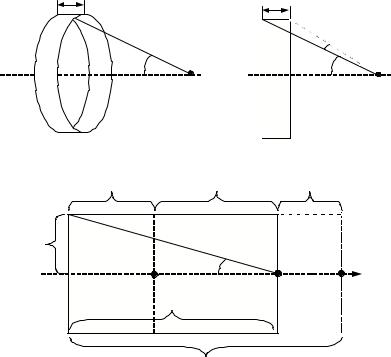
Магнитное поле в произвольной точке A, лежащей на оси соленоида внутри него, может быть вычислено как сумма полей, создаваемых соленоидами C1 и C2 (рис.2,в), а в точке A', лежащей вне соленоида, магнитное поле равно разности полей, создаваемых соленоидами С3 и С4. В результате получим:

где x > 0 вне соленоида и - l < x < 0 внутри соленоида.

Из выражения (3) следует, что в центре соленоида ( x = -l / 2 )

индукция магнитного поля равна

В случае длинного соленоида ( 4R2 / l2 << 1) магнитное поле в его центральной части слабо зависит от x ( B » m0ni ) и

начинает заметно уменьшаться лишь на расстояниях (2…3)R от торцов соленоида. На торце длинного соленоида индукция магнитного поля становится равной m0ni / 2 .

Формула (3) справедлива не только для постоянных i и B, но

идля мгновенных значений изменяющихся во времени тока

имагнитного поля, если только их изменения не происходят слишком быстро (для квазистационарных токов). В

частности, если ток через соленоид меняется по закону i = Im cos wt , то по такому же закону меняется и магнитное

поле B = Bm cos wt , причем амплитудные значения тока Im и магнитного поля Bm на оси соленоида связаны формулой (3), в которой i = Im , B = Bm .

Описание эксперимента

Измерения магнитного поля в данной работе проводятся на переменном токе и основаны на законе электромагнитной индукции. Электрическая схема установки приведена на рис.3. Магнитное поле в соленоиде создается переменным