2. Дифракция рентгеновских лучей на кристалле и обратная решетка

Дифракция волн на решетке может наблюдаться, если длина волны  сравнима по величине с расстоянием между соседними атомами в решетке. При падении волны на кристалл каждый атом (или, точнее, каждый электрон в атоме) становится источником вторичного излучения. Вторичные лучи интерферируют и формируют отраженное излучение. Если разность фаз для отраженных лучей составляет m, то в результате интерференции возникают дифракционные максимумы.

Условие формирования дифракционного максимума можно получить, вычислив разность фаз для двух лучей (1 и 2), отраженных в заданном направлении от двух произвольных атомов решетки, разнесенных на вектор R (рис. 1). Разность фаз  определяется разностью хода l, проходимой лучами, умноженной на модуль волнового вектора излучения который не меняется по величине при упругом рассеянии.

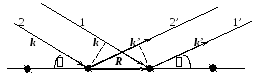
Рис.1. Дифракция лучей на решетке (построение Лауэ)

На рис.1 k и k’ - волновые векторы падающего и отраженного излучений. Из рис. 1 следует, что

где и - углы между вектором трансляции R, соединяющим атомы, и направлениями падающей (k) и отраженной (k’) волн, соответственно. С учетом соотношений

и

условие для возникновения максимума можно записать в виде:

(2)

где т - произвольное целое число.

Соотношение (2) называется условием Лауэ.

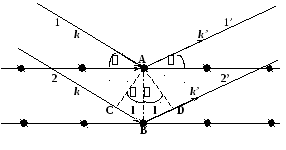
Рис.2. Дифракция лучей на решетке (построение Брэгга)

Условие дифракции можно также получить, если представить кристалл состоящим из набора параллельных атомных плоскостей, от которых происходит зеркальное отражение падающей волны (рис. 2). Дифракционный максимум в направлении отраженной волны будет наблюдаться, если разность хода для лучей 1 и 2, отраженных от соседних плоскостей, будет равна целому числу длин волн. На рис. 2 угол между направлением падающей волны и плоскостью отражения (угол падения) обозначен через , а расстояние между соседними плоскостями через d, линии АС и AD - проекции плоскости волнового фронта (поверхности постоянного значения фазы) до и после отражения. Линии АС и AD перпендикулярны, k и k’, соответственно. Из решения прямоугольных треугольников ABC и ABD можно найти разность хода и записать условие (2) в виде

.

(3)

Условия Лауэ (2) и Вульфа-Брэгга (3), как будет показано ниже, эквивалентны. Поскольку вектор R, соединяющий два узла решетки, есть период решетки и может принимать дискретный набор значений (1), то из (2) следует, что при заданном волновом векторе падающей волны k, отраженная волна может распространяться в направлениях, тоже образующих дискретный набор. Обозначим вектором G изменение волнового вектора при рассеянии.

.

(4)

Тогда множество векторов G, удовлетворяющих условию (2), определяется соотношением

(5)

и образует бесконечную решетку, которая называется обратной решеткой. Размерность векторов обратной решетки - [длина^-1]. Обратная решетка - совокупность узлов в обратном пространстве или в пространстве волновых векторов. Как и в любой решетке, в обратной решетке можно выделить векторы примитивных трансляций b_i и записать произвольный вектор обратной решетки G в виде

(6)

где (h, k, l) - произвольный набор целых чисел. Чтобы условие (5) выполнялось, необходимо в качестве векторов b_i выбрать векторы, связанные с элементарными трансляциями a_i прямой решетки следующими соотношениями.

(7)

где  - объем примитивной элементарной ячейки прямой решетки.

Отметим некоторые свойства обратной решетки.

1. Векторы обратной решетки b_i удовлетворяют условию

.

(8)

В этом легко убедиться, используя формулу (7) и правила вычисления произведений векторов.

2. Любой системе параллельных плоскостей прямой решетки с индексами Миллера h, k, l можно поставить в соответствие вектор G_hkl обратной решетки, перпендикулярный этим плоскостям, причем модуль вектора G_hkl связан с межплоскостным расстоянием d_hkl соотношением

.

(9)

Среди целых h, k, l не должно быть общего множителя.

3. Индексы Миллера плоскости (hkl) и вектора G_hkl, перпендикулярного им, совпадают. Индексы Миллера плоскости определяются следующим образом. Пусть плоскость отсекает от осей координат отрезки P₁, P₂, P₃. Находят целые числа n₁, n₂,, и n₃, равные 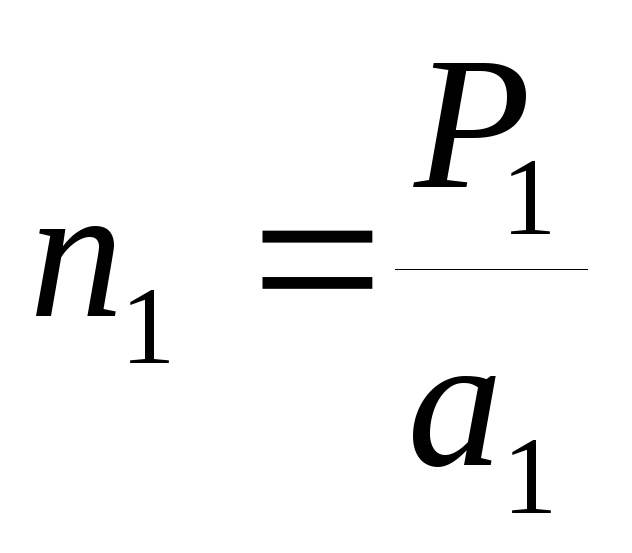,,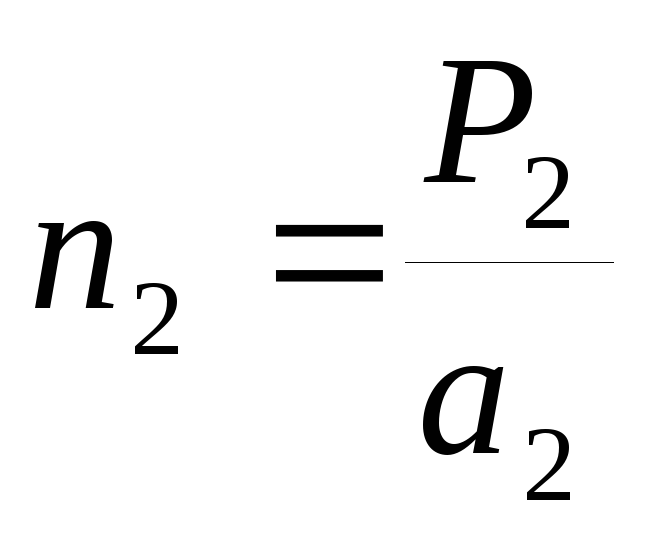,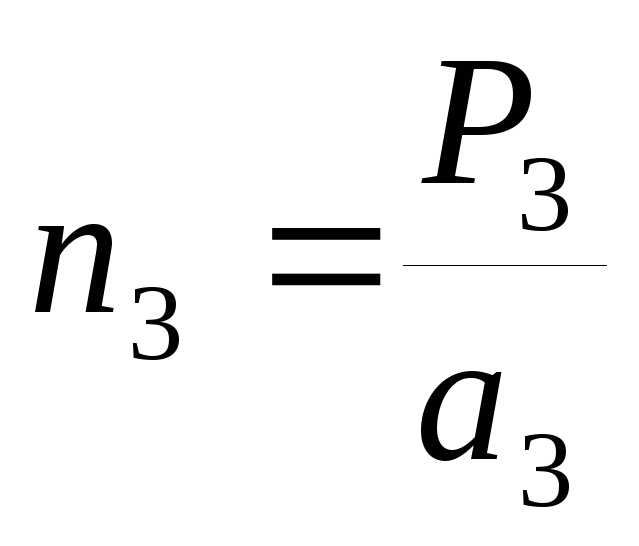затем определяют обратные числа 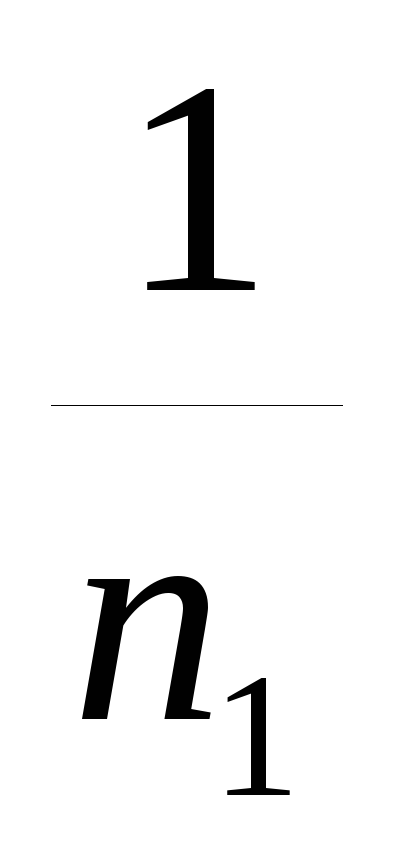, 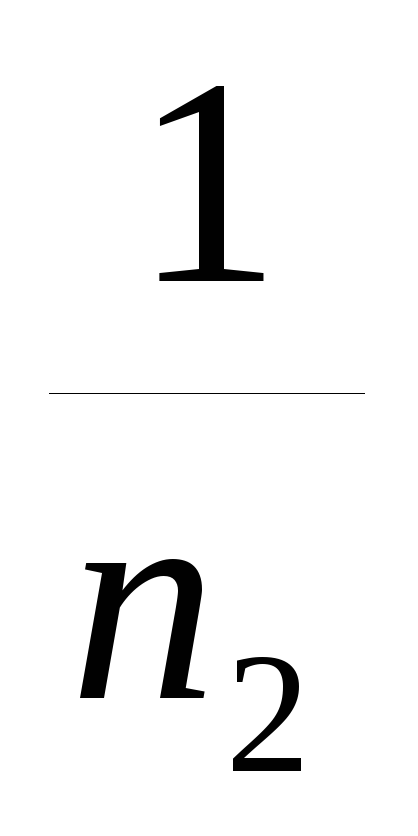и 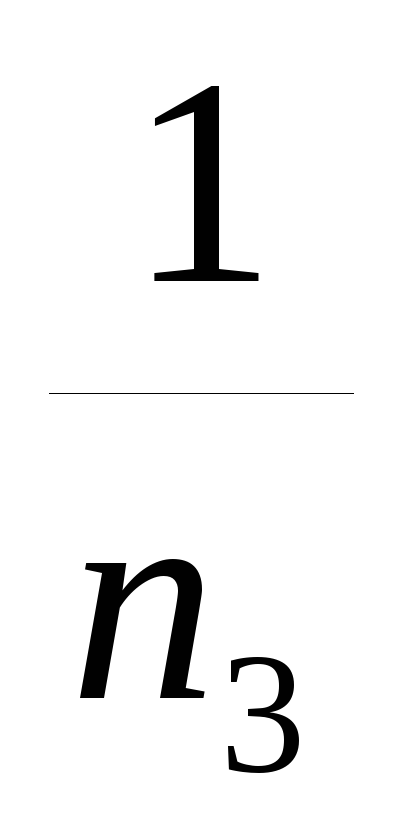,приводят их к общему знаменателю и знаменатель отбрасывают. Тройка целых чисел, не содержащих общего множителя и есть индексы Миллера плоскости (hkl), то есть

.

Вектор G, перпендикулярный плоскости (hkl), ортогонален любому вектору R, принадлежащему этой плоскости. Учитывая, что скалярное произведение (GR)=0, легко убедиться, что индексы Миллера вектора (k’)²= (k)к² + 2kG + G² совпадают с индексами (hkl) плоскости, ему перпендикулярной.

Закон Вульфа-Брэгга (3) и условия Лауэ (2) эквиваленты. В самом деле, из равенств (2) и (4) следует, что

.

(10)

Или

.

(11)

Учитывая, что при упругом отражении , имеем

.

(12)

Взаимное расположение векторов k и G представлено на рис.3.

Так как и , получим из (12)

,

то есть , или , что и есть закон Вульфа-Брэгга (3).

Рис.3. Связь между векторами k, k’ и G в условиях дифракции Лауэ

Из условия Лауэ следует, что если известны направления дифракции рентгеновских лучей, то, зная длину волны падающего излучения, по ним можно восстановить часть векторов обратной решетки. Таким образом в дифракционном эксперименте непосредственно определяется обратная решетка, с которой однозначным образом связана прямая решетка.