
2
.pdf
Определение постоянной интегрирования:
u |
(0) |
E |
m |
X |
c sin( 90o ) A |
0 |
||||
|
|
|||||||||
C |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E X |
С |
o |
|
|
||
|
|
|
|
|
m |
|
. |
|||
|
A |
|
|
Z |
|
sin( 90 |
) |
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
;
Как следует из полученного уравнения, амплитуда свободной состав-
ляющей |
A |
зависит от |
начальной |
фазы |
источника ЭДС. При |
|
|
||||||
|
|
|
|
|
|
|
90 |
90 |
эта |
амплитуда |
имеет |
максимальное значение |
|
|
|
|
||||
A Amax |
Em X С |
, при этом переходной процесс протекает с максимальной |
|
||
|
Z |
|
|
90 |
0 |
|
интенсивностью. При |
|
|
амплитуда свободной составляю- |
|
|
щей равна нулю и переходной процесс в цепи отсутствует.
19. Анализ переходных процессов в цепи R, L, C
Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом источника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес представляют свободные составляющие, так как характер свободного процесса оказывается существенно различным в зависимости от того, являются ли корни характеристического уравнения вещественными или комплексными сопряженными.
Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 22).
i |
R |
|
L |
C |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 E
E
Рис. 22
Общий вид решения для тока:
i(t) iy (t) icв (t) Iy A1e p2t A2e p2t .
Установившаяся составляющая: I y 0 .
41
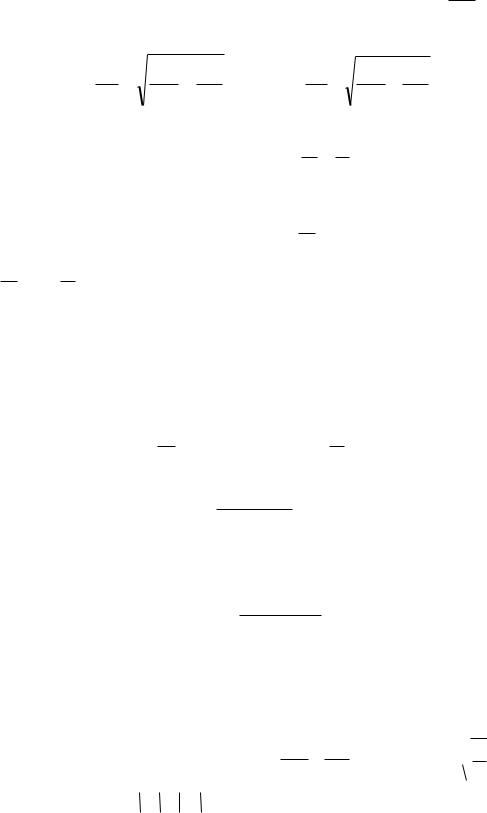
Характеристическое уравнение и его корни:
откуда:
|
|
R |
|
R |
2 |
|
1 |
|
|
|
R |
|
p |
|
|
|
|
; |
p |
|
|
||||
|
|
2 |
|
|
||||||||
1 |
|
2L |
|
|
|
LC |
2 |
|
2L |
|
||
|
|
|
4L |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
Z ( p) pL |
|||
R |
2 |
|
1 |
|
|
||
|
2 |
LC |
|
|
|
||
4L |
|
||
.
1 pC
R
0
,
Дифференциальное уравнение: |
|
iR L |
di |
|
1 |
|
idt E |
. |
|
|||||||||
|
dt |
C |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Независимые начальные условия: |
i(0) |
0 |
; |
u |
C |
(0) 0 |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
Зависимое начальное условие: |
i(0)R L |
di |
(0) u |
|
(0) E |
; |
||||||||||||
dt |
C |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда |
di |
(0) |
|
E |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Постоянные интегрирования определяется из совместного решения системы уравнений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
A |
0 |
|
|
|
|
|||
|
i(0) |
|
|
|
|
|||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
di |
(0) |
p A p |
|
A |
|
E |
|||||
|
|
2 |
|
|||||||||
|
|
|
|
1 1 |
|
|
|
2 |
|
L |
||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
откуда |
A A |
|
E |
|
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
||||||
1 |
|
2 |
( p p |
)L |
|
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
Окончательное решение для тока:
i(t) A e p2t A e p2t |
|
1 |
2 |
|
E |
|
(e |
p t |
p |
|
1 |
||
( p |
2 |
)L |
|
|
1 |
|
|
|
e |
p |
2 |
t |
) |
|
|
.
Исследуем вид функции i(t) при различных значениях корней характеристического уравнения.
а) Корни характеристического уравнения вещественные, не равны
друг другу. Это имеет место при условии
R |
2 |
|
1 |
|
|
|
0 |
||
|
2 |
LC |
||
|
|
|
||
4L |
|
|
||
или R 2
 CL , тогда
CL , тогда
p 0 |
, |
p |
0 |
, причем |
p p |
, |
p p 0 |
. |
||
1 |
2 |
|
1 |
2 |
1 |
2 |
||||
При изменении t от 0 до ∞ отдельные функции e p1t и e экспоненциальному закону от 1 до 0, причем вторая из них
рее, при этом их разность e p1t e p2t 0 . Из этого следует комая функция тока i(t) в крайних точках при t = 0 и при t =
p |
t |
|
2 |
|
убывают по |
|
|
убывает быст-
вывод, что ис- ∞ равна нулю,
42
а в промежутке времени 0 < t котором значении времени Найдем этот момент времени:
< ∞
t |
m |
|
всегда положительна, достигая при
своего максимального значения |
I |
|
не-
max .
di dt
E |
|
|
p t |
|
|
|
( p e 1 m |
L( p p |
|
) |
1 |
2 |
|
||
1 |
|
|
p e |
p |
t |
) |
|
2 m |
||||
2 |
|
|||
|
|
|
||
0
, или
|
p t |
p t |
p e 1 m p e |
2 m |
|
1 |
2 |
|
0
,
откуда
Графическая
|
|
|
|
p |
|
|
|
ln |
2 |
|
|
|
|
p |
|
||
t |
|
|
|
|
|
m |
|
1 |
. |
||
|
p |
p |
|||
|
|
||||
|
|
|
|||
|
|
1 |
|
2 |
|
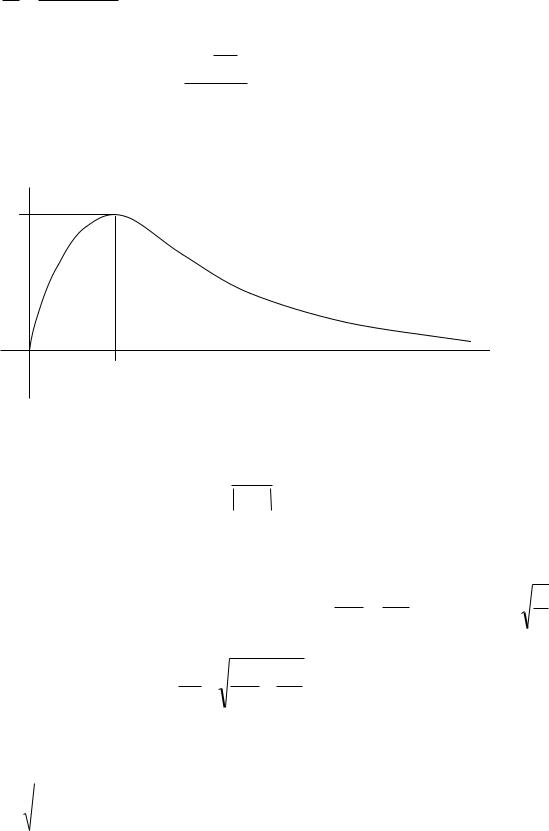
диаграмма функции
i(t)
для случая вещественных кор-
ней характеристического уравнения показана на рис. 23. i
Imax
tm t
Рис. 23
Продолжительность переходного процесса в этом случае определяется
меньшим по модулю корнем:
T |
|
4 |
|
||
п |
|
p |
|
|
|
|
|
min |
.
Характер переходного процесса при вещественных корнях характеристического уравнения получил название затухающего или апериодического.
б) Корни характеристического уравнения комплексно сопряженные.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
2 |
|
|
1 |
|
|
|
Это имеет место при соотношении параметров |
|
|
|
0 |
или |
||||||||||||||||||||
|
|
2 |
LC |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4L |
|
|
|
||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
b |
j |
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1,2 |
|
2L |
|
|
|
LC |
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
4L |
|
|
|
|
|
|
|
|
|
|
|||
где b |
|
R |
коэффициент затухания, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2L |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
R |
|
угловая частота собственных колебаний. |
||||||||||||||||||
|
LC |
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
4L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 |
L |
|
C |
||
|
,
43
Решение для исконной функции может быть преобразовано к другому виду:
i(
t) |
|
|
E |
e |
p t |
e |
p |
t |
|
|
E |
|
|
|
|
e |
b j |
|
e |
b j |
|
|
|||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
||||||||||
|
|
p p |
L |
|
|
|
b j b j |
L |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ee |
bt |
cos t j sin t cos t j sin t |
E |
|
bt |
|
|
|
|
|
bt |
|
|
|
|
||||||||||||
|
|
e |
sin t |
Ae |
sin |
t |
. |
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 j L |
|
|
0 |
|
0 |
|
|
|
0 |
0 |
|
L |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, в случае комплексно сопряженных корней характери-
стического уравнения искомая функция
гармоническому закону |
I |
m |
sin t |
|
0 |
i(t)
с
изменяется во времени по затухающей амплитудой
I |
m |
(t) |
|
|
Ae |
bt |
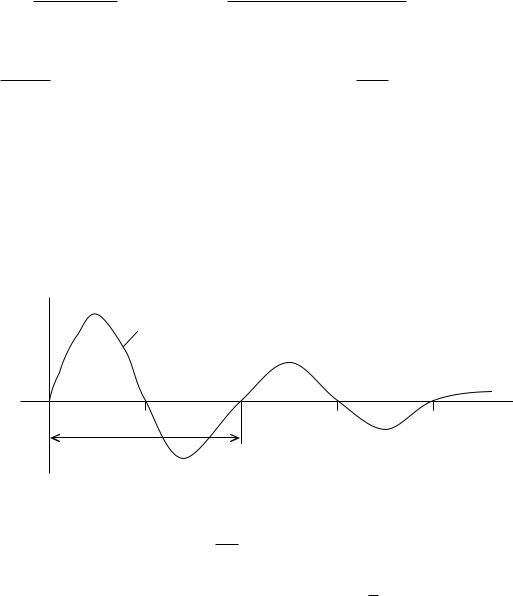
. Графическая диаграмма функции |
|
||
|
|
i
i(t)
T0
i(t)
показана на рис. 24.
t
|
|
|
|
Рис. 24 |
|
|
|
|
Период колебаний |
T |
|
2 |
, продолжительность переходного процес- |
||||
|
||||||||
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
са определяется коэффициентом затухания: |
T |
|
4 |
. |
||||
|
||||||||
n |
|
b |
||||||
|
|
|
|
|
|
|
|
|
Характер переходного процесса при комплексно сопряженных корнях характеристического уравнения получил название колебательного или периодического.
В случае комплексно сопряженных корней для определения свободной составляющей применяют частную форму:
xсв(t) Ae bt sin 0t или xсв (t) e bt B sin 0t C cos 0t ,
где коэффициенты A и или B и C являются новыми постоянными интегрирования, которые определяются через начальные условия для искомой функции.
44

в) Корни характеристического уравнения вещественные и равны друг
другу. Это имеет место при условии
тогда p1 p2 p 2RL .
R |
2 |
|
1 |
|
|
|
0 |
||
|
2 |
LC |
||
|
|
|
||
4L |
|
|
||
или R 2
 CL Rkp ,
CL Rkp ,
Полученное ранее решение для искомой функции |
i(t) |
в этом случае |
|
|
становится неопределенным, так как числитель и знаменатель дроби превращаются в нуль. Раскроем эту неопределенность по правилу Лопиталя,
считая |
p |
p const |
, а |
p |
var |
, которая стремится к |
p |
. Тогда получим: |
2 |
|
1 |
|
|
|
E |
|
|
e |
p t |
e |
pt |
|
E |
|
|
te |
p t |
i(t) |
|
|
1 |
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
||||
L |
lim |
|
p |
p |
L |
lim |
1 |
||||||
|
1 |
p |
|
|
1 |
p |
|||||||
|
|
p |
|
1 |
|
|
|
|
p |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E te pt L
Ate |
pt |
|
.
Характер переходного процесса при равных корнях характеристического уравнения получил название критического. Критический характер переходного процесса является граничным между затухающим и колебательным и по форме ничем не отличается от затухающего. Продолжитель-
ность переходного процесса |
T |
4 |
|
. При изменении только сопротивле- |
||||||
п |
|
p |
||||||||
|
|
|
|
|
|
|
|
|
|
|
ния резистора |
R var |
0 |
затухающий характер переходного процес- |
|||||||
|
|
|
|
|||||||
са соответствует области значений |
|
Rvar (Rкр Rvar ) , колебательный |
||||||||
характер – также области значений |
(0 R |
R |
) |
, а критический харак- |
||||||
|
var |
кр |
|
|||||||
тер – одной точке |
R |
R |
. Поэтому на практике случай равных корней |
|||||||
var |
кр |
|||||||||
характеристического уравнения встречается крайне редко.
В случае равных корней для определения свободной составляющей применяют частную форму:
|
|
|
x |
(t) ( A A t)e |
pt |
, |
||
|
|
|
|
|||||
|
|
|
|
св |
1 |
2 |
|
|
где коэффициенты |
A |
и |
A |
являются новыми постоянными интегрирова- |
||||
1 |
2 |
|||||||
ния, которые определяются через начальные условия для искомой функции.
Критический режим переходного процесса характерен тем, что его
продолжительность имеет минимальное значение
|
|
2 |
4 |
|
T |
|
|
||
|
п min |
|
p |
|
|
|
|
кр |
|
|
|
|
||
4R L
.
Указанное свойство находит применение в электротехнике.
20. Переходные функции по току и напряжению
Пусть произвольная электрическая цепь с нулевыми начальными условиями [iL (0) 0, uC (0) 0] в момент времени t 0 включается под действием источника постоянной ЭДС e(t) E const (рис. 25).
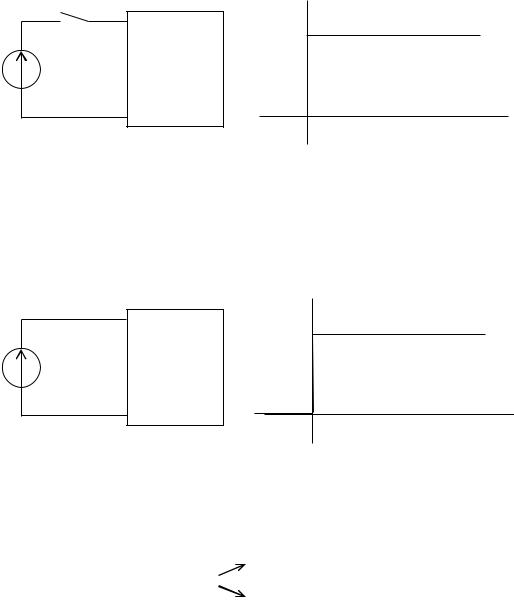
t = 0 |
|
|
e(t) = E = const |
|
iL(0)=0 |
E |
uC(0) =0 |
|
|
|
t |
а |
б |
|
Рис. 25 |
Переходной процесс не изменится, если из схемы убрать ключ, а по-
стоянную ЭДС |
e(t) E const |
заменить скачкообразной |
e(t) E 1(t) |
со |
|
|
скачком в момент
t 0
(рис. 26).
e(t) = E = const
iL(0)=0
e(t)
uC(0) =0
t
а |
б |
Рис. 26
Функция 1(t ющей значения:
)
называется единичной
1(t) |
0 при |
t |
|
||
|
t |
|
|
1 при |
|
|
|
скачкообразной функцией, име-
00
Возникающие на любых участках цепи токи
прямо пропорциональны скачкообразной ЭДС |
e(t |
|
)
ik (t)
E
и напряжения uk (t)
1(t) |
: |
|
|
|
|
i |
|
(t) e(t) h (t) e(t) g(t) |
|
|
|
|
k |
|
i |
|
|
|
|
u |
k |
(t) e(t) h (t) e(t) k(t) |
|
|
|
|
|
u |
||
где |
h (t) g(t) |
переходная функция по току, или переходная проводи- |
||||
i |
|
|||||
|
|
|
мость, |
|
|
|
|
h |
(t) k(t) |
переходная функция по напряжению. |
|||
|
u |
|
||||
Переходная функция по току |
g(t) |
или по напряжению |
k(t) называет- |
|
ся функция по времени, численно равная соответствующему току i(t) или напряжению u(t) при включении цепи с нулевыми начальными условиями к источнику единичной постоянной e(t) E 1(t) . Переходные функции
46
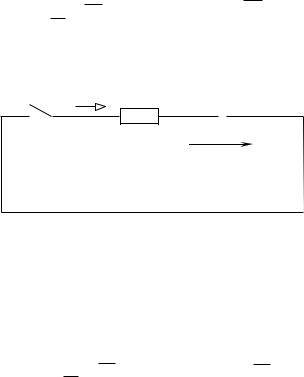
g(t)
и
k(t)
могут быть рассчитаны для любой схемы классическим или
операторным методом.
Пример. Рассчитать переходные функции для тока
u |
C |
(t) |
в цепи R, С. |
|
|
i(t)
и напряжения
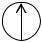
Решение. Выполним расчет переходного процесса в цепи R, C при включении ее к источнику постоянной ЭДС e(t) E (рис. 27) классическим методом. В результате найдем:
i(t)
 E
E
E |
|
|
t |
|
e |
RC |
|||
|
|
|||
R |
|
|
||
|
|
|
i
;
u |
(t) |
C |
|
R
|
|
|
|
t |
E 1 |
e |
RC |
||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
uC |
|
||
.
Рис. 27
Искомые переходные функции получим из найденных выражений, заменив в них Е на 1.
g(t)
1 |
|
t |
|
RC |
|||
|
e |
||
|
|
||
R |
|
|
;
|
|
t |
|
k(t) 1 e |
RC |
||
|
|||
|
|
.
Переходные функции используются при расчете переходных процессов методом интеграла Дюамеля.
21. Расчет переходных процессов методом интеграла Дюамеля
Метод интеграла Дюамеля применяется для расчета переходных процессов в электрических цепях в том случае, если в рассматриваемой цепи действует источник ЭДС u(t) произвольной формы, отличной от стандартной (постоянной или синусоидальной).
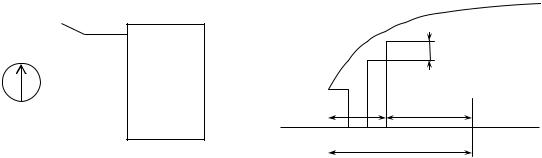
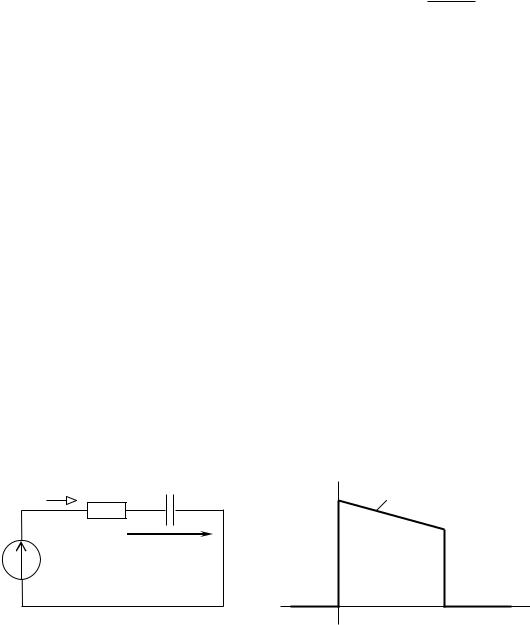
Пусть к источнику ЭДС произвольной формы u(t) подключается цепь с нулевыми начальными условиями и с заданной переходной проводимостью g(t) (рис. 28).
47
|
t = 0 |
|
|
|
|
e |
u(t) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
u |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t) |
П |
|
|
u(0) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
t – |
t |
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
а |
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Рис. 28 |
|
|
|
|
|
|
|
|
|
Заменим непрерывную кривую ЭДС u(t) приближенно ступенчатой с |
|||||||||||||||
интервалами по оси |
t между отдельными скачками, |
равными . Первый |
|||||||||||||
скачок ЭДС равен u(0) |
и действует в момент t = 0. Все последующие |
||||||||||||||
скачки ЭДС можно определить как |
u tg e ( ) |
и действуют |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||
они с запаздыванием на , то есть в момент t – . Ток на выходе цепи в произвольный момент времени t можно рассматривать в соответствии с принципом наложения как сумму частичных токов, возникающих под действием отдельных скачков ЭДС, следующих друг за другом через проме-
жутки |
|
в интервале времени от 0 до t. |
|
|
|
|
|
|
|||
Частичный ток, вызванный первым источником ЭДС, будет равен |
|||||
i (t) u(0) g(t) |
|
последующими скачками |
|||
|
|
, а частичные токи, вызванные |
|||
ЭДС, будут равны: |
i (t) u g(t ) u ( ) g(t ) |
. |
|||
|
|
||||
Результирующий ток равен сумме частичных токов:
t i(t) i (t) i
0
Перейдем к бесконечно интегралом:
t(t) u(0) g(t) u ( ) g(t)
0
малым интервалам d
.
и заменим сумму
t i(t) u(0) g(t) u ( ) g(t
)d
.
|
|
0 |
Полученное выражение для |
i(t) |
носит название интеграла Дюамеля и |
|
применяется на практике для расчета переходных процессов в электрических цепях при воздействии на них источников ЭДС или тока произвольной формы.
Порядок применения интеграла Дюамеля:
1) Выполняют расчет переходного процесса классическим или операторным методом при включении исследуемой цепи к источнику единичной
48
постоянной ЭДС |
E 1 и таким образом определяют необходимую пере- |
||||||||||||||||||||
ходную функцию по току g(t) или по напряжению |
k(t) |
. |
|
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
2) |
Определяют переходную функцию |
g(t ) |
или k(t ) путем за- |
|||||||||||||||||
мены в выражениях g(t) |
или |
k(t) |
переменной t |
на t . |
|
|
|||||||||||||||
|
3) |
Находят производную от функции ЭДС |
u (t) |
d u(t) |
и в получен- |
||||||||||||||||
|
dt |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ном выражении заменяют переменную t на , в результате получают функ- |
|||||||||||||||||||||
цию |
e ( ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
) |
|
g(t ) |
|
|
|
k(t ) |
|
|
||
|
4) |
Выражения функций |
u ( |
, |
или |
|
подставляют в |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
формулу интеграла Дюамеля, выполняют интегрирование по переменной |
|||||||||||||||||||||
и подставляют пределы интегрирования по переменной t. При необходи- |
|||||||||||||||||||||
мости упрощают структуру полученного выражения искомой функции i(t) |
|||||||||||||||||||||
или |
u(t) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Замечания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1) |
Если функция |
u |
(t) |
претерпевает скачки или разрывы, то она раз- |
||||||||||||||||
|
|
|
|||||||||||||||||||
бивается на отдельные участки с плавным изменением функции, при этом |
|||||||||||||||||||||
интеграл Дюамеля применяется к каждому участку в отдельности. |
|||||||||||||||||||||
|
2) |
При расчете переходных процессов в цепях постоянного или сину- |
|||||||||||||||||||
соидального тока метод интеграла Дюамеля проигрывает классическому и |
|||||||||||||||||||||
операторному методам, поэтому для таких цепей он не применяется. |
|||||||||||||||||||||
|
Пример. Рассчитать ток |
i(t) |
в цепи R, C при действии на нее трапе- |
||||||||||||||||||
|
|
||||||||||||||||||||
циевидного импульса с заданными параметрами (рис. 29): |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
i |
|
R |
|
C |
|
|
|
|
u(0) |
|
|
u(t) = u(0) kt |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e(t1) |
|||
|
|
|
|
uC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 29 |
|
|
|
|
|
|
|
|
||
|
Решение. Переходная проводимость схемы: |
|
|
|
|
|
|||||||||||||||
|
1 |
e |
t |
|
1 |
e |
t |
|
1 |
e |
t |
|||||
g(t) |
|
; |
g(t ) |
rC |
|
RC |
e |
RC |
. |
|||||||
rC |
||||||||||||||||
|
|
|
||||||||||||||
|
R |
|
R |
|
R |
|||||||||||
49

|
|
|
|
|
u(t) |
|
u (t) k |
|
|
|
||||
Производная от функции ЭДС |
: |
; |
u ( ) k |
. |
||||||||||
|
|
|
|
|
|
|
||||||||
Так как функция |
u(t) |
в момент времени |
t t |
изменяется скачком, то |
||||||||||
|
|
|
1 |
|||||||||||
ее разбиваем на два участка |
0 t , |
|
t |
|
, для каждого из которых |
|||||||||
|
1 |
|
1 |
|
|
|||||||||
находим свое решение для искомой функции |
|
i(t) |
. |
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
Решение для |
0 t t |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
t |
|
|
t |
|
1 |
|
|
t |
|
|
|
|
|
|
e(0) |
|
t |
|
|
k |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
i(t) u(0) |
e |
RC |
|
|
k |
e |
RC |
e |
RC |
d |
e |
RC |
|
e |
|
RC |
|
RCe |
RC |
|||||||||||||
R |
|
R |
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
e(0) |
|
|
|
|
|
t |
|
|
|
|
|||
u |
e(0) |
e |
RC |
kCe |
|
RC |
|
e |
RC |
|
kC |
RC |
kC . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
e |
|
|
|
|||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение для |
t |
|
t |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i(t) u(0)g(t) |
1 |
u ( ) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
g(t ) d u(t |
) g(t t |
) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
||
|
|
|
|
||
|
||
|
0 |
|
|
.
22. Расчет переходных процессов в цепи при воздействии на нее ЭДС e(t) произвольной формы.
Расчет переходных процессов в цепи при воздействии на нее ЭДС e(t) произвольной формы, отличной от стандартной (постоянной или синусоидальной), может быть выполнен также численным методом на ЭВМ основе стандартных программ. Рассмотрим применение данного метода на конкретном примере.
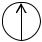
Пусть на цепь RLC (рис. 30) с заданными параметрами элементов в момент t = 0 действует напряжение импульсной формы (рис. 31).
i |
R |
L |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 e(t)
e(t)
Рис. 30
50
