2

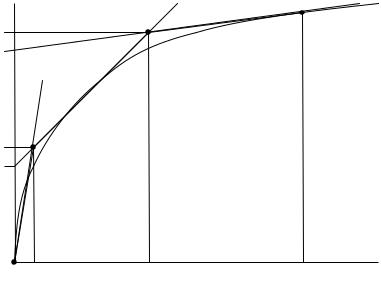
решены известными методами (классическим или операторным). При переходе от одного участка к другому в дифференциальных уравнениях будут скачком изменяться постоянные коэффициенты, что повлечет скачкообразное изменение коэффициентов в их решении. Решения для отдельных участков сопрягаются между собой на стыках участков на основе законов коммутации.

Рассмотрим применение данного метода к расчету переходного процесса при включении нелинейной катушки к источнику постоянной ЭДС Е (рис. 97, а). Нелинейную вебер-амперную характеристику катушки (i) заменим отрезками прямой линии (ломаной линией 0-1-2-3) (рис. 98):

Аппроксимируем отдельные отрезки ломаной линии уравнениями

диаграммы, а коэффициенты L1, L2, L3 через координаты точек стыка от-

резков (0,1, 2, 3):

Дифференциальные уравнения для отдельных участков будут иметь

вид:

131

Решения уравнений для отдельных участков, найденные классическим методом, будут отличаться только постоянными коэффициентами:

Постоянные интегрирования находятся из начальных условий и законов коммутации:

1)при t = 0, i1(0) = 0, из решения (1) следует A1 = Iy,

2)при t = t1, i2(t1) = I1, из решения (2) следует A2 = I1 Iy,

3)при t = t2, i3(t2) = I2, из решения (3) следует A3 = I2 Iy.

Моменты времени t1, t2, соответствующие переходу процесса с одного участка характеристики на другой, определяются из совместного решения уравнений для смежных участков в точке стыка:

Графическая диаграмма переходного процесса показана на рис. 99. Наличие изломов на графической диаграмме искомой функции i(t) объясняется погрешностями аппроксимации характеристики нелинейного элемента возле точек стыка отдельных участков. Достоинство данного метода состоит в том, что он позволяет применить к расчету переходных процессов в нелинейных цепях известные методы расчета переходных процессов в линейных цепях.

132

Iy i

2

I2

1

I1

Рис. 99

4. Расчет переходного процесса методом линеаризации дифференциального уравнения

Сущность данного метода заключается в том, что в нелинейном дифференциальном уравнении, описывающем переходной процесс, пренебрегают нелинейностью второстепенных членов этого уравнения, при этом функциональные коэффициенты в этих членах заменяются постоянными. После такой замены нелинейное дифференциальное уравнение превращается в линейное и решается известными методами (классическим или операторным).

Рассмотрим применение данного метода на примере расчета переходного тока в трансформаторе при его включении на холостом ходу к источ-

iR d Um sin( t ) dt

Так как активное сопротивление R обмотки трансформатора незначи-

тельно, то d iR и второе слагаемое iR можно считать второстепенным dt

членом этого уравнения.

Выразим i L , где L = f (i, ) – функциональный коэффициент, тогда дифференциальное уравнение цепи получит вид:

133

Заменим функциональный коэффициент L = f(i, ) в последним уравнении некоторым постоянным значением L = Lст= const, после чего дифференциальное уравнение цепи становится линейным относительно переменной . Решение этого уравнения может быть получено классическим методом:

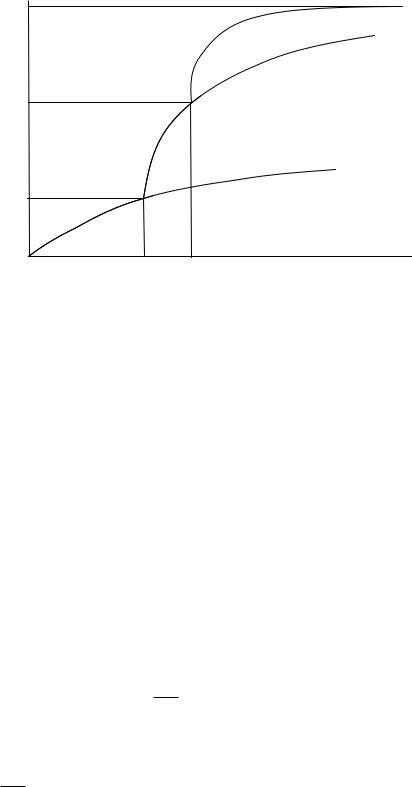
амплитуда свободной составляющей А зависит от начальной фазы напряжения источника. При = 90 она имеет максимальные значения, переходной процесс при этом протекает с максимальной интенсивностью. Пусть = 90 , тогда А = Ψm и решение для функции (t) получит вид:

m

Рис. 100

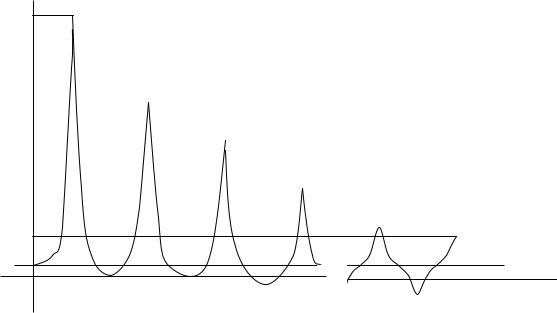
Графическую диаграмму искомой функции i(t) можно построить методом проекции расчетной функции (t) на вебер-амперную характеристику i( ) (рис. 100, а, б). Эта диаграмма представлена на рис. 101:

134

i

Imax

Как показывает анализ полученного решения, амплитуда первой волны потокосцепления практически равна удвоенному номинальному значе-

нию: max 2 m . Эта точка 1 на вебер-амперной характеристике i( ) находится далеко в области насыщения и ей соответствует ток Imax, значи-

ного тока. Такой импульс пускового тока совершенно не опасен для динамической или термической устойчивости трансформатора, однако он может вызвать ложное срабатывание его релейной защиты. По этой причине мощные силовые трансформаторы запрещается включать в сеть в режиме холостого хода. При включении в сеть нагруженного трансформатора переходной процесс быстро затухает, при этом амплитуда импульса пускового тока незначительна.

5. Расчет переходного процесса методом численного интегрирования дифференциального уравнения

Режим нелинейной цепи любой сложности может быть описан системой нелинейных дифференциальных уравнений, составленных для схемы цепи по законам Кирхгофа. Как известно из математики, система дифференциальных уравнений (как линейных, так и нелинейных) может быть решена методом численного интегрирования (методы Эйлера, РунгеКутта). Таким образом, режим любой нелинейной цепи может быть рассчитан методом численного интегрирования дифференциальных уравнений.

135

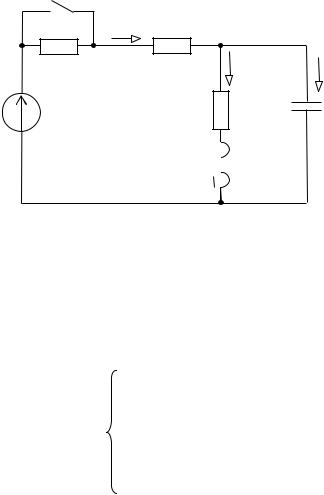
Рассмотрим применение этого метода на примере расчета схемы рис. 102.

i2( )

Рис. 102

Пусть на входе схемы источник постоянной ЭДС Em, а веберамперная характеристика нелинейной катушки аппроксимирована уравнением i = a·sh(b· ). Система дифференциальных уравнений, составленных для схемы цепи по законам Ома и Кирхгофа и дополненная нелинейным алгебраическим уравнением аппроксимации характеристики нелинейного элемента, будет иметь вид:

Решение этой системы уравнений может быть выполнено методами численного интегрирования на ЭВМ (например, методом Эйлера). Суть метода состоит в том, что период переменного тока Т разбивается на большое число шагов интегрирования, например N = 1000, дифференциалы переменных заменяются конечными приращениями (d , duu, di i, dt t), а производные переменных отношением приращений (d /dt / t, du/dt u/ t). На каждом шаге производится решение системы уравнений и определяются значения переменных величин (токов, напряжений) и их производных, причем в качестве исходных данных принимают значения некоторых переменных на предыдущем шаге. В качестве таких функций принимают uС(t), iL(t), которые определяют запасы энергии в электрическом и магнитном поле, вследствие чего они не могут изменяться скачкообразно. Непосредственным результатом расчета будут являться массивы значений переменных величин (токов, напряжений) и их производных в заданном интервале времени (например, в течение времени переходного процесса Тп). В результате последующей обработки массивов данных могут быть определены все параметры функций.

Один из вариантов решения полученной системы уравнений методом численного интегрирования представлен ниже.

136

Исходные данные: параметры элементов схемы (E, R1, R2, C, a, b); начальные условия uС(0) = 0, (0) = 0.

Принимаем: N число шагов интегрирования, Т – расчетное время

k = (k-1) + h · (d /dt) k; uСk =uС(k-1) + h · (duС /dt) k .

Метод численного интегрирования (численный метод) обладает высокой точностью, так как в нем непосредственно используются физические характеристики нелинейных элементов. С появлением ЭВМ и расширением области их применения данный метод является основным при расчете нелинейных цепей как в переходном, так и в установившемся режиме.

6. Расчет переходного процесса на ЭВМ по стандартной программе

Система нелинейных дифференциальных уравнений, составленная для схемы цепи по законам Кирхгофа и дополненная уравнениями аппроксимации физических характеристик нелинейных элементов, может быть решена численным методом на ЭВМ по стандартной программе. Применение данного метода показано ниже на конкретном примере.

а) Задана схема цепи (рис. 103) и параметры отдельных элементов в единицах измерения SI. Нелинейная вебер-амперная характеристика катушки индуктивности аппроксимирована уравнением i = a·sinh(b·ψ).

137

б) Для схемы составляется система уравнений Кирхгофа в дифференциальной форме и дополняется уравнением аппроксимации ВбАХ. Система дифференциальных уравнений приводится к форме Коши.

в) Система дифференциальных уравнений решается численным методом по одной из стандартных программ MathCAD (rkfixed или Rkadapt). Массивы значений для искомых функций, получаемые в результате решения, методом линейной интерполяции превращают в соответствующие функции времени.

F rkfixed (N 0 0.1 5000 D)

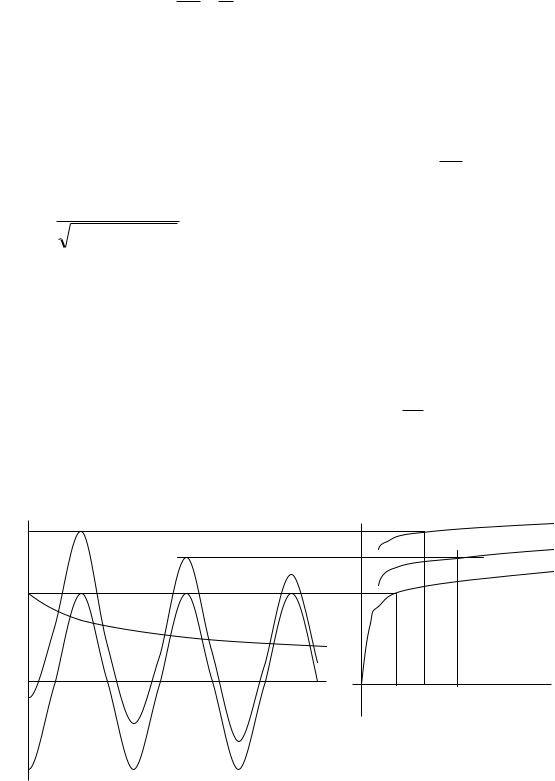
г) Производится математическая обработка результатов расчета. Строится графическая диаграмма функции тока i(t), определяются параметры переходного процесса (рис. 104).

138

t

Рис. 104

К достоинствам численнного метода следует отнести следующее:

1)Сравнительно невысокая трудоемкость метода, так как все расчеты выполняются ЭВМ по встроенным программам MathCAD.

2)Универсальность метода. Метод пригоден для расчета любых нелинейных цепей с разными данными.

3)Высокая точность вычислений, которая обеспечивается методом Рунге-Кутта 4-го порядка.

4)Метод позволяют проводить анализ работы схемы как в переходном, так и в установившемся режимах при изменении параметров отдельных элементов.

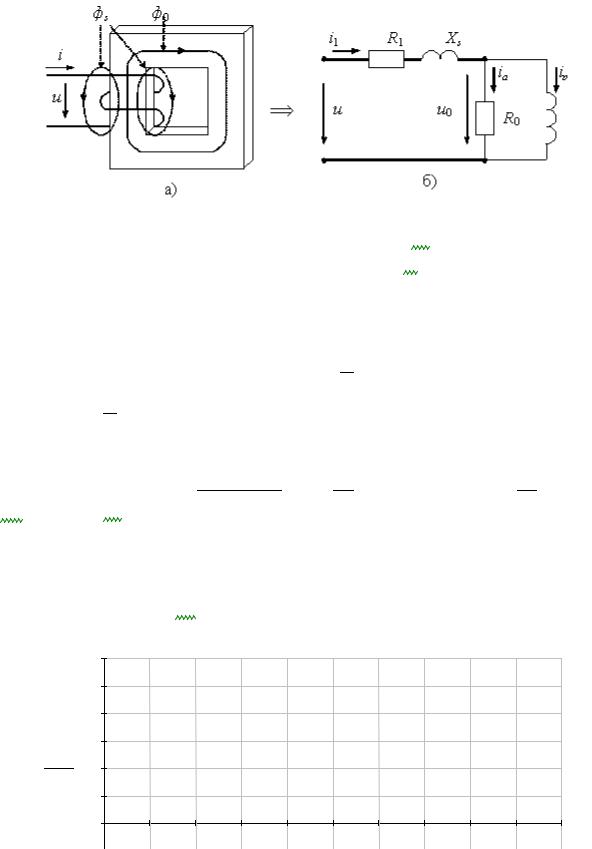
7.Расчет переходного процесса в трансформаторе при его включении в режиме холостого хода

Ниже приведен конкретный пример расчета переходного процесса в трансформаторе при его включении в режиме холостого хода на ЭВМ по стандартной программе. В качестве расчетной схемы принята стандартная схема замещения трансформатора.

а) Заданы схема замещения трансформатора (рис. 105) и параметры элементов

139

б) Система дифференциальных уравнений и ее решение

t

Рис. 106. Графическая диаграмма функции тока i(t).

140