2

7. Электростатическое поле и емкость цилиндрического провода, расположенного над проводящей плоскостью (землей)

Пусть требуется рассчитать электростатическое поле и емкость цилиндрического провода, расположенного над проводящей плоскостью (землей). Заданны радиус провода R, высота подвески h (радиус R соизмерим с высотой h). К проводу приложено постоянное напряжение U (рис.

117).

h

–

O2

Рис. 117

Согласно второму следствию из теоремы единственности заменим проводящую среду диэлектриком, а поверхностные заряды провода и земли двумя разноименно заряженными осями + и – так, чтобы остались неизменными прежние граничные условия: 1) поверхность земли должна быть эквипотенциальной с потенциалом 0 = 0, 2) поверхность провода должна быть эквипотенциальной с потенциалом 1 = U. Чтобы выполнить эти условия, электрические оси + и – должны быть смещены относительно геометрических осей на некоторое расстояние s a.

Положение электрических осей определяется из теоремы Аполония:

(s a)(s a) R2

s h

161

Таким образом, электростатическое поле, создаваемое двумя проводами с поверхностными зарядами σ, будет эквивалентным полю, которое создается двумя разноименно заряженными осями + и – , и для его расчета можно применить полученные ранее формулы:

где (s – a) – смещение электрической оси провода относительно геометрической.

Из полученного выражения вытекают расчетные формулы:

Если высота подвеса провода намного больше его радиуса, то смещением электрических осей можно пренебречь (s a 0) и считать, что электрические оси проводов совпадают с геометрическими. В этом случае расчетные формулы будут иметь вид:

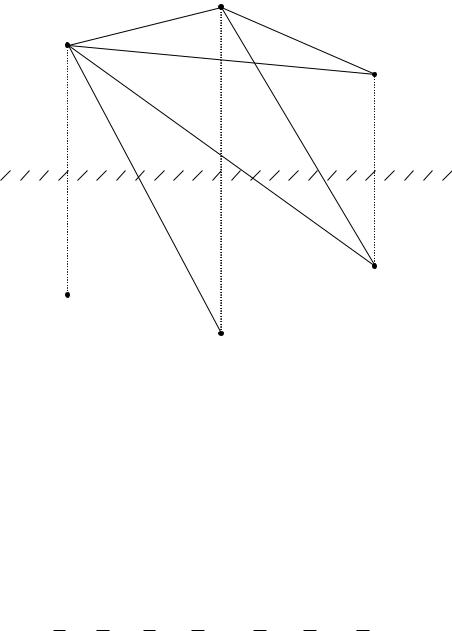
8. Поле многопроводной линии. Метод зеркальных отображений

Заданы n длинных проводов, расположенных параллельно проводя-

162

– 3, – 3

– 1, – 1

– 2, – 2

Рис. 118

На основании второго следствия из теоремы единственности заменим

ды земли – системой зеркальных зарядов проводов с противоположными знаками. Смещением электрических осей пренебрегаем, так как по усло-

вию h >>R.

Расчет параметров поля в произвольной точке n может быть выполнен по методу наложения, то есть результирующие параметры поля могут быть найдены как суммы соответствующих составляющих от независимого действия осевых зарядов самих проводов и их зеркальных отображений:

Аналогично для каждого провода:

163

Здесь обозначены:

тенциальные коэффициенты.

Потенциальные коэффициенты определяются через геометрические размеры, они всегда положительны, имеют физическую размерность [1/Ф].

могут быть определены из совместного решения системы потенциальных уравнений (первой группы формул Максвелла):

отрицательны.

На практике более удобно пользоваться формулами Максвелла третьей группы с частичными ёмкостями:

соответствующими элементами схемы (рис. 119).

164

Частичные емкости определяются через емкостные коэффициенты второй группы формул.

Метод расчета полей многопроводных линий, основанный на применении второго следствия из теоремы единственности, получил название метода зеркальных отображений.

Рассмотрим применение данного метода к расчету рабочей емкости двухпроводной линии, расположенной над поверхностью земли. Если провода линии питаются от незаземленного источника, то можно принять для

Откуда следует формула рабочей емкости линии с учетом влияния земли:

Если линия расположена достаточно высоко над поверхностью земли (h >> d), то D 2h и уравнение для рабочей емкости превращается в урав-

165

нии без учета влияния земли.

9. Электрическое поле трехфазной линии электропередачи

Геометрические размеры в поперечном сечении линии электропередачи несравнимо малы по сравнению с длиной электромагнитной волны на

речном сечении линии могут не учитываться, а полученные ранее соотношения для многопроводной линии в статическом режиме с большой степенью точности могут быть применены к расчету поля линий электропередач переменного тока на промышленной частоте f = 50 Гц. Изменяющиеся по синусоидальному закону потенциалы проводов ЛЭП по отношению к параметрам поля можно считать квазистатическими или медленно изменяющимся, и расчет параметров поля для каждого момента времени можно выполнять по полученным ранее уравнениям электростатики.

При синусоидальном законе изменения потенциалов и зарядов проводов формулы Максвелла можно записать в комплексной форме:

Потенциалы проводов ЛЭП равны соответствующим фазным напряжениям и определяются генератором.

Для трехфазных ЛЭП применяются различные варианты расположения проводов в пространстве. На рис. 120 приведены два из них: а) по вершинам равностороннего треугольника, б) в одной плоскости, параллельной поверхности земли. В первом варианте равны расстояния между

ким образом, в воздушных трехфазных ЛЭП не может быть достигнута полная симметрия проводов в пространстве. Потенциальные коэффициен-

будут несимметричными в формулах первой группы формул Максвелла. Несимметрия потенциальных коэффициентов вызовет несимметрию заря-

дов проводов A , B , C и соответствующую несимметрию зарядных токов

166

линии I A , I B , IC в режиме холостого хода. Полная симметрия проводов в пространстве достигается только в кабельных линиях.

B

Рис. 120

Для устранения несимметрии фаз воздушных линий электропередачи через равные расстояния (обычно через 1/3 длины) производят круговую перестановку или транспозицию проводов (рис. 121). При наличии транспозиции усредненные значения параметров линии получаются одинаковыми для всех фаз, при этом несимметрия между началом и концом линии устраняется.

C

A B

B

B C

A

C A

Рис. 121

Средние значения потенциалов коэффициентов для транспонированной линии:

,

167

рические значения расстояний.

Потенциальное уравнение для провода фазы А транспонированной линии получит вид:

Если длина линии равна l, то эквивалентная емкость фазы на землю составит Сф = С0l, а ток холостого хода линии будет равен I0 = Uф/XC =

= Uф C.

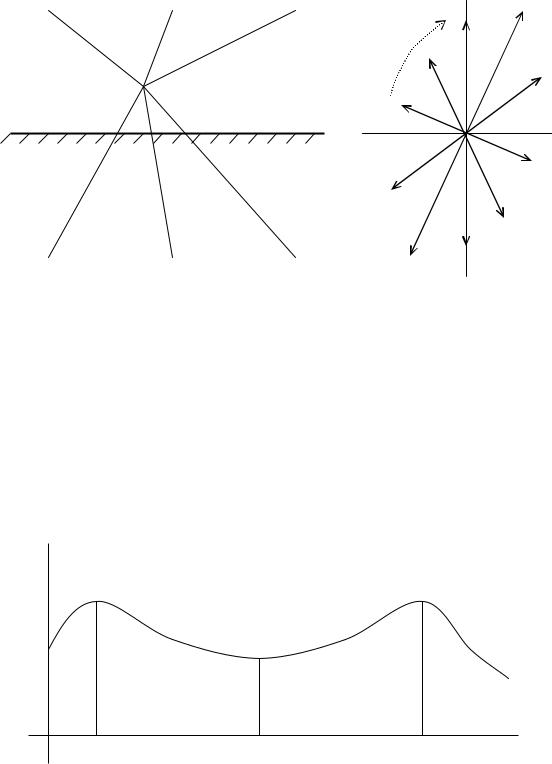
Исследуем, как будет изменяться напряженность электрического поля в произвольной точке n в поперечном сечении линии (рис. 122, а) в интервале времени одного периода.

En EnA EnB EnC E nA E nB E nC .

Расчеты показывают, что в интервале времени одного периода вектор E будет изменяться по модулю и по направлению и за один период опишет эллипсовидную фигуру (рис. 122, б). Таким образом, электрическое поле в поперечном сечении ЛЭП является вращающимся, но не круговым, эллиптическим по форме. Максимальное значение этого вектора Emax соответствует большой полуоси эллипса.

168

x

На рис. 123 представлена графическая диаграмма Emax = f(x) при y = 1м = const для ЛЭП с расположением проводов в плоскости, параллельной по-

верхности земли. Анализ диаграммы показывает, что абсолютный максимум этой функции имеет место с внешней стороны крайних проводов ЛЭП, а под средней фазой напряженность поля меньше, чем под крайними фазами (рис. 123).

Emax

A B C

Emax(abs)

x

Рис. 123

169

Т2. Электрическое поле постоянного тока

1.Законы электрического поля в интегральной

идифференциальной формах

Под электрическим током проводимости i понимается движение свободных зарядов в проводящей среде γ под действием сил электрического

ром плотности: