
- •Н.А. Ююкин
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •1.3.1. Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •1.4. Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2).4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z– преобразования
- •1.6.2. Обратное преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. СвойстваZ-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7.Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Теория автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики.
- •2.6. Модификации конечных автоматов
- •2.6.1. Не полностью описанные (частичные) автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автомата
- •2.7. Процедура минимизации не полностью описанного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний.
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •1. Элементы комбинаторики 7
- •2. Теория автоматов 58
- •3. Введение в нечеткую математику 106
2.7.3. Построение минимального автомата
Совместным
классом ![]() называется множества внутренних
состояний таких , что
называется множества внутренних
состояний таких , что![]() для всех
для всех![]() . Максимальным совместимым классом
. Максимальным совместимым классом![]() называется совместимый класс, не
содержащийся в качестве собственного
подмножества в другом совместимом
классе. Полное множество максимальных
совместимых классов есть список самых
больших подмножеств состояний, каждое
можно склеить в одно состояние. В нашем
случае максимально совместимы классы
(1,2), (1,4),(2,3) и (3,4,5,).
называется совместимый класс, не
содержащийся в качестве собственного
подмножества в другом совместимом
классе. Полное множество максимальных
совместимых классов есть список самых
больших подмножеств состояний, каждое
можно склеить в одно состояние. В нашем
случае максимально совместимы классы
(1,2), (1,4),(2,3) и (3,4,5,).
Определение.Некоторое множество совместимых классов
называется согласованным, если для
любого класса![]() из этого множества и любых его элементов
из этого множества и любых его элементов![]() внутренние состояния
внутренние состояния![]() принадлежат подходящему совместимому
классу
принадлежат подходящему совместимому
классу![]() для любого символа
для любого символа![]() .
.
Определение. Некоторое множество совместимых классов называется замкнутым, если всякое внутренне состояние автомата принадлежит хотя бы одному из этих классов
Теорема.
Пусть задано замкнутое согласованное
множество совместимых классов для
автоматаM,тогда существует
автомат![]() ,
покрывающий автомат М, состояния которого
получаются склеиванием всех состояний
М, содержащихся в одном совместимом из
данного множества.
,
покрывающий автомат М, состояния которого
получаются склеиванием всех состояний
М, содержащихся в одном совместимом из
данного множества.
Если
исходное замкнутое согласованное
множество содержит наименьшее число
совместимых классов, то автомат ![]() ,
покрывающий автомат М, и полученный
склеиванием всех состояний каждого
класса в одно состояние, будет минимальным.
,
покрывающий автомат М, и полученный
склеиванием всех состояний каждого
класса в одно состояние, будет минимальным.
Рассмотрим
автомат, анализируемый ранее. Одно из
возможных предложений состоит в разбиении
на классы эквивалентности ![]() и
и![]() ,
которое привело бы к автомату с двумя
состояниями. Однако
,
которое привело бы к автомату с двумя
состояниями. Однако![]() ,
это значит, что данное предложение не
годится, поскольку указанное разбиение
не согласованно. Никакая другая пара
совместимых классов не покрывает всё
множество состояний. Поэтому следует
рассмотреть разбиение на 3 класса. Такое
согласованное разбиение из трех классов
существует.
,
это значит, что данное предложение не
годится, поскольку указанное разбиение
не согласованно. Никакая другая пара
совместимых классов не покрывает всё
множество состояний. Поэтому следует
рассмотреть разбиение на 3 класса. Такое
согласованное разбиение из трех классов
существует.![]() Соответствующий
минимальный автомат.
Соответствующий
минимальный автомат.
Рассмотрим другой пример таблицы состояний автомата
|
Текущее состояние |
Следующее состояние |
Выход | ||||||
|
|
|
|
|
|
|
|
| |
|
1 |
2 |
1 |
- |
- |
0 |
- |
- |
1 |
|
2 |
1 |
1 |
- |
2 |
- |
0 |
- |
- |
|
3 |
1 |
4 |
3 |
- |
1 |
0 |
0 |
1 |
|
4 |
1 |
4 |
2 |
2 |
0 |
- |
0 |
- |
|
5 |
2 |
- |
2 |
- |
- |
0 |
- |
1 |
![]() все
остальные
все
остальные
Составим таблицу совместимости
|
|
|
|
|
|
|
(1,2) |
- |
- |
- |
- |
|
(1,4) |
(1,2) |
(1,4) |
- |
- |
|
(1,5) |
- |
- |
- |
- |
|
(2,3) |
(1,2) |
(1,4) |
- |
- |
|
(2,4) |
(1,2) |
(1,4) |
- |
- |
|
(2,5) |
- |
- |
- |
- |
|
(3,5) |
(1,2) |
- |
(2,3) |
- |
|
(4,5) |
(1,2) |
- |
- |
- |
Максимально совместимыми классами являются {1,2,4,5} и {3}
Это разбиение является согласованным, следовательно, соответствующий автомат выглядит следующим образом
|
Текущее состояние |
Следующее состояние |
Выход | ||||||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
- |
1 |
0 |
0 |
1 |
3. Введение в нечеткую математику
3.1. Нечёткие множества
Пусть U-универсальное
множество,А– некоторое подмножество
множестваU![]() .
Тот факт, что элементхмножествоUпринадлежит
подмножествуАобозначается в виде
.
Тот факт, что элементхмножествоUпринадлежит
подмножествуАобозначается в виде![]() .Для
выражения этой принадлежности можно
воспользоваться понятием характеристической
функции
.Для
выражения этой принадлежности можно
воспользоваться понятием характеристической
функции
![]()
В данном случае
характеристическая функция
![]() принимает
только два значения 0 и 1.
принимает
только два значения 0 и 1.
Нечетким множеством А множества Uназываются множество упорядоченных пар
![]()
Где
![]() -
функция принадлежности, принимающая
свои значения извполныеупорядоченных.
-
функция принадлежности, принимающая
свои значения извполныеупорядоченных.
Если
![]() ,
то нечеткое множество рассматривается,
как обычное множество, являющиеся
подмножеством универсального множестваU.
,
то нечеткое множество рассматривается,
как обычное множество, являющиеся
подмножеством универсального множестваU.
Функция принадлежности
может задаваться графически. Для этого
в прямоугольной системе координат по
оси ординат откладывается значение
![]() и по оси абсцисс элементы множестваU.
и по оси абсцисс элементы множестваU.
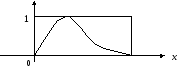
В случае конечного множества используется следующая запись:
![]()
Знак + обозначает объединение элементов.
Например, запись
![]()
Означает, что элемент упивергуни
1 принадлежит А со степенью 0
2 принадлежит А со степенью 0.1
2 принадлежит А со степенью 1.0
Множество пусто,
т.е.
![]()
![]() ,
если
,
если![]() .
Два множества А и Вравны, т.е. А=В если
.
Два множества А и Вравны, т.е. А=В если![]() .
.
Множество А
включается вВ, т.е. ![]() если
если![]() .
.
Множество![]() естьдополнениеА, если
естьдополнениеА, если![]() .
.
Пересечениемножеств А и В, если![]() .
.
Объединение![]() .
.
Пример
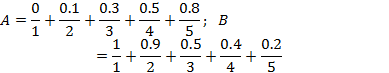
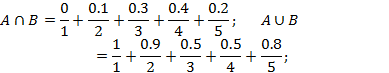
Разностьнечетких множеств![]() .
.
Пример
![]()
Симметричная разностьнечетких множеств
![]()
Прямое произведениенечетких множеств
![]()
Пример
![]()
![]()
|
|
B | ||
|
1 |
2 | ||
|
A |
1 |
0.5 |
1 |
|
2 |
0.5 |
0.7 | |
Операция
концентрации![]() возводит
функцию принадлежности в квадрат.
возводит
функцию принадлежности в квадрат.
Операция
деконцентрации![]() извлекает
квадратный корень из функции принадлежности.
извлекает
квадратный корень из функции принадлежности.
