1.8. Матрицы Адамара

1.8.1. Определение матрицы Адамара и ее свойства

Матрица H=(h_ij), i,j=1,2,_,n, h_ij=1 называется матрицей Адамара, если она удовлетворяет равенству

HH^T= nI_n (1)

где I_n – единичная матрица nn и - транспонированная матрица H.

Матричное равенство (1) может быть записано в виде:

= (2)

Следовательно, если H₁,H₂,..,H_n – строки матрицы H, то эти строки, как векторы, удовлетворяют условию ортогональности

() = (3)

где () - скалярное произведение векторов и .

Из матричного равенства (1) следует , что

det(HH^T) = (detH)² = det(nI_n) = nⁿ

и, следовательно, |detH| = n^n/2.

А это означает что detH 0 и, следовательно, матрица H – невырожденная. Это, в свою очередь, говорит о том, что для матрицы H существует обратная ей матрица H^-1. Запишем следующую систему равенств.

H^TH =H^-1 HH^TH =H^-1(nI_n)H = nI_n = HH^T

Следовательно, матрица H удовлетворяет условию нормальности, то есть

H^TH = HH^T

1.8.2. Эквивалентные преобразования матриц Адамара

Перестановки строк или столбцов, а так же умножение строк или столбцов на (-1) переводит матрицу Адамара H в эквивалентную матрицу Адамара H₁. Действительно, перестановка строк матрицы H, в соответствии, с (3) сохраняет все скалярные произведения строк. Перестановка столбцов связана с изменением порядка слагаемых в формуле (2). Аналогичным образом не изменяются в соответствии с (2) скалярные произведения строк или столбцов при умножении на (-1). С помощью эквивалентных преобразований матрицу Адамара можно привести к нормализованному виду , в котором первая строка и первый столбец состоят из положительных единиц. Нормализованными матрицами Адамара 1-го и 2-го порядков являются

H₁ = (1), H₂ = (4)

Рассмотрим нормализованную матрицу Адамара порядка n. Для этого построим матрицу , образованную первыми тремя строками матрицы . Столбцы матрицы могут быть следующих четырех видов

, , ,

Обозначим через x, y, z и w – число столбцов матрицы каждого из 4 видов соответственно. Тогда из условия ортогональности строк (3) получаем систему уравнений

x + t + z + w = n (1x1)

x – y + z – w = 0 (1x2)

x + y – z – w = 0 (1x3)

x – y – z + w = 0 (2x3)

Данная система уравнений имеет единственное решение

x = y = z = w =

Таким образом при n имеем n = 4, где - натуральное число.

Например, случай n=3 исключается, так как два вектора размерности 3 с координатами не могут быть ортогональными.

Таким образом, матрицы Адамара могут существовать для всех порядков, кратных четырем. Для их построения используются разнообразные методы. Так, для n матрицы Адамара были построены для всех порядков, кратных 4 за исключением n = 116, 156, 188.

1.8.3. Построение матриц Адамара

Рассмотрим способ построения матриц Адамара исходя из матриц Адамара меньшего порядка.

Кронекеровым произведением матрицы A = (a_ij) i,j=1,2,..,m на матрицу B = (b_ij) i,j = 1,2,..,n называется (mn) матрица вида = (a_ijB), i,j=1,2,..,m.

Имеют место следующие свойства кронекерова произведения матриц (исходя из определения):

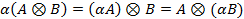1. , где - скаляр.

2. .

3. .

4. .

5. .

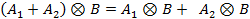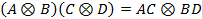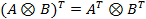Здесь A,A₁,A₂,C и B,B₁,B₂,D - матрицы порядков m и n соответственно.

Теорема. Кронекерово произведение матриц Адамара порядков m и n есть матрица Адамара порядка mn.

Доказательство. Пусть H_m и H_n - матрицы Адамара порядков m и n соответственно. Тогда для их кронекерова произведения имеем

=.

Отсюда в соответствии с (1) следует, что H_mn есть матрица Адамара порядка mn.

Следствие. Для любого матрица Адамара существует

Действительно при матрица

(d раз), где H₂ - матрица вида (4). Согласно теореме она есть матрица Адамара.