
Пособие ДМ2
.pdf
Н.А. Ююкин
ДИСКРЕТНАЯ МАТЕМАТИКА
ЧАСТЬ 2
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ КОНЕЧНЫХ АВТОМАТОВ
Учебное пособие
A
B0
B
B |
* |
|
0 |
||
|
||
B |
* |
|
1 |
||
|
B1 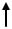
Воронеж 2011
ГОУВПО «Воронежский государственный технический университет»
Н.А. Ююкин
ДИСКРЕТНАЯ МАТЕМАТИКА
ЧАСТЬ 2
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ КОНЕЧНЫХ АВТОМАТОВ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2011
УДК 519.17
Ююкин Н.А. Дискретная математика. Ч. 2: Элементы комбинаторики и теории конечных автоматов: учеб. пособие /Н.А. Ююкин/ Воронеж: ГОУВПО «Воронежский государственный технический университет», 2011. 98 с.
В учебном пособии рассматриваются краткие теоретические сведения об основных комбинаторных конфигурациях и задачах по их перечислению; о рекуррентных уравнениях и методах их решения. В теории конечных автоматов даётся их формальное определение, классификация,различные варианты представления, тестирование и применение. Кроме того, в пособии представлен материал по нечеткой математике.
Учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 090100 «Информационная безопасность», специальностям 090102 «Компьютерная безопасность», 090105 «Комплексное обеспечение информационной безопасности автоматизированных систем», 090106 «Информационная безопасность телекоммуникационных систем», дисциплины «Дискретная математика».
Учебное пособие подготовлено в электронном виде в текстовом редакторе MSWORD и содержится в файле «Теория автоматов» Ил. 58. Библиогр.: 8 назв.
Научный редактор д-р физ.-мат. наук, проф. И.Л. Батаро-
нов
Рецензенты: кафедра высшей математики Воронежского института МВД России (начальник кафедры д-р физ.- мат. наук, проф. В.В. Меньших); канд. физ.-мат. наук, доц. С.П. Майорова
©Ююкин Н.А., 2010
©Оформление. ГОУВПО
«Воронежский государственныйтехнический университет»,
2011
ВВЕДЕНИЕ
Данное пособие может быть использовано в курсе “Дискретная математика” студентами ВГТУ, обучающимися по специальностям:
090102 – Компьютерная безопасность;
090105 – Комплексное обеспечение информационной безопасности автоматизированных систем;
090106 - Информационная безопасность телекоммуникационных систем.
Дисциплина “Дискретная математика” обеспечивает приобретение знаний и умений в соответствии с Государственным, общеобразовательным стандартом, и при этом содействует фундаментализации образования, формированию мировоззрения и развитию логического мышления.
Дискретная математика является эффективным аппаратом формализации современных инженерных задач, связанных с дискретными объектами. Она используется при проектировании интегральных схем и схем управления, исследовании автоматов и логических цепей, в системном анализе, автоматизированном управлении производством, при разработке вычислительных и информационных сетей, в схемотехническом и конструкторско-топологическом проектировании и т.д.
Вучебном пособии излагаются основы, базовые методы
иалгоритмы теории: принцип включения-исключения; рекуррентные соотношения и производящие функции; трансверсали; латинские прямоугольники и квадраты; комбинаторные конфигурации, блок-схемы; конечные проективные плоскости; ортогональные латинские квадраты; матрицы Адамара. Здесь представлены конечные автоматы; автоматные базисы и проблема полноты; эквивалентность в автоматах; автоматные языки; понятие формальной грамматики; эксперименты с автоматами; тестирование автоматов; веро-
ятностные автоматы, а также вырабатываются практические навыки по использованию вышеприведенных понятий.
Целью курса является формирование у студентов теоретических знаний, практических умений и навыков в области моделирования процессов и явлений в естествознании и технике, с возможностью употребления математических символов для выражения количественных и качественных отношений объектов, необходимых для выполнения служебной деятельности в области защиты информации на высоком профессиональном уровне.
Достижению данной цели служат следующие задачи:
изучить максимально широкий круг понятий теории;
получить навыки решения учебных и практических задач;
овладеть методами оптимизации;
выработать навыки постановки и решения информационных задач, моделирования и анализа информации с помощью комбинаторных методов и конечных автоматов.
Дисциплина “Дискретная математика” относится к числу
прикладных математических дисциплин. Она основывается на знаниях, приобретенных студентами при изучении дисциплин “Алгебра” и “Математическая логика и теория алгоритмов”. Знания и навыки, полученные при изучении дисциплины “Дискретная математика” используются при изучении обще профессиональных и специальных дисциплин.
1.ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
1.1.Простейшие комбинаторные конфигурации
Комбинаторика – раздел математики, связанный с решением задач выбора и размещения элементов конечного множества в соответствии с заданными правилами.
Каждое правило определяет способ построения некоторой конструкции из элементов исходного множества. Полученные конструкции называются комбинаторными конфигурациями.
Цель комбинаторного анализа заключается в изучении комбинаторных конфигураций, алгоритмов их построения, а также решении задач по их перечислению.
1.1.1. Основные правила комбинаторики
Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.
Правило суммы. Пусть A, B – конечные множества, |A| = n, |B| = m.
| |
| |
| |
|, |
следовательно |
|
|
|
| |
| |
|
. |
Комбинированная интерпретация.
Если некоторый объект A можно выбрать n способами, а другой объект B можно выбрать m способами, то выбор "либо A, либо B" можно осуществить n+m способами.
|
Правило произведения. Если мощность |A| = n, |B| = m, |
|
то | |
| |
. |
Комбинаторная интерпретация.
Если объект A можно выбрать n способами, а после каждого такого выбора другой объект B можно выбрать (независимо от выбора объекта A) m способами, то пары объ-
ектов A и B можно выбрать |
m n |
способами. |
|
|
|
|
|||||||
Пусть |
A a1 , a2 ,..., an , |
B b1 ,b2 ,...,bm |
и |А| - число |
||||||||||
элементов множества A. Составим декартово произведение |
|||||||||||||
A B множеств A и B, т.е. множество пар ai ,bi |
. |
|
|
|
|||||||||
|
|
{(a |
|
,b ), |
(a |
,b ), |
|
(a |
,b |
), |
|||
|
|
|
1 |
1 |
|
1 |
2 |
|
|
1 |
m |
|
|
a A,b B : A B |
(a |
|
,b ), |
(a |
|
,b ), |
|
(a |
|
,b |
), |
||
|
2 |
|
1 |
|
2 |
2 |
|
|
2 |
m |
|
||
|
|
|
|
|
|
|
|
||||||
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(a |
n |
,b ), |
(a |
n |
,b ), |
|
(a |
n |
,b |
)} |
|
|
|
|
|
1 |
|
2 |
|
|
m |
|
|||
Тогда правило произведения записывается следующим |
|||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A B | | A | | B | |
|
|
|
|
|
||||||
Пример. Сколько всего существует двузначных чисел? Решение. Поскольку в двузначном числе цифра, обозна-
чающая число десятков, должна быть отлична от нуля, то A = {1, 2, ..., 9}, B = {0, 1, 2, ..., 9} и
,
| A B | | A | | B | 90.
1.1.2. Выборки элементов без повторений
Простейшими комбинаторными конфигурациями являются перестановки, размещения и сочетания.
Перестановки. |
|
Пусть |
. Перестановкой элементов |
множества M называется любой упорядоченный набор эле- |
|
ментов |
, состоящий из n различных элемен- |
товмножества M. |
|

Перестановки отличаются друг от друга порядком следования элементов.
Теорема. Число всех перестановок равно n!
Доказательство. На первом месте можно разместить n элементов, на втором – любой из оставшихся (n-1) элементов и т.д. Для последнего места остается 1 элемент. В силу правила произведения имеем:
.
Пример. Сколькими способами можно разместить 5 студентов при наличии 5 мест.
.
Размещения.
Пусть множество M состоит из n элементов. Размещением (упорядоченной выборкой) из n элементов по m элементов называется любой упорядоченный набор элементов , состоящий из m различных элементов мно-
жества M.
Теорема. Число размещений n элементов по m элементов обозначается . . Справедлива формула:
Доказательство. Размещение M элементов множества Mможно представить, как заполнение некоторых m позиций элементами множества M. При этом первую позицию можно заполнить nспособами, вторую позицию (n-1) способами. Последнюю позицию можно заполнить (n-m+1) способами.

Пример. Из 10 книг производным образом берутся 3 книги и ставятся на полку. Сколько существует способов такой расстановки книг.
.
Заметим, что размещение из n элементов по n элементам представляет собой перестановку, т.е.:
Сочетания.
Сочетанием (неупорядоченной выборкой) из n элементов по m, где m n , называется неупорядоченное подмножество множества M, состоящее из n различных элементов.
Теорема. Число сочетаний из n элементов по m обозначается как и определяется по формуле:
Доказательство. Если объединить размещения из n элементов по m, которые состоят из одних и тех же элементов (то есть не учитывать порядка расположения элементов), то получим сочетание из n элементов по m. Так как для каждого такого сочетания можно получить n! размещений. Тогда
и, следовательно:
.
1.1.3. Выборки элементов с повторениями
Размещением (упорядоченной выборкой) с повторениями из n элементов по m называется любой упорядоченный набор , элементы которого могут повторяться. Поскольку в упорядоченном наборе может находиться любой из n элементов, то число размещений с повторениями (обо-
значение такого числа ̅̅̅̅) равно nm. Таким образом:
̅̅̅̅

Пример. Из чисел 1, 2, 3, 4 составляются трехзначные
числа. Сколько чисел можно получить таким образом.
̅̅̅ .
Сочетанием (неупорядоченной выборкой) с повторениями из n элементов по m элементов называется множество, состоящее из элементов, выбранных m раз из множества M. При этом допускается выбирать элемент повторно.
Число сочетаний с повторениями из n элементов по m обозначается ̅̅̅̅.
̅̅̅̅
Пример. Сколько существует различных результатов бросания двух одинаковых кубиков.
̅̅̅̅
Выбор элементов |
Упорядоченная |
Неупорядоченная |
|
|
|
Без повторений |
|
|
|
|
|
С повторениями |
̅̅̅̅ |
̅̅̅̅ |
|
|
|
1.2. Латинские прямоугольники, конечные проективные плоскости и блок-схемы
1.2.1. Латинские прямоугольники
Пусть дано множество S из n элементов. Латинский прямоугольник, основанный на множестве S, есть прямо-
угольная |
таблица. |
|
( ) |
Каждая строка – упорядоченная выборка элементов множества S длины s, каждый столбец – упорядоченная выборка элементов множества S длины r, причем r n , s n .
