
Пособие ДМ2
.pdfАкцептором с конечным числом состояний (конечным акцептором, анализатором) называется пятерка , где:
-конечное множество входных символов,
-конечное множество внутренних состояний,
φ - функция из |
в , |
-начальное состояние
-множество принимающих состояний.
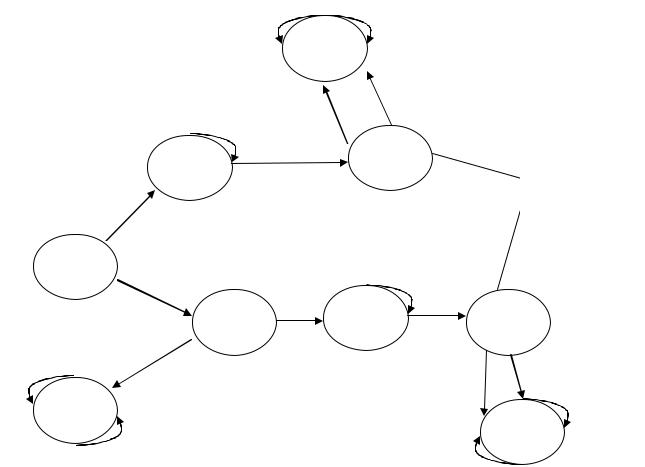
Входные символы линейно упорядочены, так как они напечатаны на входной ленте, и последовательно считываются читающей головкой. Пример конечного акцептора, заданного с помощью графа.
0 |
1 |
|
|
|
1 |
|
|
0 |
|
|
|
Принимающее |
|
0 |
|
|
|
|
|
||
|
1 |
|
конечное значе- |
|
|
ние |
|
|
|
|
|
|
|
={ |
|
0
|
|
|
1 |
|
|
1 |
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
1 |
1 |
|
1 |
0 |
0
0
1
Данный акцептор принимает, в частности следующие строки как 001, 0001, 100, 1010, 10110.
Рассмотрим класс грамматики, порождающих в точности такие множества строк, которые принимаются некоторым конечным акцептором.
Определение. Автоматной грамматикой называется четверка[ ], где
-конечное множество входных символов,
-конечное множество терминальных символов,
-конечное множество правил порождения вида
е
- отмеченный начальный символ.
Небольшие конечные акцепторы, а также автоматные грамматики, удобно изобразить с помощью диаграмм состояний. Для составления диаграммы состояний автоматной грамматики - следует произвести следующие действия:
Шаг |
1. |
Каждому |
нетерминальному |
символу из |
|||
постaвить в соответствие вершину графа. |
|
|
|||||
Шаг 2. Каждому правилу |
|
поставить в соответ- |
|||||
ствие |
дугу от вершины |
к |
вершине, |
помеченную |
|||
символом. |
|
|
|
|
|
||
Шаг 3. Каждому правилу |
|
поставить в соответ- |
|||||
ствие дугу от вершины к |
в й вершине, |
с пометкой |
|||||
ПРИНЯТЬ. |
|
|
|
|
|
||
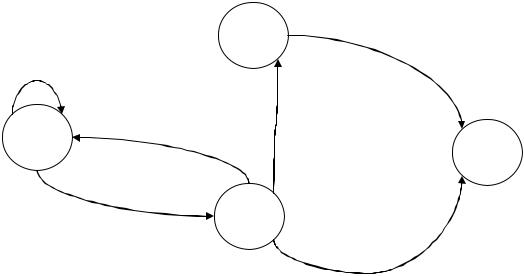
Пример. |
На рисунке |
показана |
диаграмма |
состояний |
|||
(помеченный ориентированный граф), отвечающая автоматной грамматике Gс правилами.
|
|
|
X |
|
с |
|
с |
|
|
|
|
A |
|
с |
b |
|
|
При
нять
Y
b
с
Для автоматных грамматик справедлив ряд утверждений (теорем):
1.Последовательность меток дуг вдоль любого конечного пути, начинающегося из вершины А. На диаграмме грамматикиG, является строкой, порождаемойG, и, наоборот, все порождаемые строки отвечают некоторым путям.
2.Для любой автоматной грамматики существует конечный акцептор, принимающий в точности те строки, которые порождает грамматика.
3.Для любого конечного акцептора существует автоматная грамматика, порождающая в точности те строки, которые принимаются этим акцептором.
4.Существуют контекстно-свободные языки, не являющиеся автоматными языками.
2.6. Модификации конечных автоматов
Существуют многочисленные модификации конечных автоматов. С одной из них мы уже знакомились – это машины Тьюринга. Рассмотрим модификации, связанные с обобщенными переходами и выходной функцией. Для них допускается произвольные отношения случайной функции и т.п. К этим отношениям относятся частичные, недетерминированные и вероятные автоматы.
2.6.1. Не полностью описанные (частичные) автоматы
В определении конечного автомата (A, S, B, , ) предполагается, что функции и всюду определены.
Однако на практике, встречаются случаи, когда они лишь частично определены. Это связано с тем, что сложные системы проектируются по частям и поэтому может оказаться, что некоторые входящие строки либо вообще не встречаются, либо встречаются в случаях, когда выход нас не интересует. Это приводит к тому, что некоторые позиции в таблицах состояний (или ребра в диаграммах состояний) отсутствуют. Также позиции называются безразличными, т.к. нас не интересуют их содержания. В таблицах состояний они обозначается прочерками.
Например, в таблице
Текущее со- |
Следующее |
состоя- |
Выход |
|
|
стояние |
ние |
|
|
|
|
|
0 |
|
1 |
0 |
1 |
S0 |
S1 |
|
S2 |
0 |
1 |
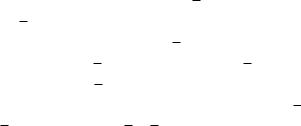
S1 |
- |
S1 |
1 |
0 |
S2 |
S0 |
S1 |
- |
1 |
|
|
|
|
|
Т.е. в данном случае безразлично состояние автомата начавшего работу из состояния S, и считавшего входной символ 0, так же безразличен выход автомата, находя-
щегося в состоянии
S |
2 |
|
и считавшего символ 0.
Для представления способа минимизации не полностью описанных автоматов используются следующие определения.
|
Опр.1. |
Входная |
последовательность |
|
|
|
|
a a0a1a2 ...an 1 |
называется |
допустимой для автомата |
|
находившегося в начальном состоянии S j , если функ-
ция перехода |
|
определена для всех элементов после- |
довательности, кроме возможно последнего. т.е, допустимая входная строка автомата с начальным состояни-
ем |
S |
j однозначно определяет строку внутренних состо- |
|
яний, за исключением последнего состояния, которое может быть неопределенным (безразличным).
|
Опр.2. Выходная строка |
b покрывает выходную |
||||||||
строку |
b ' (в которой могут быть неопределенные сим- |
|||||||||
волы), |
если любой символ из b ' |
равен соответствующе- |
||||||||
му символу b |
i |
|
|
|
|
|
0 1 |
2 |
011 |
|
|
из b . Например, строка b b b b |
|
||||||||
покрывает строку b ' b |
0 |
1 |
2 |
' 11; строка 010 покры- |
||||||
|
'b 'b |
|
||||||||
вает -10, строка 110 покрывает 110 и -10. Если b покры-
вает
b
' , то пишут, что |
|
Опр.3. Если |
|
|
|
b |
|
r |
(s |
k |
|
b'
,a
.
) (s |
, a), a |
|
r |
j |
|
, для допу-
стимых
s |
s |
k |
j . |
s j
, то говорят, что sk
покрывает
s j
, и пишут
Опр.4. Автомат M покрывает M , если s j автомата M существует такое состояние sk автомата M ,
что |
r |
(s |
, a) ( s , a), a, s . Другими слоами, каж- |
|||
|
k |
r |
j |
j |
|
|
дое состояние автомата M |
покрывается некоторым со- |
|||||
стоянием автомата |
M . В этом случае пишут M M |
|
||||
|
||||||
Пример. Имеются два автомата
Автомат М
Текущее
состояние
S |
0 |
|
|
S |
|
1 |
|
S2
Следующее
состояние
0 |
1 |
S |
0 |
S |
|
|
1 |
||
S |
|
S |
2 |
1 |
|
||
S0 |
S2 |
||
Выход
0 |
1 |
0 |
1 |
- |
1 |
1 |
1 |
|
|
Автомат
Текущее |
Следующее |
|
состояние |
состояние |
|
|
0 |
1 |
S |
0 |
' |
S |
0 |
' |
S |
1 |
' |
|
|
|
|
|
|
|||
S1 ' |
S0 |
' |
S1 |
' |
||||
Выход
01
01
11
M M |
|
, Автомат |
M |
покрывает M |
|
|
||
|
|
, т.к. состояния S0 |
||||||
покрывает S0 и S1 |
, а |
S1 ' покрывает |
|
|||||
S1 S2 . |
||||||||
|
|
Заметим, что вход 01010, считанный автоматом |
||||||
M |
в начальном состоянии S1 перерабатываются в -111- |
|||||||
, а |
M |
|
|
|
|
|
|
|
|
считанный в начальном состоянии S0 перераба- |
|||||||
тывается в 01111. При этом первый безразличный символ на выходе M отвечает 0 в M , а второй – соответствует 1 в M . Таким образом, в ходе работы безраз-

личная позиция в таблице для M может заполняться как нулем, так и единицей.
Опр.5. Выходная строка
b
совместима с выход-
ной строкой |
b ' , если в каждой позиции где символ обе- |
их строк определен и они совпадают. Пишут |
b b ' , ес- |
ли b совместим с |
b ' . |
Пример. Строка 01-1 совместима с 0111. 0-1-
совместима с 011-; но 010несовместимы с 011-. |
|
|
Отметим, что отношение совместимости |
|
не |
является отношением эквивалентности, так как оно рефлексивно, симметрично, но не транзитивно.
2.6.2. Понятия недетерминированного и вероятностного автомата
Недетерминированный автомат – это такой, который при данном входном символе и определенном состоянии может переходить в несколько различных внутренних состояний. Формально недетерминированный авто-
мат это пятерка |
(A, S, B, , ) такие что отображение |
: S A S - не |
является однозначным. Справедливо |
утверждение. Если недетерминированный автомат является конечным, то существует алгоритм, позволяющий построить конечный автомат, эквивалентный исходному автомату. При этом недетерминированный автомат имеет больше состояний, чем исходный недетерминированный автомат.
Вероятностный автомат представляет собой набор (A, S, B, , ) , где A, S, B - конечные множества , -
функция, определенная на множестве S A и принимающая в качестве своих значений вероятностные меры на множестве S . - функция, определенная на S A и принимающая в качестве своих значений вероятностные

меры на множестве B . Т.к. Sи B конечны, то соответствующие вероятностные меры задаются векторами
( p1 |
,.., pn ) и |
|
|
|
i |
i |
n |
|
m |
i |
1, |
i |
||
p , p 0, |
p |
p 1 |
||
|
|
i 1 |
|
i 1 |
( p |
',.., p |
m |
' )(| S | n,| B | m) |
1 |
|
|
|
|
Для задания функции |
|
использовано множе- |
||||||||||||||
ство стохастических матриц M1,..., Ms . |
n n , где |
|||||||||||||||||
Mi |
(i)is |
,i 1..s причем |
(i)is |
вероятность перехода |
||||||||||||||
автомата из S j |
в Sk |
под действием последовательности |
||||||||||||||||
ai . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, |
для задания |
|
использована систе- |
|||||||||||||
ма |
|
стохастических |
матриц |
|
|
размерности |
m n . |
|||||||||||
M |
,..., M |
s |
M |
|
|
(i) |
, |
где |
|
(i ) |
- вероятность появ- |
|||||||
i |
|
jk |
|
jk |
||||||||||||||
|
1 |
|
|
|
|
|
|
|||||||||||
ления на входе символа |
bk |
, если автомат находится в |
||||||||||||||||
состоянии в |
S |
j |
и на его вход поступает ai . |
|
|
|||||||||||||
|
|
|
||||||||||||||||
2.7. Процедура минимизации не полностью описанного автомата
2.7.1. Совместимые состояния
Определение. Состояние |
называется совместимым по |
|||||
выходу |
|
|
с |
состоянием |
, |
|
ли |
( |
) ля все |
. В этом случае пишет- |
|||
ся |
.Если состояния не совместимы по выходу, то |
|||||
пишут |
|
|
|
|
|
|
Например для автомата |
|
|
|
|||
Текущее |
|
Следующее |
|
Выход |
|
|
состояние |
|
состояние |
|
|
|
|
