
Пособие ДМ2
.pdf
( ) , ( ) , ( ) , ( )
Обозначим через x, y, z и w – число столбцов матрицы ̃ каждого из 4 видов соответственно. Тогда из условия ортогональности строк (3) получаем систему уравнений
x + t + z + w = n |
(1x1) |
x – y + z – w = 0 |
(1x2) |
x + y – z – w = 0 |
(1x3) |
x – y – z + w = 0 |
(2x3) |
Данная система уравнений имеет единственное решение x = y = z = w =
Таким образом при n имеем n = 4 , где - натуральное число.
Например, случай n=3 исключается, так как два вектора
размерности 3 с координатами |
не могут быть ортогональ- |
ными. |
|
Таким образом, матрицы Адамара могут существовать для всех порядков, кратных четырем. Для их построения используются разнообразные методы. Так, для n матрицы Адамара были построены для всех порядков, кратных 4 за ис-
ключением n = 116, 156, 188.
1.8.3. Построение матриц Адамара
Рассмотрим способ построения матриц Адамара исходя
из матриц Адамара меньшего порядка. |
|
Кронекеровым произведением |
матрицы A = (aij) |
i,j=1,2,..,m на матрицу B = (bij) i,j = 1,2,..,n называется (mn
) матрица вида = (aijB), i,j=1,2,..,m.
Имеют место следующие свойства кронекерова произведения матриц (исходя из определения):
1) |
, где - скаляр. |
2) |
. |
3) |
. |
4) |
. |
5) |
. |
Здесь A,A1,A2,C и B,B1,B2,D - матрицы порядков m и n соответственно.
Теорема. Кронекерово произведение матриц Адамара порядков m и n есть матрица Адамара порядка mn.
Доказательство. Пусть Hm и Hn - матрицы Адамара порядков m и n соответственно. Тогда для их кронекерова произведения имеем
=
. |
|
Отсюда в соответствии с (1) следует, что Hmn есть матри- |
|
ца Адамара порядка mn. |
|
Следствие. Для любого |
матрица Адамара |
существует |
|
Действительно при |
матрица |
(d раз), |
где H2 - матрица вида |
(4). Согласно теореме она есть матрица Адамара.
2.ТЕОРИЯ АВТОМАТОВ
2.1.Понятие конечного автомата
2.1.1.Общие сведения о конечных автоматах
Данный раздел посвящен математическому описанию работы цифровых вычислительных машин (ЦВМ) с помощью понятий множества, отношения, функции и графа. При этом из рассмотрения исключаются аналоговые вычислительные машины, состояние которых меняется непрерывно. Не рассматриваются также гибридные устройства, сочетающие цифровые и аналоговые компоненты. С математической точки зрения, все многообразие ЦВМ можно отнести к одному классу конечных автоматов.
Они обладают следующими свойствами:
1)Любая ЦВМ состоит из конечного числа элементов, каждый из которых в любой момент времени может находиться лишь в одном из конечного числа устойчивых состояний. Поэтому вся машина в целом имеет конечное множество состояний.
2)Любая ЦВМ работает последовательно, то есть
ееоперации синхронизированы сигналами тщательно настроенных электронных часов. В связи с этим состояние машины меняется в четкой последовательности.
3)ЦВМ является детерминированным устройством. Это значит, что при наличии полной информации о внутренних состояниях всех элементов машины и всех ее входов следующее состояние машины определяется однозначно.
ЦВМ делятся на универсальные и специализированные. В теории конечных автоматов анализируются универсальные машины, которые используются для любых целей.
С функциональной точки зрения современные ЦВМ состоят из 5 типов устройств:
1)устройство ввода;
2)устройство памяти;
3)арифметико-логическое устройство;
4)устройство управления;
5)устройство вывода.
ЦВМ конструируются на электронных схемах, имеющих два устойчивых состояния. Основная причина – технологическая. Но в этом случае возрастает также надежность электронных схем. Это связано с тем, что небольшие отклонения характеристик электронных схем не отражаются на работе всего устройства в целом.
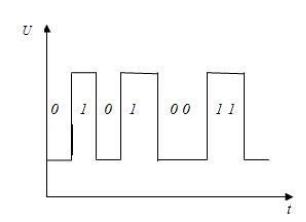
Таким образом, типичный сигнал в элементах ЦВМ имеет следующий вид
При этом единицей кодируется сигнал более высокого уровня, а нулём – более низкого. Или более точно, устанавливается некоторое пороговое значение сигнала и далее сигналы выше порога кодируются 1, а ниже – 0. Таким образом, не вникая в дальнейшие особенности работы электронных схем, отметим, что сигналы в таких устройствах двузначны. Это
значит, что переменные, используемые для их описания, принимают только два значения. Это же замечания относится и к материальным носителям информации и к преобразователям сигналов. В результате состояние любой ЦВМ, имеющей конечное число r двоичных элементов математически может быть описано следующим образом.
Нумеруются элементы ЭВМ, затем с каждым устойчивым состоянием связывается вектор
̅ |
. |
|
При этом координате |
приписывается значение 1, если |
|
i -й элемент находится в единичном состоянии, и 0, если |
i -й |
|
элемент находится в нулевом состоянии. |
|
|
2.1.2. Абстрактное определение конечного автомата
Абстрактным описанием ЦВМ служит математическое понятие конечного автомата.
Определение. Конечным автоматом называется набор из
пяти объектов: |
|
|
|
|
|
|
||
A, S, B, , |
|
, где |
|
|||||
|
|
|
|
|
|
|||
A a |
,...., a |
n |
|
- |
конечный список входных символов |
|||
1 |
|
|
|
|
||||
(входной алфавит); |
|
|
|
|
||||
B b |
,...,b |
|
|
|
|
- список выходных символов (выходной |
||
1 |
|
m |
|
|||||
алфавит); |
|
|
|
|
|
|
|
|
S s |
|
,...,s |
r |
|
|
- множество внутренних состояний; |
||
1 |
|
|
|
|||||
: S A S - |
функция перехода в следующее со- |
|||||||
стояние;
: S A B - функция выхода.
Таким образом, конечный автомат математически описывается тремя множествами и двумя функциями. Его действие состоит в том, что он считывает последовательность входных символов (программу), а затем печатает последова-
тельность выходных символов. Это действие происходит последовательно, а именно, конечный автомат, находящийся во
внутреннем |
состоянии |
считывает входной символ |
ak . |
Функция |
на паре |
принимает значение bi , которое |
|
печатается в качестве выходного символа. Функция |
на той |
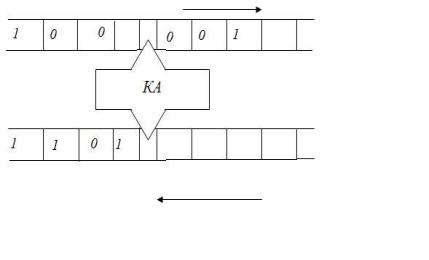
же паре принимает значение , которое является следующим внутренним значением автомата. Далее автомат считывает новый входной символ, печатает выходной, переходит в следующее состояние и так далее. Эту последовательность работы можно наглядно представить в следующем виде.
Входная
лента
Выходная
лента
В определении конечного автомата предполагается, что
функции |
|
и |
|
всюду определены. Такое описание автомата |
|
|
называется полным. |
|
|
|
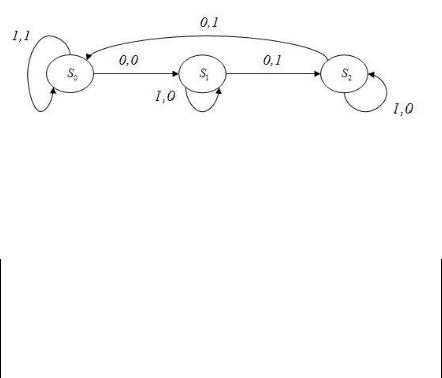
Пример. Автомат M A, S, B, , имеет входной ал- |
|||
фавит |
A 0,1 , выходной алфавит |
B 0,1 , |
множество |
внутренних состояний |
.Функции |
перехода и |
|
выхода задаются предписаниями: |
|
|
|

: |
: |
Подадим на вход последовательность 0,1,0,1. Если автомат находился в состоянии , то считав первый символ 0, он перейдёт в состояние и напечатает 0. Считав затем 1, он перейдёт в состояние и напечатает 0. Считав следующий 0, он перейдёт в состояние и напечатает 1. Наконец, считав последний символ 1, автомат закончит работу в состоянии , печатая 0. Таким образом, автомат преобразовал входной сигнал 0101 в сигнал 0010 на выходе.
Возможны следующие способы описания конечного автомата:
1) С помощью диаграммы состояний, которая представляет собой ориентированный граф. Вершины этого графа помечаются символами, обозначающими внутренние состояния автомата. А каждая дуга помечается упорядоченной парой
символов |
(a,b) . Первый символ |
a |
есть входной символ, вы- |
зывающий переход автомата в следующее состояние. Второй
символ |
b |
- выходной символ, который автомат печатает. Диа- |
|
грамма состояния для выше приведённого примера имеет вид.
2) Второй способ описания конечного автомата - таблица состояний – это табличное представление функций и . В соответствии с примером
Текущее |
|
Следующее состояние |
|
Выход |
|
||
состояние |
|
0 |
1 |
|
0 |
|
1 |
S0 |
|
S1 |
S0 |
|
0 |
1 |
|||
|
|
|
|
|
|
|
|||
S1 |
|
S2 |
S1 |
|
1 |
0 |
|||
|
|
|
|
|
|
|
|
|
|
S |
2 |
|
S |
2 |
S |
0 |
|
1 |
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Оба способа описания конечного автомата имеют свои преимущества и недостатки. Таблица состояний удобна при вычислениях, а диаграмма состояний является более наглядной. В частности, по диаграмме состояний конечного автомата можно обнаружить состояния недостижимые из других состояний. Например:

На этом рисунке показана диаграмма состояний конечного
автомата, у которого состояние |
недостижимо, если автомат |
начинает работу из состояний |
или . |
2.2.Эквивалентности в автоматах
2.2.1.Основные определения
Пусть на вход конечного автомата подается последовательность символов из входного алфавита A. Эту последовательность обозначают ̅, и называют строкой или вектором.
̅
На выходе конечного автомата печатается выходная строка
̅ |
|
, |
состоящая из символов алфавита |
B |
. |
|
||
Строка внутренних состояний . ̅ |
|
|
Для некоторого автомата |
|
по любой |
входной строки длины , и по любому начальному состоянию
однозначно определяется строка длины |
r |
внутренних |
|
|
|||
состояний. ̅ |
, которая получается примене- |
||
нием отображения , т.е. |
|
|
|
( |
) |
|
|
Аналогично, выходная строка ̅ определяется последовательным применением отображения , т.е.
( )
Поэтому рассматривая конечный автомат, как устройство,
перерабатывающее пары |
и ̅ |
в строки |
̅ |
и ̅ |
, |
Можно определить функции |
|
|
Эти функции рекурсивно строятся по известным φ и ψ, задающихся в описании автомата M.
Здесь Ar - множество всех строк длины r из алфавита A, а
Br и Sr - множества всех строк длины r из алфавитов B и S соответственно
