1.7.2. Трансверсали

Пусть дано множество мощностиnи множество,элементы которого являются подмножествами множестваS, т.е. .,. При этом допускается чтопри

Системой различных представителей (транверсалью)для совокупности множествM(S) называется множество элементов мощностиmиз множестваSи таких, что

1. ,

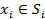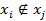2. , при.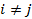

Критерием существования трансверсали для M(S) служит следующая теорема.

Теорема Холла.Совокупность множествM(S) имеет трансверсаль тогда и только тогда, когда для любогоk и любойk– выборки без повторенийиз множестваиндексов выполняется следующее неравенство

то есть число элементов объединения множеств не меньшеk.

Если для некоторого подсемейства семействаM(S) имеет место равенство

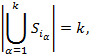
то такое подсемейство называется критическим.

1.7.3. Пермамент матрицы

Рассматривается матрица A= (a_ij),,,.

ПерманентомматрицыAназывается число, определяемое следующим выражением

Где суммирование производится по всевозможным выборкам объема nизmразличных элементов.

Рассмотрим примеры

Если m=n, то суммирование производится по всевозможным перестановкам элементов 1,2,…,n; а пермамент матрицыА perA получается из определителя этой матрицы при условии, что все слагаемые соответствующей суммы берутся с положительными знаками.

Свойства перманентов.

1. Если строка матрицы Aсостоит полностью из нулей, тоperA=0.

2. Перманент матрицы инвариантен относительно любой перестановки строк и столбцов.

3. При умножении какой-либо строки (или столбца) на скаляр , перманент матрицы умножается на.

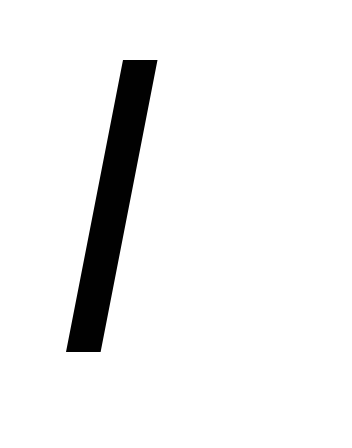4. Если Aквадратная матрица, тоper A^T = per A.

5. Если A_ij получена вычеркиванием изА i– строки иj–го столбца, - матрица, полученная изAзаменой элементаa_ij на 0, тогда

6. Разложение пермамента по i– строке.

Многие свойства перманента подобны свойствам определителя для квадратных матриц, однако свойство

вообще говоря не верно для перманентов. Перманент в отличие от определителя в общем случае не равен 0 при наличии строк (столбцов), линейно выражающихся через другие строки (столбцы).

1.7.4. Число трансверсалей

Важнейшее применение перманентов определяется следующей теоремой.

Теорема. ПустьA= (a_ij),i= 1,2,..,n,j= 1,2,..,m, , есть матрица инцидентности множеств, являющихся подмножествами множества.

То есть

Тогда для числа трансверсалей семейства имеет место равенство

Трансверсаль семейства существует тогда и только тогда, когда для соответствующей матрицы инцидентности выполняется условие.

Пример 1. (задача о встречах).Требуется определить число трансверсалей семейства, гдеX_i=X\{i} иx= {1,2,..,n}. Эта задача имеет и другие разнообразные формулировки, но обычно называетсязадачей о встречах. В данном случае матрицы инцидентности, где- символ Кронекера.

Обозначим h_n=per(1-δ_ij) и разлогая перманент по первой строке, получим

,

Где матрица получается из матрицызаменой элементаa₁₁ на 1.

Разлагая perA′_n-1 по элементуa₁₁получим

то есть получим рекуррентное соотношение

с начальными условиями h₀=1 иh₁=0

Перепишем рекуррентное соотношение в виде

h_n-nh_n-1=-(h_n-1-(n-1)h_n-2)=…=(-1)^k(h_n-k-(n-k)h_n-k-1)=…=(-1)ⁿ

Пологая , получим

Отсюда следует что

Таким образом, окончательный ответ

Пример 2.

Требуется найти число трансверсалей семейства (X_i , 1≤i≤n), где

X₁={1,2},X₂={1,2,3},X₃={2,3,4},…,X_n-1={n-2,n-1,n},X_n={n-1,n}, являющихся подмножествами множестваX={1,2,…,n}.

Решение.

Число трансверсалей

Разлагая этот перманент сначала по первой строке, а затем получившийся перманент разлагаем по первому столбцу, получаем рекуррентное соотношение

C_n=C_n-1+C_n-2

с начальным условием C₁=1,C₂=2

Полученные числа C_nявляются числами Фибоначчи.