
- •Министерство образования рф
- •2003 Г. Содержание
- •Введение.
- •Открытые и замкнутые множества.
- •1.2 Основные теоремы об открытых и замкнутых множествах.
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •1.4 Структура линейных замкнутых множеств из r.
- •Доказательство:
- •Мера ограниченного открытого множества: определение и свойства.
- •2.1 Определение меры ограниченного открытого множества.
- •2.2 Свойства мер открытых ограниченных множеств.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •5. Внутренняя мера множества и её свойства.
- •Мера Лебега: определение, свойства.
- •6.1 Определение меры Лебега.
- •6.2 Свойства меры Лебега.
- •Доказательство.
- •Измеримые множества и их свойства
- •7.1 Определение измеримых множеств.
- •7.2 Основные свойства измеримых множеств.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
1.4 Структура линейных замкнутых множеств из r.
Теорема
13: Для
того чтобы F![]()
ограниченное было замкнутым необходимо
и достаточно, чтобы оно являлось отрезком
или получена из этого отрезка удалением
из него конечного или счетного множества
попарно не пересекающихся интервалов,
концы которых не принадлежат F.
ограниченное было замкнутым необходимо
и достаточно, чтобы оно являлось отрезком
или получена из этого отрезка удалением
из него конечного или счетного множества
попарно не пересекающихся интервалов,
концы которых не принадлежат F.
Доказательство:
(необходимость)
Пусть
F
ограниченное замкнутое множество тогда
существует наименьший
![]() отрезок содержащийF.
отрезок содержащийF.
Возможны два случая:
1.
![]() =F;
=F;
![]() -отрезок,
-отрезок,![]() F
- отрезок
F
- отрезок![]() F
ограниченное замкнутое множество.
F
ограниченное замкнутое множество.
2.
![]()
![]() F,
т.е.
F,
т.е.
![]() \F
\F![]()
;
;![]() \F=
\F=![]() (дополнение
до
(дополнение
до![]() множестваF)
множестваF)
Возьмем
![]() не предельная точка дляF
не предельная точка дляF
![]()
![]()
![]() -
не внутренняя точка множества
-
не внутренняя точка множества![]() .
Т.к.
.
Т.к.![]() - произвольная точка, то
- произвольная точка, то![]() -
открыто. По теореме о строении ограниченных
открытых множеств
-
открыто. По теореме о строении ограниченных
открытых множеств![]() -
является объединением конечного или
счетного множества попарно не
пересекающихся интервалов, концы которых
не принадлежатG
(составляющих интервалов), удаляя из
них
-
является объединением конечного или
счетного множества попарно не
пересекающихся интервалов, концы которых
не принадлежатG
(составляющих интервалов), удаляя из
них
![]() получим замкнутое множество.
получим замкнутое множество.
(достаточность)
1.
Если
![]() =F;
=F;
![]() -отрезок,
-отрезок,![]() F
- отрезок
F
- отрезок![]() F
замкнутое множество.
F
замкнутое множество.
2.
Пусть F
получено из
![]() удалением из него конечного или счетного
множества попарно не пересекающихся
интервалов, концы которых не принадлежатF.
удалением из него конечного или счетного
множества попарно не пересекающихся
интервалов, концы которых не принадлежатF.
Пусть
G
– объединение удаляемых интервалов,
т.е.
![]() .
Как мы только что доказалиG-
открыто. Пусть
.
Как мы только что доказалиG-
открыто. Пусть
![]() ,x
не может быть предельной точкой для F
т.к. она принадлежит G
вместе с некоторой своей окрестностью.
Т.е. F
содержит все свои предельные точки,
т.е. F
–ограниченно.
,x
не может быть предельной точкой для F
т.к. она принадлежит G
вместе с некоторой своей окрестностью.
Т.е. F
содержит все свои предельные точки,
т.е. F
–ограниченно.
Следствие
4:
Для того чтобы F![]()
было замкнутым необходимо и достаточно,
чтобы оно являлось числовой прямой или
получено удалением из R
конечного или счетного множества
попарно не пересекающихся интервалов,
концы которых не принадлежат R.
было замкнутым необходимо и достаточно,
чтобы оно являлось числовой прямой или
получено удалением из R
конечного или счетного множества
попарно не пересекающихся интервалов,
концы которых не принадлежат R.
Мера ограниченного открытого множества: определение и свойства.
2.1 Определение меры ограниченного открытого множества.
Определение 1: Мерой интервала (a, b) a<b называется его длина, т.е. число m=m(0,1)=a-b m(a, b)>0.
Всякое открытое множество является объединением конечного или счетного множества попарно не пересекающихся интервалов, концы которых не принадлежат G (составляющих интервалов).
Пусть
G
– открытое множество.
![]() =
=
![]() .
Т.к.G
– открытое множество, то
.
Т.к.G
– открытое множество, то
![]() мера, которогоm=a-b.
Очевидно что
мера, которогоm=a-b.
Очевидно что
![]() .
Итак интервалы
.
Итак интервалы![]() попарно не пересекаются и содержатся
в интервале (a,b).
попарно не пересекаются и содержатся
в интервале (a,b).
Рассмотрим два случая:
G–конечное объединение интервалов
 .
т.е.G=
.
т.е.G=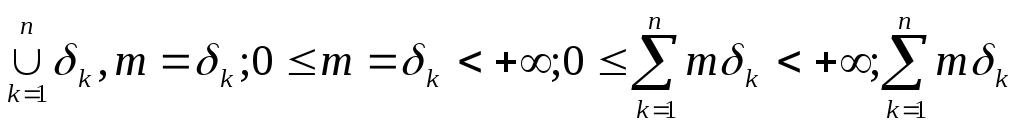 -
положительное число, выражающее
собственную сумму мер не пересекающихся
интервалов входящих в состав множестваG.
-
положительное число, выражающее
собственную сумму мер не пересекающихся
интервалов входящих в состав множестваG.
Пусть
 .
Рассмотрим ряд
.
Рассмотрим ряд -
положительный числовой ряд.
-
положительный числовой ряд.
(1)
![]() -
частичная сумма ряда
-
частичная сумма ряда
Последняя
частичная сумма
![]() возрастающая (т.к. члены ряда все
положительные) и ограничена сверху
(с.м. случай 1).
возрастающая (т.к. члены ряда все
положительные) и ограничена сверху
(с.м. случай 1).![]() по определению (1) сходиться и его сумма
есть не отрицательное число. ЕслиG
открытое ограниченное множество, то
сумма мер его составляющих интервалов
не отрицательное число, не большее чем
b-a.
по определению (1) сходиться и его сумма
есть не отрицательное число. ЕслиG
открытое ограниченное множество, то
сумма мер его составляющих интервалов
не отрицательное число, не большее чем
b-a.
Определение
2: Мерой
ограниченного открытого множества G
называется сумма мер его составляющих
интервалов. Ясно что
![]() .
.
2.2 Свойства мер открытых ограниченных множеств.
Теорема
1: Если
ограничено открытое множество G
является объединением конечного или
счетного числа попарно не пересекающихся
открытых множеств Gk,
то
![]() .
.
Доказательство:
![]() .
В правой части последнего равенства не
более чем счетное число интервалов.
Т.к.
.
В правой части последнего равенства не
более чем счетное число интервалов.
Т.к.
![]() не пересекаются попарно, то и интервалы
в последнем равенстве не пересекаются,
следовательно, они являются составляющими
интервалами для множестваG,
а, следовательно
не пересекаются попарно, то и интервалы
в последнем равенстве не пересекаются,
следовательно, они являются составляющими
интервалами для множестваG,
а, следовательно
![]() .
.
Теорема
2: Пусть
![]() -
ограниченно открытые множества, такие
что
-
ограниченно открытые множества, такие
что![]() .
Тогда
.
Тогда![]() .
.
Доказательство:
![]() .
Возьмем любой составной интервал
множества
.
Возьмем любой составной интервал
множества
![]() для него обязательно существует такой
составной интервал
для него обязательно существует такой
составной интервал![]() ,
что
,
что![]()
![]()
![]() ;
;![]() .
Проссумируем по к и в итоге получим:
.
Проссумируем по к и в итоге получим:![]()
![]()
![]()
![]() .
.
Мера ограниченного замкнутого множества: определение, свойства.
3.1 Определение меры ограниченного замкнутого множества.
Определение 1: Мерой пустого множества называется число 0.
Пусть
F
ограниченное замкнутое множество. тогда
существует наименьший отрезок
![]() содержит множествоF.
содержит множествоF.
![]() -
ограниченное открытое множество.
Следовательно, существует мера этого
множества. Т.к.
-
ограниченное открытое множество.
Следовательно, существует мера этого
множества. Т.к.![]()
Определение
2: Мерой
ограниченного замкнутого множества
F
называется число, обозначаемое mF,
и определяемое по формуле
![]() ,
где
,
где![]() - наименьшиё отрезок содержащий множествоF.
- наименьшиё отрезок содержащий множествоF.
3.2 Свойства мер ограниченных замкнутых множеств.
Теорема
1:
![]()
Доказательство:
![]()
Теорема 2: Пусть (a,b) и (c,d) не пересекающиеся отрезки, тогда мера их объединения равна сумме мер отрезков.
Доказательство:
![]()
Теорема
2: Пусть
F
ограниченное замкнутое множество
содержащиеся в интервале (c,d),
тогда
![]()
CF Д
 оказательство:
оказательство:










 Пусть
Пусть
![]() наименьший
наименьший
c а b d отрезок содержащий множество
F.
F
Тогда
по определению
![]()
![]()
Теорема
3: Пусть
![]() -
ограниченно замкнутые множества, такие
что
-
ограниченно замкнутые множества, такие
что![]() .
Тогда
.
Тогда![]() .
.
Доказательство:
Пусть
G
– открытое множество т.ч.
![]() (это
возможно сделать т.к.
(это
возможно сделать т.к.![]() ограниченно). Рассмотрим множество
ограниченно). Рассмотрим множество![]() -
открытое множество. Действительно
-
открытое множество. Действительно![]()
![]()
![]()
![]() .
.
![]() (умножим на -1 и прибавимmG)
(умножим на -1 и прибавимmG)
![]()
![]()
![]()
Внешняя мера множества и её свойства.
Пусть
E
– ограниченное множество.
![]() .
Возьмём всевозможные открытые множестваG
покрывающие множество E.
.
Возьмём всевозможные открытые множестваG
покрывающие множество E.
![]() .
.
Определение
1:
Пусть A
множество всевозможных множеств
покрывающих множество E.
Внешней мерой множества E
называется число, обозначаемое
![]() A(E)
– множество всевозможных множеств
содержащих множество E.
A(E)
– множество всевозможных множеств
содержащих множество E.
Выясним основные свойства внешней меры:
Свойство
1:
![]() .
.
Доказательство:
![]() .
.
Свойство
2: Если
![]() ,
то
,
то![]() .
.
Доказательство:
![]() -
множество всевозможных множеств
содержащих множество
-
множество всевозможных множеств
содержащих множество
![]() .
.
![]() -
множество всевозможных множеств
содержащих множество
-
множество всевозможных множеств
содержащих множество
![]() .
.
![]() .
Если область расширенно, то его область
значения может только уменьшиться, т.к.
.
Если область расширенно, то его область
значения может только уменьшиться, т.к.
![]() .
.
Свойство 3: Если множество Е представляет собой сумму конечного
или
счетного числа множеств
![]() (символически
(символически![]() ),
то
),
то
![]() (1)
(1)
Доказательство.
Фиксируем
произвольное
![]() >0.
По определению
меры
>0.
По определению
меры
![]() как точной нижней грани, для каждого
номераk
найдется
покрытие
как точной нижней грани, для каждого
номераk
найдется
покрытие
![]() множества
множества![]() системой интервалов
системой интервалов![]() (n=1,
2, ...) такое, что:
(n=1,
2, ...) такое, что:
![]() (2)
(2)
Обозначим
через S
покрытие всего Е,
объединяющее
все покрытия
![]() (k=1,
2,
...) и состоящее из всех интервалов
(k=1,
2,
...) и состоящее из всех интервалов
![]() (k
= 1, 2,...;
n=1,
2, ...)• Так как S
является покрытием Е,
то
m*E
(k
= 1, 2,...;
n=1,
2, ...)• Так как S
является покрытием Е,
то
m*E![]() ,
но
,
но
![]() .
.
Из последних двух соотношений и из (2) получим:
![]()
![]()
![]()
Будем
обозначать расстояние между множествами
![]()
![]() .
.
Свойство
4:Если![]() >0
то
>0
то
![]()
