
- •Министерство образования рф
- •2003 Г. Содержание
- •Введение.
- •Открытые и замкнутые множества.
- •1.2 Основные теоремы об открытых и замкнутых множествах.
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •1.4 Структура линейных замкнутых множеств из r.
- •Доказательство:
- •Мера ограниченного открытого множества: определение и свойства.
- •2.1 Определение меры ограниченного открытого множества.
- •2.2 Свойства мер открытых ограниченных множеств.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •5. Внутренняя мера множества и её свойства.
- •Мера Лебега: определение, свойства.
- •6.1 Определение меры Лебега.
- •6.2 Свойства меры Лебега.
- •Доказательство.
- •Измеримые множества и их свойства
- •7.1 Определение измеримых множеств.
- •7.2 Основные свойства измеримых множеств.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
- •Доказательство.
Открытые и замкнутые множества.
Определение открытых и замкнутых множеств.
При
![]() множество
множество![]() называется шаром с центром
называется шаром с центром![]() радиуса
радиуса![]() или также
или также![]() -окрестностью
точки
-окрестностью
точки![]() .
.
Определение 1: Множество Е называется открытым, если все его точки являются внутренними, т.е. если оно не содержит своих граничных точек. Исходя из, этого пустое множество следует считать открытым.
Пример 1: Любое n-мерный интеграл – открытое множество.
Определение
2: Множество
Е называется замкнутым, если оно содержит
все свои предельные точки, т.е. если
![]() .
Иначе если множество замкнуто, то оно
содержит свою границу, т.е.
.
Иначе если множество замкнуто, то оно
содержит свою границу, т.е.![]()
![]() .
Исходя из, этого пустое множество следует
считать замкнутым, хотя оно в то же время
является и открытым.
.
Исходя из, этого пустое множество следует
считать замкнутым, хотя оно в то же время
является и открытым.
Пример 2: Любой отрезок – замкнутое множество.
Следует обратить особое внимание на то что, классы замкнутых и открытых множеств не охватывают вместе всех множеств, кроме того, эти классы пересекаются. Существуют множества, которые не являются ни замкнутыми, ни открытыми, а так же множества, которые одновременно являются и замкнутыми, и открытыми.
Пример
3: Множество
R
рациональных точек
![]() ни замкнуто, ни открыто.
ни замкнуто, ни открыто.
Линейный полусегмент - ни замкнутое, ни открытое множество.
Докажем теперь теоремы характеризующие свойства открытых и замкнутых множеств.
1.2 Основные теоремы об открытых и замкнутых множествах.
Теорема
1:
Производное множество
![]() любого
множества E
замкнуто.
любого
множества E
замкнуто.
Доказательство:
Пусть
![]()
![]() в
любой окрестности
в
любой окрестности![]() точки
точки![]() имеются точки множества
имеются точки множества![]() отличные от
отличные от![]() .
Пусть
.
Пусть![]() .
Т.к.
.
Т.к.![]() предельная точка множестваE,
предельная точка множестваE,
![]() должна быть предельной для E
должна быть предельной для E
![]() .
Т.о.
.
Т.о.![]() содержит все свои предельные точки, а
это значит что оно является замкнутым.
содержит все свои предельные точки, а
это значит что оно является замкнутым.
Следует
заметить, что в частном случае производное
множество
![]() может оставаться пустым.
может оставаться пустым.
Теорема 2: Если множество F замкнуто, то его дополнение CF открыто.
Доказательство:
Пусть
![]() и
(в силу замкнутости F)
и
(в силу замкнутости F)
![]() .
Но это означает, что некоторая окрестностьV(x)
точки x
не принадлежит F
и поэтому принадлежит CF.
.
Но это означает, что некоторая окрестностьV(x)
точки x
не принадлежит F
и поэтому принадлежит CF.
Теорема 3: Если множество G открыто, то его дополнение CG замкнуто.
Доказательство:
любая
предельная точка x
множества CG
принадлежит этому множеству, т.к. в
противном случае
![]() .
А т.к. множествоG
открыто, то и некоторая окрестность
V(x)
точки x
не принадлежала бы G
и не принадлежала бы CG,
т.е. x
не являлась бы предельной точкой
множества CG.
.
А т.к. множествоG
открыто, то и некоторая окрестность
V(x)
точки x
не принадлежала бы G
и не принадлежала бы CG,
т.е. x
не являлась бы предельной точкой
множества CG.
Теорема 4: Сумма любого числа открытых множеств является открытым множеством.
Доказательство:
Пусть
Е - сумма любого числа открытых множеств
![]() и
и![]() .
Тогда (по определению суммы множеств)
.
Тогда (по определению суммы множеств)![]() (хотя
бы одному) и т.к.
(хотя
бы одному) и т.к.![]() - открытое, то и некоторая окрестностьV(x)
точки x
принадлежит хотя бы одному
- открытое, то и некоторая окрестностьV(x)
точки x
принадлежит хотя бы одному
![]() а
а![]() и множествуE.
и множествуE.
Теорема 5: Пересечение любого конечного числа открытых множеств является открытым множеством.
Доказательство:
Пусть
Е - пересечение любого конечного числа
открытых множеств
![]()
![]() .
Тогда
.
Тогда![]()
![]() ,
и поэтому найдется некоторая окрестность
,
и поэтому найдется некоторая окрестность![]() .
точкиx
принадлежащая
.
точкиx
принадлежащая
![]() .
Если
.
Если![]()
Теорема 6: Пересечение любого числа замкнутых множеств является замкнутым множеством.
Доказательство:
Пусть
Е - пересечение любого числа замкнутых
множеств
![]() .CE
представляет собой сумму всех дополнений
.CE
представляет собой сумму всех дополнений
![]() ,
каждое из которых является (по теореме
2) открытым множеством. По теореме 4CE
– открытое множество, а
,
каждое из которых является (по теореме
2) открытым множеством. По теореме 4CE
– открытое множество, а![]() по теореме 3E
– замкнутое множество.
по теореме 3E
– замкнутое множество.
Теорема 7: Сумма конечного числа замкнутых множеств является замкнутым множеством.
Доказательство:
Пусть
Е - сумма конечного числа замкнутых
множеств
![]() тогда
тогда![]() каждое, из которых является (по теореме
2) открытым множеством. По теореме 4CE
– открытое множество, а
каждое, из которых является (по теореме
2) открытым множеством. По теореме 4CE
– открытое множество, а![]() по теореме 3E
– замкнутое множество.
по теореме 3E
– замкнутое множество.
Теорема 8: Любой шар S(a,r) - открытое множество.
Доказательство:
Пусть
![]() .
Рассмотрим
.
Рассмотрим![]() .
.
Пусть
![]() ,
покажем что
,
покажем что![]() .
.![]() Следовательно, любой шарS(a,r)
- открытое множество.
Следовательно, любой шарS(a,r)
- открытое множество.
1.3 Структура открытых линейных множеств из R.
Определение
1:
Множество E
из R
называется ограниченным с верху (снизу)
если существует такая точка Q(P)
что для любых точек
![]()
![]() .
.
Определение
2:
Множество E
называется ограниченным, если оно
ограничено сверху и снизу, т.е. если
существует P,Q
такие что для любого
![]()
![]() .
.
Определение
3: Множество
E
называется ограниченным, если существует
положительное число M,
такое что для любого
![]()
![]() .
.
Определение
4:
Точка
![]() называется верхней гранью множестваE,
если правее точки M
нет точек множества E,
и для любого
называется верхней гранью множестваE,
если правее точки M
нет точек множества E,
и для любого
![]() >0
существует
>0
существует![]() лежащая правее точкиM-
лежащая правее точкиM-![]() .ОбозначаетсяM=sup
E=
.ОбозначаетсяM=sup
E=
 .
.
Определение
5: Точка
![]() называется нижней гранью множестваE
и обозначается m=infE=
называется нижней гранью множестваE
и обозначается m=infE=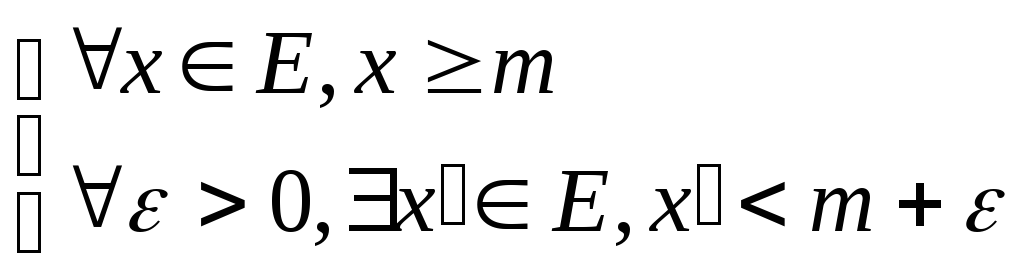 .
.
Теорема 9: Всякое не пустое ограниченное с верху (снизу) множество имеет верхнюю (нижнюю) грань.
Теорема 10: Если верхняя (нижняя) грань множества E существует, но не принадлежит E, то она является предельной точкой множества E.
