Глава 10. Построение кривой переходного процесса

10.1 Общие соображения

Построение переходных процессов в САУ, вызванных основными для данной системы воздействиями, является завершающим этапом исследования системы.

При нахождении переходного процесса в системе автоматического регулирования возникают две трудности.

Первая трудность - принципиального характера - заключается в том, что в реальных САР управляющие и возмущающие воздействия не являются известными функциями времени, а носят случайный характер. В связи с этим приходится рассматривать некоторые типичные воздействия. Причем, их выбирают такими, чтобы они были по возможности близкими к реальным воздействиям в САР.

Для следящих систем при g(t)=0 и систем стабилизации переходный процесс может строиться для случая приложения возмущающего воздействия, В качестве типовых используются возмущающие воздействия в виде единичной ступенчатой функции и в виде единичной импульсной функции. Эти возмущения рассмотрены нами на предыдущих лекциях,

Вторая трудность - непринципиального характера - заключается в том, что обычно САР описывается дифференциальными уравнениями сравнительно высокого порядка. Это усложняет практические расчеты; поэтому для облегчения задачи построения кривой переходного процесса во многих случаях приходится пользоваться приближенными методами, а также применять вычислительный устройства как непрерывного, так и дискретного действия.

Существует три группы методов построения переходных процессов: аналитические методы, графические методы и построение переходных процессов с помощью вычислительных машин (машинные методы).

10.2 Аналитические методы

Основаны на решении дифференциального уравнения системы

D(p)x(t) = M(p)f(t) (10.1)

Решением линейного дифференциального уравнения с постоянными коэффициентами будет выражение вида:

x(t) = x_п(t) + x_в(t) (10.2)

где x_п(t) - общее решение однородного дифференциального уравнения D(p)x(t) = 0, имеющее вид:

(10.3)

причем c₁, ..., c_n - произвольные постоянные, определяемые из начальных условий процесса, а p₁, ..., p_n - корни характеристического уравнения D(p) = 0.

Частное или вынужденное решение x_в(t) определяется правой частью уравнения (10.1) и оно соответствует некоторому установившемуся режиму в системе, который будет существовать после затухания x_п(t).

Таким образом, в общем случае мы имеем дело с задачей решения неоднородного дифференциального уравнения.

Для типового входного воздействия в виде единичной ступенчатой функции решение неоднородного уравнения (10.1) может быть сведено к решению уравнения без правой части переходом к другой переменной.

Примем, что f(t)=1(t), причем единица имеет размерность переменной, стоящей в правой части (10.1), а и. С учетом этого, (10.1) примет вид:

(10.4)

Тогда установившееся значение переменной х при t:

(10.5)

Это установившееся значение представляет собой частное или вынужденное решение неоднородного дифференциального уравнения (10.1), т.е. x_в(t) = x_уст.

Введем новую переменную:

z(t) = x(t) - x_в(t) = x(t) - x_уст. (10.6)

Решение неоднородного уравнения (10.1) для z(t) может быть записано в виде:

(10.7)

т.е. этому решению соответствует исходное дифференциальное уравнение без правой части (D(p)x(t) = 0).

Для отыскания решения этого уравнения также необходимо определить корни (полюсы) характеристического уравнения:

(10.8)

и постоянные интегрирования c₁, c₂, ..., c_n. Для определения постоянных интегрирования c₁, c₂, ..., c_n используется начальное условие: при t = 0, х(0) = х₀, х^’(0) = х₀^’ ... , х^(n-1)(0) = х₀^(n-1) . Начальные условия находятся на основании физических соображений из дифференциального уравнения (10.1). Дифференцируя (10.2) по времени n-1 раз и используя начальные условия, получают n алгебраических уравнений, куда входят n неизвестных постоянных времени. Таким образом, приходится иметь дело с двумя трудоемкими операциями: вычислением корней и отысканием постоянных интегрирования. Если первая операция может быть выполнена приближенными методами, то вторая является весьма трудоемкой. Задача несколько облегчается, если для решения использовать операторный метод и преобразование Лапласа. Напомним, что применяя прямое преобразование, мы заменяем операции дифференцирования и интегрирования оригинала алгебраическими действиями по отношению к изображениям. Затем путем применения обратного преобразования Лапласа получаем функцию х(t).

Следует отметить, что преобразование Лапласа применимо к функции х(t), если она удовлетворяет следующим условиям:

1. x(t) = 0, если t < 0

2. можно выбрать такое положительное число с, при котором.

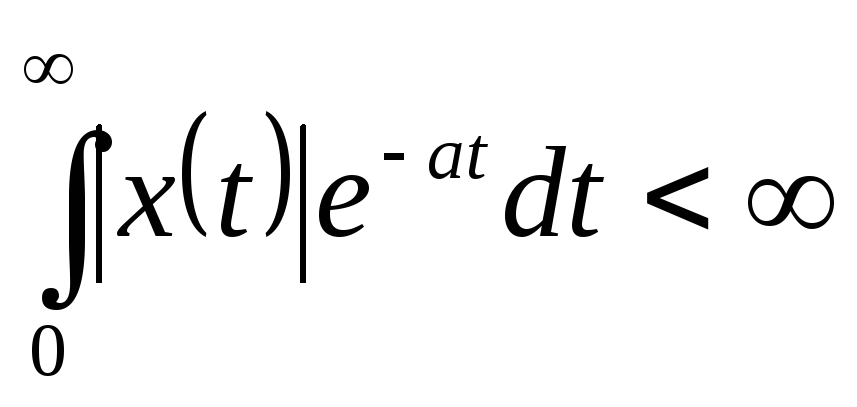Для отыскания оригинала х(t) по его изображению X(р) можно пользоваться таблицами изображений и существующими теоремами, в частности теоремой разложения, которая устанавливает следующее: если изображение Лапласа имеет вид отношения двух многочленов:

(10.9)

то при отсутствии нулевых корней знаменателя:

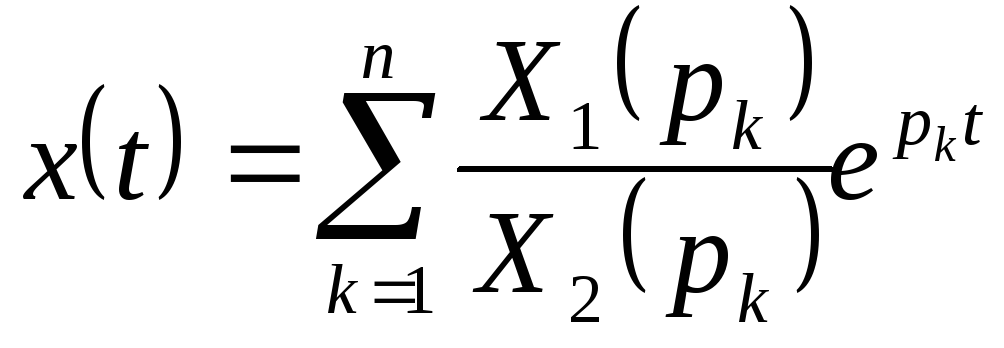(10.10)

где р_1,2 - некратные корни знаменателя (10.9).

Если знаменатель изображения Лапласа имеет нулевой корень (р₀ = 0), то изображение надо представить в виде:

(10.11)

Тогда оригинал может быть найден по формуле:

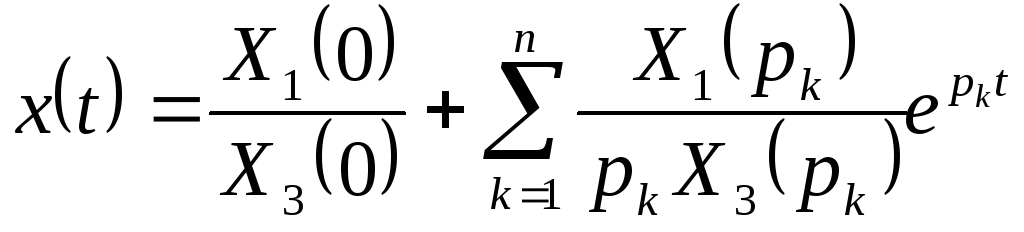(10.13)

Как видно из выражений (10.9-10.13), операторный метод также имеет ограниченные возможности и применим, если достаточно просто находятся корни характеристического уравнения. В противном случае применяют графические методы.