5. Типовые воздействия и временные характеристики систем (элементов) автоматического управления

В реальных условиях в большинстве случаев САУ подвержена действию управляющих и возмущающих воздействий произвольной формы и носящих случайный характер. Поэтому при исследованиях САУ приходится ориентироваться на типовые законы изменения внешних воздействий, в качестве которых принимают либо наиболее вероятные, либо наиболее неблагоприятные законы изменения управляющего и возмущающего воздействия.

В качестве типовых воздействий в ТАУ используются единичная ступенчатая функция (единичный скачок), единичная импульсная функция и гармоническое воздействие.

1. Единичная ступенчатая функция 1(t).

Эта функция (рисунок 2.7,а) определяется следующим образом:

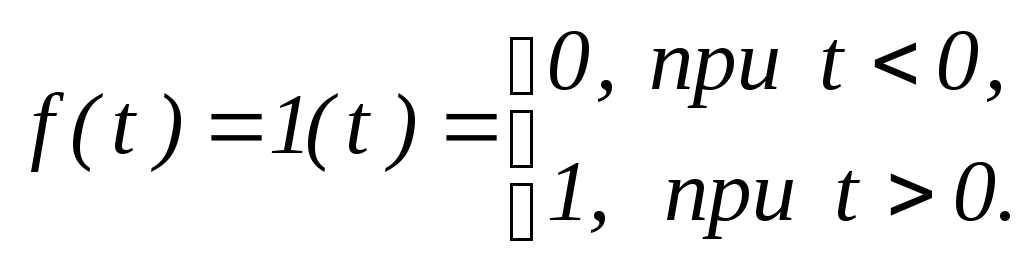, (2.53)

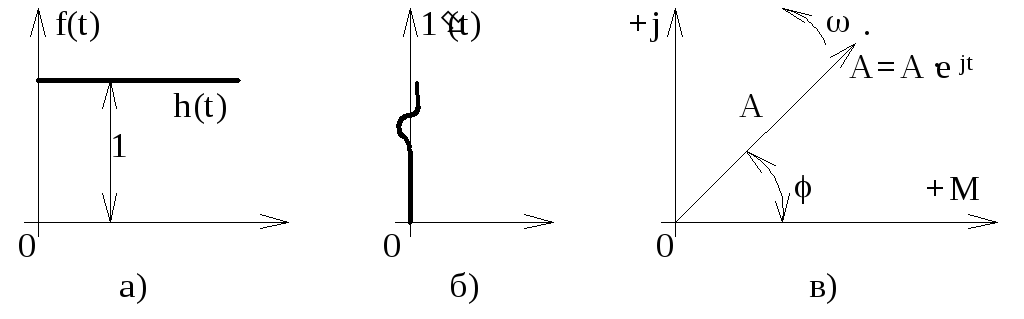
Рисунок 2.7 Типовые воздействия САУ

Изображение Лапласа такой функции будет иметь вид:

, (2.54)

Такое воздействие имеет место в системах стабилизации при перенастройке САР на другое воздействие, скачкообразном изменении нагрузки на валу двигателя, напряжения на его якоре и т.д.

2. Единичная импульсная функция δ(t).

Эту функцию можно рассматривать как производную от единичной ступенчатой функции.

Хотя функция 1(t)в обычном смысле не является дифференцируемой, но на нее путем предельного перехода можно распространить понятие производной, так как

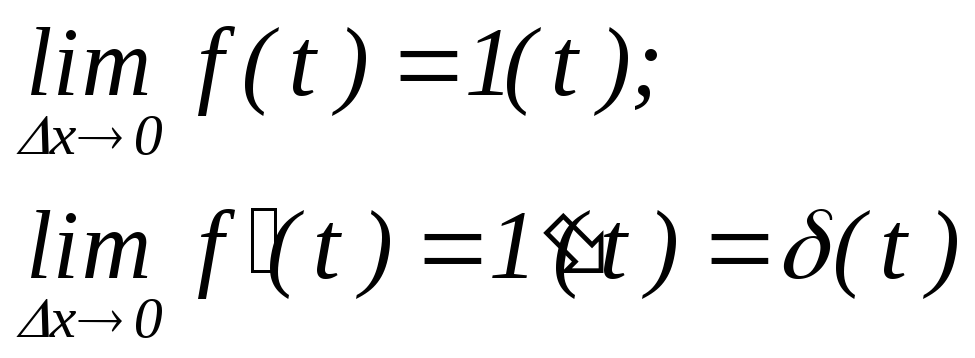_(2.55)

Единичную импульсную функцию можно рассматривать как предел одностороннего прямоугольного импульса высотой и длительностиΔt приΔt→0. Площадь импульса . Поэтому при переходе к пределу приΔt→0получается мгновенный импульс (нулевой продолжительности с бесконечным значениемh), но величина импульса (площадь) при этом равна единице.

Реально в природе отсутствуют мгновенные импульсные изменения физических величин во времени. Однако в случае, если продолжительность мала по сравнению со временем протекания переходного процесса, вызванного ими, то с большой степенью точности реальное импульсное воздействие может быть заменено единичным с некоторым коэффициентом, определяемым площадью реального импульса.

Единичной импульсной функции (рисунок 2.7, б) соответствует изображение

_(2.56)

3. Гармоническое воздействие.

Это воздействие может быть задано как вещественная функция времени или в комплексной форме.

В вещественной форме гармоническое воздействие может быть представлено в виде синусоидальной или косинусоидальной функции времени:

f(t)=Asin(t+); f(t)=Acos(t+), (2.57)

где - круговая частота;

 - начальная фаза;

А- амплитуда.

При A=1получим единичное гармоническое воздействие.

В комплексной форме гармоническая функция задается на комплексной плоскости в виде вектора (рисунок 2.7,в).

Этот вектор можно выразить в показательной форме

Если вектор , начиная с момента времениt=0, вращается против часовой стрелки, то ему соответствует следующая комплексная функция времени

, (2.58)

Гармоническое воздействие широко применяется для исследования САУ в качестве входного воздействия.

4. Временные характеристики сау.

Временными характеристиками системы называются зависимости выходной величины от времени при входной величине, изменяющейся по заданному закону. В качестве таких характеристик рассматривается переходная и весовая функции.

Реакция системы (элемента) автоматического управления на единичную ступенчатую функцию при условии, что система (элемент) до приложения воздействия находилась в покое, называется переходной функцией h(t).

Переходную функцию можно получить как решение неоднородного дифференциального уравнения системы, правой частью которого является единичная ступенчатая функция. Выражение для переходной функции будет иметь вид

, (2.59)

Реакция САУ на единичную импульсную функцию при условии, что система до приложения воздействия находилась в покое, называется весовой функцией w(t).

, (2.60) тогда

, (2.61)

то есть передаточную функцию системы автоматического управления можно определить как изображение по Лапласу весовой функции.

Из определения весовой функции следует

, (2.62) то есть

(2.63)

5. Частотные характеристики САУ

Пусть линейная САУ описывается дифференциальным уравнением

, (2.64) где D(p)=a₀ pⁿ+a₁ p^n-1+...+a_n , K(p)=b₀ p^m+b₁ p^m-1+...+b_m .

Рассмотрим установившийся режим в системе, когда входным воздействием является гармоническая функция времени

, (2.65)

В устойчивой системе, в которой затухает свободная составляющая переходного процесса по истечении достаточно большого промежутка времени, устанавливается периодический процесс той же частоты ϖ, но с другой амплитудойВи фазой, величина которых зависит отϖ.

, (2.66)

Дифференцируя периодическую функцию получим

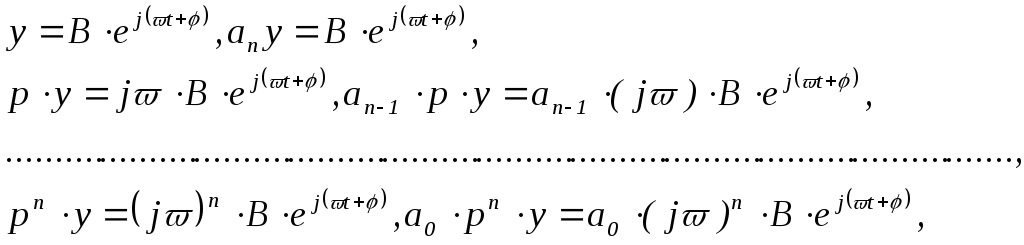
Суммируя полученные равенства почленно, получим

, (2.67)

Таким образом, символическое выражение D(p)yпри гармоническомyпереходит в алгебраическое комплексное выражение.

Аналогично

, (2.68)

Подставляя (2.67) и (2.68) в (2.64) и сокращая на e^{jϖ t}, найдем

, (2.69)

откуда

, (2.70) или

, (2.71)

Выражение (2.70) характеризует частотные характеристики системы и называется частотной передаточной функцией или комплексным коэффициентом усиления системы.

Таким образом, комплексным коэффициентом усиления системы (звена) называется отношение комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе при подаче на вход синусоидального воздействия

, (2.72)

Это комплексное число, модуль которого равен отношению амплитуд выходной и входной величин, а аргумент - сдвигу фаз выходной величины по отношению к входной.

, (2.73)

.

Из сравнения выражений для передаточных функций (2.252.28) и комплексного коэффициента усиления легко убедиться, что частотная передаточная функция (комплексный коэффициент усиления) легко получается из обычной путем простой заменыp=jϖ.

По аналогии с комплексными числами комплексный коэффициент усиления можно представить в показательной форме или как сумму действительной и мнимой составляющих, то есть

, (2.74)

Если изменять частоту входного воздействия ϖот 0 до, то комплексный коэффициент усиления будет изменяться

, (2.75)

При этом конец вектора W(jϖ)будет скользить по кривой, которая называется частотным годографом комплексного коэффициента усиления или комплексной частотной характеристикой звена, или амплитудно-фазовой частотной характеристикой (АФХ). АФХ строится на комплексной плоскости. По оси абсцисс откладывается вещественнаяU(ϖ), а по оси ординат мнимаяV(ϖ)составляющие комплексного коэффициента усиления. АФХ представляет собой геометрическое место концов векторов (годограф), соответствующихW(jϖ)при изменении частоты от нуля до бесконечности. Для каждой частоты на плоскости соответствует точка. Полученные точки соединяются плавной кривой (рисунок 2.8). АФХ может быть построена как для положительных, так и для отрицательных частот. При замене в частотной передаточной функции+ϖна-ϖполучится сопряженная комплексная система. Поэтому, АФХ для отрицательных частот может быть построена, как зеркальное изображение относительно вещественной оси АФХ для положительных частот. В большинстве случаев при исследовании САУ ограничиваются построением АФХ для положительных частот.

Вместо АФХ можно построить отдельно амплитудно-частотную характеристику (АЧХ) и фазочастотную характеристику (ФЧХ). Для этого частотную передаточную функцию представляют в показательной форме

, (2.76)

где - модуль вектора, равный его длине. Это и есть амплитудно-частотная характеристика (АЧХ) (рисунок 2.9).

- аргумент (фаза) вектора - угол его поворота. Это фазочастотная характеристика (ФЧХ) (рисунок 2.10).

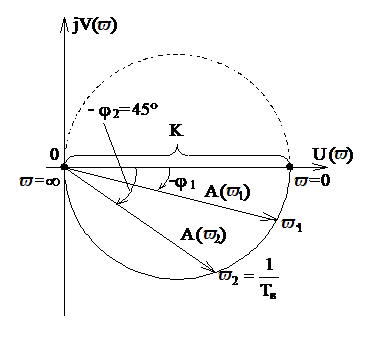
Рисунок 2.8 Амплитудно-фазовая частотная характеристика

Амплитудно-частотная характеристика показывает, как пропускает звено сигналы различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.

Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном (системой) на различных частотах.

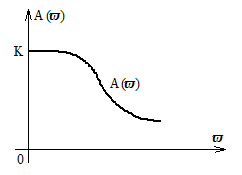
Рисунок 2.9 Амплитудно-частотная характеристика

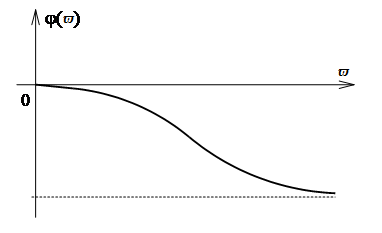
Рисунок 2.10 Фазочастотная характеристика

При исследованиях САУ часто пользуются вещественной и мнимой частотными характеристиками, которые строятся по функциям U(ϖ)(рисунок 2.11) иV(ϖ) (рисунок 2.12).

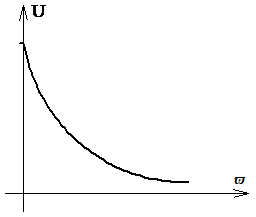
Рисунок 2.11 Вещественная частотная характеристика

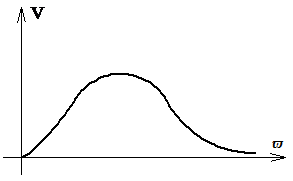
Рисунок 2.12 Мнимая частотная характеристика

Для каждого фиксированного ϖзначениеW(jϖ)однозначно определяет точку на комплексной плоскости с декартовыми координатамиU(ϖ)иV(ϖ)или полярными координатамиА(ϖ)и(ϖ).Поэтому, легко видеть, что амплитудная, фазовая, вещественная и мнимая частотные характеристики выражаются друг через друга посредством следующих соотношений (рисунок 2.8)

, (2.77)

, (2.78) и, наоборот,

, (2.79)

, (2.80)

Эти соотношения по сути дела и есть формулы перехода от полярных координат к прямоугольным и, наоборот, от прямоугольных координат к полярным.

Такие системы, в которых функция U(ϖ)однозначно определяет(ϖ)и, наоборот, функцияА(ϖ)однозначно определяет(ϖ), называются минимально-фазовыми системами.

Исходя из данных выводов и определений, можно предложить простую экспериментальную методику построения АФХ, АЧХ, ФЧХ при синусоидальном входном воздействии. Эта методика хорошо иллюстрирует физический смысл частотных характеристик САУ.

1. На вход исследуемой САУ (звена) подают синусоидальный сигнал с различной частотой ϖ.

2. Для фиксированной частоты ϖ₁осциллографируютx(t)иy(t)(рисунок 2.13).

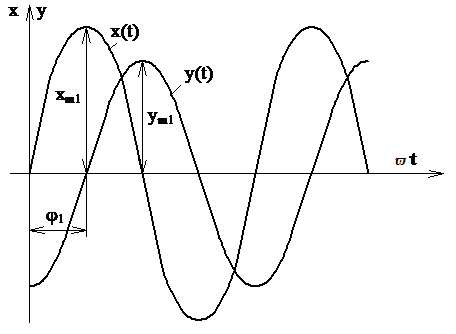
Рисунок 2.13 Гармонический сигнал на входе x(t) и на выходе y(t) САУ

3. Измеряют x_m1, y_m1и₁при₁

4. Находят 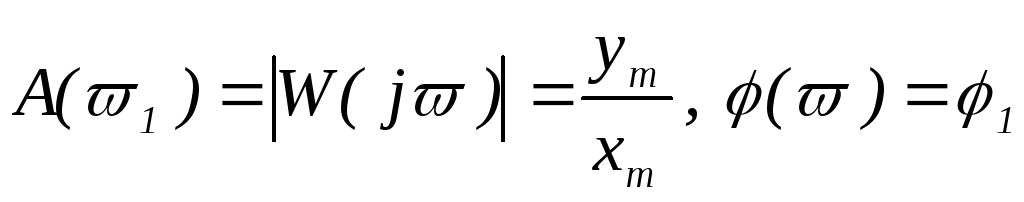и строят одну точку АФХ, АЧХ и ФЧХ (рисунок 2.14).

Рисунок 2.14 Экспериментальное построение частотных характеристик:

а - АЧХ, б - ФЧХ, в - АФХ

5) Задают гармонический сигнал с новой частотой ₂и строят следующую точку характеристики и т.д.

В качестве примера построим частотные характеристики генератора (рисунок 2.14,б).

Для перехода от операторной формы записи (2.35) к частотной передаточной функции достаточно заменить p=jϖ.

, (2.81)

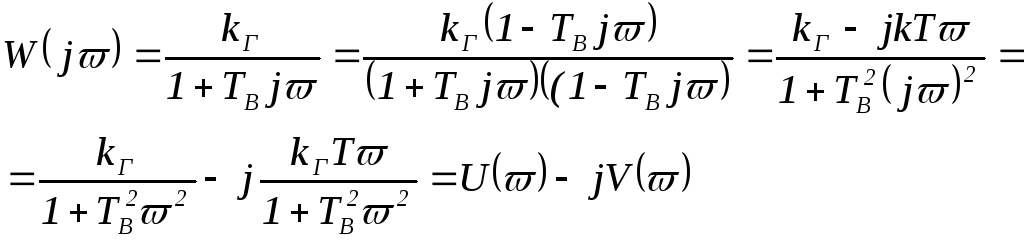, (2.82)

Изменяя > ϖ>0, получим

при ϖ =0: U(ϖ)=K, V(ϖ)=0,

при =: U(ϖ)=0, V(ϖ)=0.

Построение АФХ произведено на рисунке 2.8.

Найдя модуль АФХ, получим амплитудную частотную характеристику.

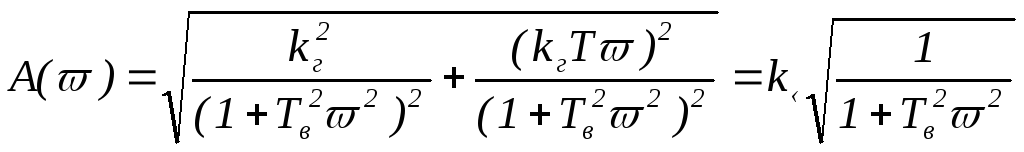, (2.81а)

АЧХ, соответствующая этому выражению, построена на рисунке 2.9.

Построим фазовую частотную характеристику.

,

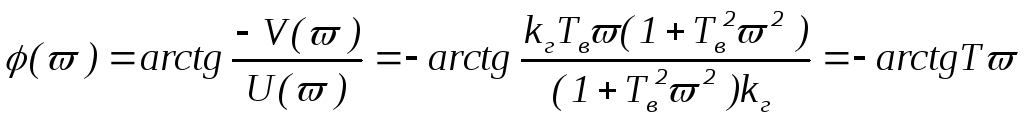(2.83)

График для этой ФЧХ построен на рисунке 2.10.

Определение модуля АФХ (АЧХ) по выражению (2.79) при больших порядках дифференциального уравнения, описывающего поведение координат системы, сопряжено с большими вычислительными трудностями, так как приходится умножать знаменатель и числитель передаточной функции на сопряженное комплексное число, что повышает порядок выражения вдвое.

Трудности, связанные с вычислением амплитудно-частотной характеристики, можно значительно уменьшить, если воспользоваться правилами умножения и деления комплексных чисел. Известно, что при умножении комплексных чисел модули их перемножаются, а аргументы складываются, то есть если z1, z2, ..., znкомплексные числа, то

, (2.84)

, (2.85)

При делении комплексных чисел модуль делимого делится на модуль делителя и из аргумента делимого вычитается аргумент делителя, то есть

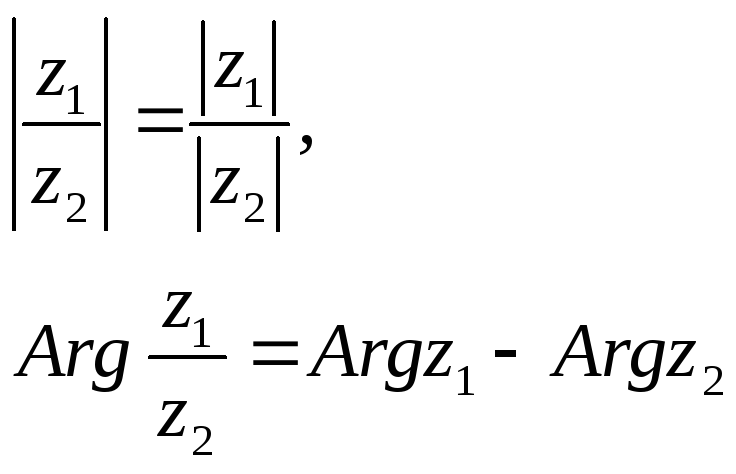(2.86)

Используя эти правила, можно значительно упростить определение модуля АФХ. Например, для АФХ

, (2.87)

получим

,

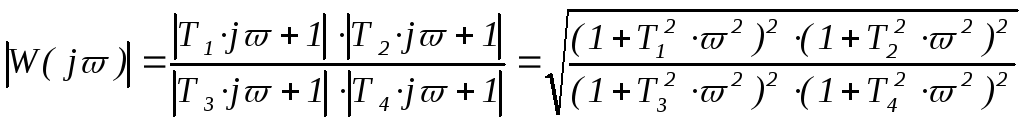(2.88)

,

(2.89)