5.2.4. Обучение приемам выполнения этапов решения

Каждый из этапов процесса решения задачи должен быть вы­полнен с помощью каких-то действий. Если задача при восприятии непонятна, то решающий предпринимает какие-то действия, чтобы превратить ее из непонятной в понятную. Если после того, как со­держание задачи понято, еще не сложился план действий для вы­полнения требования задачи, то решающий также начинает пред­принимать какие-то действия, чтобы найти путь этого выполнения. И так до тех пор, пока задача не будет решена, или пока не станет ясно, почему требование не может быть выполнено. Поэтому, сколько люди решают задачи, столько они ищут ту совокупность или после­довательность действий, выполняя которую они могли бы от задачи перейти к выполненному требованию в соответствии с условием за­дач. Для чисто математических задач результатом этого поиска стали алгоритмы решений многих классов задач.

Ранее отмечалось, что долгое время обучение решению текстовых задач велось как организованное и ведомое учителем решение задач на уроках. В этот период были разработаны такие приемы, примене­ние которых учителем или под его руководством учащимися, обеспе­чивало понимание учащимися задачи, делало успешным ее решение. В результате к началу 80-х годов ХХ в. в методической литературе на­копилось большое количество таких приемов¹. В это же время были разработаны приемы работы с решенной задачей², решение тексто­вых задач с применением рисунков, схем, чертежей³.

¹ Бантова М.А. Методика преподавания математики в начальных классах / М. А. Бантова, Г. В. Бельтюкова, А. М. Полевщикова. — М., 1984.

² Там же.

³ Левенберг Л. Ш. Вопросы использования графических изображений при решении математических задач в начальной школе // Автореф. дисс. на соиск. ученой степени канд. пед. наук. — Ташкент, 1975; Левенберг Л. Ш. Рисунки, схе­ мы и чертежи в начальном курсе математики. — М., 1978.

218

Осознав далее и разделив понятия обучения решению задач и ре­шения задач на уроке, пришли к выводу, что приемы работы с за­дачами — это приемы выполнения этапов решения, которым можно специально обучать детей, которые могут и должны войти в содер­жание обучения. Приемы были собраны, включены в содержание обучения. В настоящее время обучение таким приемам, равно как и знаниям о них, о задачах, процессе решения задач — это выпол­нение требований ФГОС НОО. Современные учебники содержат соответствующий учебный материал.

Методические подходы к обучению приемам, помогающим выполнению этапов решения. Эффективным является методиче­ский подход, предусматривающий опору на имеющийся у учащихся опыт интуитивного применения многих приемов, помогающих реше­нию, обогащение этого опыта, проведение специальных уроков озна­комления с приемами (темы: «Рисунки при решении задач», «Учимся делать краткую запись задачи», «Учимся работать с текстом задачи», «Учимся представлять (драматизировать содержание задачи» и т.п.); организацию специальной деятельности учащихся, направленную на овладение отдельными операциями приема, приемом в целом, на применение осваиваемых приемов в решении задач, указанных учителем и выбранным самостоятельно.

Обучение конкретным приемам выполнения этапов решения, методам и способам решения можно вести по следующей схеме: • накопление учащимися практического опыта применения приема (метода, способа) по указанию учителя и с его помощью; • осозна­ние приема как соответствующей цепочки действий и операций, как «инструмента» для решения; • организация «целостного акта учебной деятельности»¹ учащихся по освоению приема (от принятия каждым ребенком учебной цели «научиться решать задачи с помощью …» или «научиться строить чертеж (рисунок) к задаче», и т.д. до получения каждым ребенком ответа на им же поставленные вопросы: «Научил­ся ли я решать задачи с помощью …?», «Что я уже умею для реше­ния задач с помощью …»; • решение задач с помощью изученного приема, метода, способа, осознание его достоинств и недостатков, границ и особенностей применения.

При введении в процесс обучения приемов (приема), помогаю­щих решению задачи, также как и при введении любого другого со­держания образования, необходимо мотивировать учащихся на его изучение и овладение им.

Методическими средствами, создающими такую мотивацию, осознание необходимости самостоятельного его применения и при­нятие учащимися учебной цели «научиться применять этот прием самостоятельно», могут быть следующие:

¹ Давыдов В. В. Концепция учебной деятельности / В. В.Давыдов, А. К. Мар­кова // Вопросы психологии. — 1981. — № 6.

219

• на конкретной задаче обеспечивается переживание учащимися невозможности решения конкретной задачи, а после применения учителем приема — легкости такого решения, понимание того, что именно прием превратил их из не способных решить задачу в успешных решателей;

• обобщение опыта применения приема при решении задач под руководством учителя.

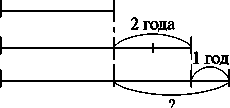
Пример 1. Тема части урока: «Чертеж (геометрическая модель) задачи — помощник при решении задач». Тема записывается после введения. Учитель предлагает учащимся решить задачу, которая без чертежа им не доступна, а после его построения легко решается, напри­мер, такую: «Лена старше Тани на 2 года, но младше Оли на 1 год. Кто старше, Лена или Оля и на сколько лет?» — Кто решил задачу и знает ответ? … — Ответа нет. Повторю еще раз задачу. Слушайте. … (Вновь проговаривает текст задачи, одновременно представляя на доске ее геометрическую модель в виде трех отрезков (рис. 5.4).

— Кто знает ответ на вопрос задачи? (Все учащиеся подняли руки. Они знают ответ на вопрос задачи: «Оля старше Тани на 3 года») — Я удивлена. Когда первый раз прочитала задачу, никто не смог ре­шить задачу, а теперь все решили. Что произошло? Почему вы теперь такие умелые? (Первый раз вы читали задачу без отрезков. А на от­резках видно, кто старше и на сколько!) — Так это мой чертеж сделал вас такими успешными «решателями»?! (Да.) — Если бы вы умели изображать так задачу, то могли бы и сами решать подобные задачи? (Да.) — Хотите научиться строить чертежи к задачам (представлять за­дачи на отрезках? (Да.) — Что вам для этого нужно делать? …

Далее в ходе обсуждения дети решают построить коллективно чер­теж к одной задаче, выделив, что и в какой последовательности де­лать, чтобы содержание задачи представить на отрезках. Результатом этой работы может стать «Памятка»: «Как построить чертеж к задаче». Пункты этой «Памятки»: 1) определить, что изображать отрезками; 2) выбрать, что изобразить отрезком в первую очередь, как расположить этот отрезок, какой длины его чертить; 3) начертить отрезок, сделать пометки, записи, чтобы было ясно, что обозначено отрезком. Возвра­титься к шагам 2) и 3), выполнить их относительно части задачи, еще не представленной на отрезках; … И так до тех пор, пока вся задача не будет представлена на отрезках.

Таня

Лена Оля

Пример 2. При обобщении опыта применения приема постановки спе­ циальных вопросов по тексту задач, после решения нескольких задач с уча­ стием учителя, где был применен на­ меченный к изучению прием, учитель организует беседу. — Обратили ли вы Рис. 5.4 внимание на то, что при коллективном

220

решении задач, я задаю вам много вопросов, на которые вы отвечае­те и находите решение? (Да.) — Какие вопросы я задаю? (О чем эта задача? Что требуется узнать? Что известно, про то о чем спрашивает­ся? …). — Могли бы вы сами задавать такие вопросы? (Да.) — Как вы считаете, полезно ли научиться задавать вопросы? (Да.) Вместе с уча­щимися определяем, какие могут быть вопросы и каких ответов на них следует ожидать. После чего можно организовать работу в парах: один учащийся задает вопросы по тексту задачи, другой отвечает, затем уча­щиеся меняются ролями.

Аналогично может быть организована работа и с другими приема­ми. Приемы и их характеристика представлены далее.

Восприятие и осмысление задач (табл. 5.2). Правильное чте­ние или слушание задачи (прочтение всех слов и предложений, в том числе математических — чисел, математических выражений, равенств и неравенств, математических терминов, расстановка логических ударений) является первым шагом к ее пониманию. Обучение пра­вильному чтению особенно актуально в первом классе.

Пусть вопрос некоторой сюжетной текстовой задачи таков: «Сколько учебников на книжной полке?» Условию задачи соответ­ствует лишь один вариант логического ударения при чтении вопроса. Вне текста задачи этот вопрос имеет пять вариантов (по количеству

Таблица 5.2

Назначение Приемы выполнения Критерии овладения

Понять задачу: о чем задача, что требуется узнать, построить, обосновать; о чем спрашивается, что из­вестно, что неизвест­но; что означает каж­дое слово,словосоче­тание, число; выявить отношения, связи между данными, дан­ными и неизвестны­ми, данными и иско­мым

Правильное чтение и слушание задачи. Представление, дра­матизация ситуации задачи. Постановка специ­альных вопросов по тексту задачи. Разбиение текста задачи на смысловые части. Переформулировка текста задачи. Построение вспомо­гательной модели (предметная, рису­нок, краткая запись, таблица, схема, чер­теж, график, диа­грамма

Решающий: • выделя­ет в задаче условие и требование; • пред­ставляет ситуацию за­дачи и себя участни­ком или наблюдате­лем; • ставит вопросы по тексту и отвечает на них; • представляет содержание задачи разными средствами (другими словами, на предметах, в ри­сунке, на чертеже и т.д.); • называет от­ношения (что (чего) больше, меньше, на (в) сколько, что чему равно, что является частью чего и т. п.)

221

слов) постановки логического ударения. Прочитаем вопрос с разным логическим ударением. Выделение слова «сколько» будет означать, что условие задачи содержит информацию не только о количестве, но и о каких-то других характеристиках учебников на книжной пол­ке. Ударение на слове «учебников» сообщает, что кроме учебников на полке было еще что-то, на предлоге «на» — что учебники могли быть также под полкой, у полки; на слове «книжной» — что учебни­ки находятся не только на книжной, но и на какой-то другой полке, на слове «полке» — что учебники находятся не только на полке. При чтении текста задачи лишь один вариант логического ударения будет помогать пониманию.

Восприятию задачи на слух помогает создание специального на­строя на слушание, выработка вместе с детьми рекомендаций, вы­полнение специальных заданий на прочтение и анализ прочтения задачи кем-то. Обучение приемами этой группы — это обучение универсальными учебными действиями по работе с текстом в соот­ветствии с ФГОС НОО. Богатым потенциалом для выполнения этих требований обладает обучение решению текстовых задач.

Представление ситуации задачи — это мысленное рисование картинок (зрительных образов), которые могут сопровождаться зву­ковыми, осязательными, кинестетическими ощущениями.

При чтении или слушании задачи зрительные образы возника­ют и без специальных усилий. Однако спонтанное представление задачной ситуации может привести к возникновению образов, за­трудняющих понимание. Например, представление халатов и платьев при знакомстве с задачей «Швейная фабрика шила халаты и платья. На одно платье шло 3 м ткани, а на один халат 4 м. Сколько халатов и сколько платьев сшито из 924 м, если платьев и халатов было по­ровну?» будет только мешать пониманию и выбору арифметических действий. Если же представим частично раскатанный рулон ткани, на которой стоят метки через каждые 3 и 4 м (на платье, на халат и т.д.) то задача становится не только понятной, но и почти решен­ной (рис. 5.5).

Драматизация задачи — представление себя участником ситуа­ции задачи, мысленное или реальное ее проигрывание. Этот прием является развитием предыдущего. Для сюжетной задачи драматиза­ция заключается в проигрывании сюжета. Более сложно, но не менее интересно «драматизировать» чисто математические задачи, в част­ности задачи на открытие, изобретение способа действий.

Зм 4м Зм 4м Зм 4м ... Зм 4м

1 пл.|	1х.	]1 пл.[	1х.	|1пл.| ...		|1пл.|	1х. |
».							1

924 м

Рис. 5.5

222

Покажем два вида драматизации (предметный и «оживление») на примере задачи на изобретение вычислительного приема.

Задача. Как вычитать «в столбик» в случаях вида 2 000 - 768?

Условие задачи: случаи вычитания вида 2 000 - 768. Требование: разработать способ вычитания. Задача может быть предложена детям до знакомства с соответствующим вычислительным приемом, но после вычитания «в столбик» в более простых случаях. Способы драматиза­ции предлагает учитель.

Предметный. Представим: мы работаем в оптовом магазине, в ко­тором есть 2 000 шт. тетрадей. Они упакованы так: 2 упаковки по 1 000 штук, каждая из которых составлена из 10 пачек по 100 штук, а каж­дая пачка — из 10 упаковок по 10 штук. (Материализовать этот образ можно в виде двух наборов по 10 квадратов 10 × 10 см). Покупателю нужно отгрузить 768 шт. Это 8 отдельных тетрадей, 6 упаковок по 10 шт. и 7 пачек по 100 шт. Но все наши тетради в двух больших упаковках по 1 000 штук!? Что делать? Нужно подготовить тетради для выдачи. Дети предлагают распаковать 1 тыс. Получим 10 пачек по одной сотне. Из 10 возьмем одну «сотенную» пачку. Останется 1 упаковка в 1 тыс. тетрадей и 9 упаковок по 100 шт. А одну «сотенную» упаковку «распаку­ем» и получим 10 упаковок по 10 шт. (нарежем полоски по 10 полосок шириной в 1 см из каждого квадрата). Из этих упаковок возьмем одну и распакуем ее так, чтобы были отдельные тетради (разрежем полоску на 10 квадратов — квадратных сантиметров). В результате 2 000 тетра­дей это 1 тысяча, 9 сотен, 9 десятков и 10 отдельных тетрадей. Теперь вычесть 768 в столбик легко.

«Оживление». Вычитание в столбик поразрядное. Я разряд единиц уменьшаемого. Я должен отдать 8 единиц. Но у меня нет ни одной еди­ ницы! Пойду к соседу — разряду десятков. У соседа тоже пусто, и ему тоже нужно отдавать 6 десятков. Пойду к сотням. И там пусто, а отда­ вать нужно 7 сотен. И только у тысяч не пусто. Хороший разряд тысяч. Дал мне 1 тысячу, но с условием, чтобы я поделился со всеми. Я зашел к сотням — и 1 тысяча превратилась в 10 сотен. Беру себе 1 сотню, 9 со­ тен оставляю и иду к разряду десятков. Сотня превращается в 10 де­ сятков. Беру себе 1 десяток, а 9 оставляю. ₁₉₉₁₀ Иду к себе. Десяток превращается в 10 _2000 2000 2000

единиц. Теперь во всех разрядах не пусто: г—

у тысяч — 1 тысяча, в разряде сотен — 9,

О б в

у десятков — 9, а у меня 10! Теперь мы все справимся с вычитанием (в) (рис. 5.6). Рис. 5.6

Разбиение текста задачи на смысловые части. Применение данного приема способствует как пониманию, так и запоминанию содержания задачи. На разных этапах обучения, для разных задач раз­биение текста задачи учащимися может производиться по-разному.

В текстовых сюжетных задачах может быть полезно разбиение на части, описывающие: начало события; произведенное потом

223

действие с объектами задачи; конечный момент события, результат действия, о чем спрашивается в задаче. (Петя принес 6морковок, | а Катя — 4. | Кроликам отдали 8 морковок. | Сколько морковок осталось?)

В вычислительных задачах на нахождение значения выражения полезно выделить действия в скобках и без скобок, части выражения с умножением и делением. При решении уравнений необходимо вы­деление левой и правой частей равенства. Для некоторых задач важно выделение описаний совокупностей предметов (множеств), величин, их значений и связывающих их отношений.

Обучение этому приему на практике показало, что при решении текстовых задач к нему чаще обращаются дети с низкой техникой чтения, с небольшим объемом внимания. Детям с трудностями в вос­приятии можно рекомендовать закрывать часть текста листом бума­ги. Прочитав, обдумав и обсудив прочитанное, ученик передвигает листок, открывая следующую часть для чтения.

Переформулировка задачи состоит в изложении содержания за­дачи по-другому. Переформулировка — мощное средство понимания и представления смысла прочитанного, средство развития устной и письменной речи во всех ее видах. Умение пересказать текст по-другому, выразить его содержание другими языковыми и графически­ми средствами — показатель и двигатель интеллектуального развития. Развивается оно вместе с развитием устной и письменной речи.

Переформулировка текстовой задачи может быть разной: замена термина содержательным описанием, содержательного описания — термином, некоторых слов — синонимами; исключение части тек­ста, не влияющей на результат решения; изменение порядка слов и (или) предложений; дополнение текста пояснениями; замена число­вых данных другими, более наглядными с последующим переносом их смыслов на реальные числовые данные задачи; замена числовых данных буквенными или буквенных данных числовыми; введение других, удобных единиц величин и другие изменения текста.

Задача. За 35 тетрадей уплатили 70 р. Сколько нужно уплатить за 16 блокнотов, если блокнот на 8 р. дороже тетради? Переформулирован­ный текст: «Стоимость всех тетрадей — 70 р., количество тетра­дей — 35, цена неизвестна». (Первая часть задачи.) «Стоимость всех блокнотов неизвестна — ее нужно найти. Количество блокнотов — 16, цена неизвестна». (Вторая часть). «Цена блокнота на 8 р. больше цены тетради». (Третья часть). Затем выстраиваем информацию в логике «цена — количество — стоимость»: «Цена тетради — неизвестна, количество — 35 шт., стоимость — 70 р. Цена блокнота — на 8 р. больше цены тетради, количество блокнотов — 16, стоимость нуж­но найти».

Переформулировка задачи может быть выполнена устно или пред­ставлена в записи. Записью переформулированного текста задачи

224

может быть ее краткая запись, в которой информация об объектах задачи и их отношениях задается словами, числами, графическими символами, линиями, особым образом расположенными на листе бумаги. Умение записать содержание текста кратко есть универ­сальное учебное действие. Образцы кратких записей представлены в учебнике математики (Стойлова Л. П. Математика. — М., 2012). Некоторые формы будут рассмотрены далее.

Критерием оценки качества краткой записи текстовой задачи, как и любой записи в процессе обучения, является степень соответ­ствия записи ее назначению — той цели, ради достижения которой она выполняется. Главное назначение краткой записи при решении задачи — сделать задачу понятнее, «визуализировать» отношения за­дачи. Необходимость краткой записи в работе с конкретной задачей на уроке должна определяться ее ролью в достижении планируемых результатов. Чтобы обучение помогало детям понять мир и себя, не­обходимо обсуждать с ними вопросы назначения и места записей, развернутых, «длинных» и свернутых, кратких, в жизни человека и общества, в обучении, в изучении чего-либо, в изучении матема­тики, в решении задач, в овладении умениями решать задачи.

Отметим, что в первом классе детям легче решить текстовую за­дачу, чем записать ее кратко. Это вполне объяснимо. Решить зада­чу — значит ответить на ее вопрос. Опыт ответов на вопросы у перво­классников велик: с трех-четырех лет дети каждодневно задают во­просы и отвечают на них. А овладевать письмом и письменной речью, умением передавать содержание текста кратко они только начинают. И потому нужно специальное и грамотное обучение этому умению.

Переформулировка может также заключаться во введении удобных единиц измерения величин, которые не только помогают понять зада­чу, но и задают метод решения, который мы назвали физическим.

Задача. Из пункта А в пункт Б отправился пешеход. Через 2 ч из пун­кта А в том же направлении отправляется велосипедист, скорость ко­торого в три раза больше скорости пешехода. Сколько времени пона­добится велосипедисту, чтобы догнать пешехода?

Трудность понимания этой задачи в том, что не даны значения длины пути и скорости. Чтобы получить их, введем «свою» единицу длины. За единицу удобно взять длину пути, пройденного пешеходом за 1ч. Назовем ее, например, «пеш». Тогда длина пути, пройденного пешеходом за 1 ч равна 1 пеш, а скорость пешехода — 1 пеш/ч. С уче­том введенных обозначений переформулируем текст задачи: из пун­кта А в пункт Б отправился пешеход со скоростью 1 пеш/ч. Через 2 ч из пункта А в том же направлении отправляется велосипедист, скорость которого в три раза больше скорости пешехода. Сколько времени по­надобится велосипедисту, чтобы догнать пешехода?

Переформулированная задача — стандартная задача на движение.. Известна скорость пешехода, легко находятся скорость велосипедиста —

225

3 пеш/ч, скорость взаимного движения в одном направлении 3 - 1 = = 2 (пеш/ч). Длина пути, пройденная пешеходом до выезда велосипе­диста — 2 пеш. Искомое время равно 2 ч: 2 пеш : 2 пеш/ч = 2 ч.

Построение модели задачи. «Модель (в широком понимании) — образ (в том числе условный или мысленный — изображение, схема, чертеж, график, план, карта и т. п.) или прообраз (образец) какого-либо объекта или системы объектов (оригинала данной модели), ис­пользуемой при определенных условиях в качестве их «заместителя» или «представителя» … Модель может быть системой более высокого уровня абстракции, чем ее оригинал, … и более низкого»¹.

Процесс математического решения любой текстовой сюжет­ной задачи состоит из трех частей: а) построение математической модели текстовой задачи (числового выражения или последователь­ности числовых выражений, уравнения, неравенства и т.п.); б) ре­шение задачи на языке математической модели — решение чисто математической задачи; в) интерпретация решения математи­ческой задачи на языке текстовой задачи.

Математической моделью задачи называют составленные по за­даче математическое выражение, уравнение или неравенство, логи­ческая последовательность суждений при логическом решении, гео­метрические фигуры и построения при геометрическом решении.

Вспомогательные модели используются для визуализации и структурирования содержания задачи. Они помогают увидеть и по­нять отношения, установить зависимости и на этой основе построить математическую модель. Следующие вспомогательные модели задач могут помочь решающему на этапе восприятия и осмысления задачи: предметная; условно-предметная (рисунок); графическая (постро­ение графика в некоторой системе координат); геометрическая (чертеж); словесно-графическая модель (краткая запись).

Задача. В конкурсе чтецов мальчиков участвовало на 3 меньше, чем девочек. Сколько всего участников конкурса, если девочек 9?

Предметная модель. а) С использованием приема драматиза­ции. Выходят 9 девочек. В пару с каждой девочкой, кроме трех, ста­вится мальчик. (Каждой девочке в пару становится мальчик, затем 3 мальчика уходят. б) Выкладываем 9 треугольников — это девочки; выкладываем 9 квадратов — это столько же мальчиков, сколько и де­вочек. Чтобы мальчиков стало на 3 меньше, 3 квадрата убираем.

Условно-предметная модель — это рис. 5.7.

Графическая модель — построение графика в некоторой системе координат, например линейной (рис. 5.8).

Геометрическая модель — представление содержания задачи с по­мощью геометрических фигур и их свойств (рис. 5.9).

¹ Большая советская энциклопедия. — М., 1974. — С. 399.

226

Словесно-графическая модель — краткая запись. Примеры даны на рис. 5.10.

ААААААААА АААААА

_{ПППППП00И □□□□□□}

AAA

Рис. 5.7

О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

123456789

3 2 10

Рис. 5.8

У"!

? б

Рис. 5.9

М. — ?, на 3 меньше, чем Д. , „ Д--9. ^^?

м	?, на 3 меньше
Д	9
Всего	?

	Меньше М	На сколько	Больше Б	Зависимости	Всего М + Б = Всего
Обобщение	а	А		а - а = п П - А = П П - П = А	а + □ =0
Задача	?	3	9	П - А = О. а - П = 0	?9-3 = 6 6-9=15

Рис. 5.10

227

Учимся решать задачи

®

Прочитай задачу. Подчеркни условие и требование задачи разными цветами.

В гараже было 20 машин. Затем приехало еще 40 машин. Сколько машин стало в гараже?

Рассмотри схемы в задаче. 7

20 маш., 40 маш.

20 + 40

Реши задачу. Вычисли ответ.

Рис. 5.11

Далее показаны два вида оригинальных моделей¹: первая «вышла» из представления задачи на отрезках, но не требует измерения длин; вторая — «это диаграмма Эйлера— Венна, состоящая из двух кругов, один из которых находится внутри другого»² (рис. 5.11).

Постановка специальных вопросов по тексту задачи. Когда мы чего-либо не понимаем, мы задаем вопросы. Умение ставить вопро­сы — важное умение в любой сфере деятельности. Не зря говорят: «Хорошо поставленный вопрос — это наполовину и ответ».

Основные вопросы по текстовой задаче могут быть такими: • О чем задача? Что требуется узнать (доказать, найти)? • Что из­вестно (о том, о чем спрашивается в задаче)? • Что неизвестно? • Ка­кие предметы (понятия, объекты) описываются в задаче? • Какими свойствами, величинами они характеризуются? • Что обозначают слова …, числа …, словосочетания …? Постановка вопросов — это универсальное учебное действие, компонент общего умения решать задачи. Чтобы отношение к тексту «с вопрошанием» стало привыч­кой, учащиеся должны иметь возможность задавать вопросы по лю­бой задаче.