Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

математика

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

403.1 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Задание № 3. Проверить компланарность векторов																						a , b , c .
a 7, 4, 6 , b 2, 1, 1 , c 19, 11, 17 .
Векторы a , b , c											компланарны, если их смешанное произ-
ведение равно нулю.
							7		4		6			1	1		2	1			2	1


						2 1					1	7				4			6
a b		c				2 1					1	7		11	17	4	19	17	6	19		11
						19		11		17				11	17		19	17		19		11
						19		11		17
= 7(17 11) 4(34 19) 6(22 19) 42 60 18 0 .
Следовательно, a , b , c компланарны.
Задание № 4. Написать разложение вектора x																					по векторам
p , q , r . x 15, 20, 1 ,													p 0, 2, 1 , q 0, 1, 1 , r 5, 3, 2 .
Представим вектор													x в виде линейной комбинации векто-
ров p , q , r :											x 1 p 2 q 3 r .
											x 1 p 2 q 3 r .
Запишем это векторное уравнение в проекциях на оси OX,
OY, OZ.
15 1 0 2 0 3 5,

20 1 2 2 1 3 ( 3),
1 1 ( 1) 2.
				1					2				3
Решим систему уравнений относительно 1, 2 , 3 .
5			15,
	3						3 3 20,
2 1 2							3 3 20,
					2				1.
				2	2				1.
	1			2			3
3	3.						Найдем					сумму			2-ого		и	3-его			уравнений
3 1 3	21,						3 1 21 3 18, 1 6 . Подставим															1 6,
3 3 во 2-ое уравнение:													2 ( 6) 2 3 3 20, 2							1.
Следовательно, x 6 p q 3r .
Задание № 5.Даны четыре точки в																	трехмерном				пространст-

ве

A , B , C , Д . Показать, что они могут являться вершинами пирамиды. Найти: а) объем пирамиды; б) уравнение плоскости

АВС ; в) длину ребра АД ; г) угол между ребром АД и гранью АВС ; д) площадь грани АВД .

Пусть A1 , B1 , C1 есть проекции точек A , B , C на плоскость x0 y . Найти: е) длину высоты A1K ; ж) угол между высотой

A1K и медианой A1N треугольника A1B1C1.
Пример.		Даны четыре	точки	A 1, 0, 2 , B 2, 3, 4 ,
C 0, 1, 1 , D 3, 0, 2 . Покажем,			что эти точки		могут являться
вершинами	пирамиды. Составим три вектора				AB 1, 3, 2 ,
AC 1, 1,	3 ,	AD 2, 0, 4 . Проверим		условие компланар-

ности этих трех векторов. Составим определитель из координат векторов

1	3	2	1	3		1	3		1	1

1	1	3			3			2			( 4 0)
			0	4		2	4		2	0
2	0	4

3 (4 2 3) 2 (0 2) 4 30 4 22.

Так как определитель отличен от нуля, то векторы не лежат

в одной плоскости и точки					A, B ,C , D могут являться вершинами
пирамиды.
Найдем а) объем этой пирамиды.
V	1	1	3	2		22		11

		1	1	3					(куб. ед.).

6		2	0	4	6		3

Найдем б) уравнение плоскости ABC . Воспользуемся уравнением плоскости, проходящей через три заданные точки

x 1		y 0		z 2					x 1 y				z 2
2 1	3 0			4 2		0			1		3		2		0
0 1		1 0	1 2						1	1				3
(x 1)		3	2	y	1		2	(z 2)			1	3		0
		3	2		1		2				1	3
		1	3		1		3				1		1
		1	3		1		3				1		1

(x 1)(9 2) y( 3 2) (z 2)(1 3) 0

7(x 1) y 2(z 2) 0, 7x 8 y 2z 4 0,

7x y 2z 3 0 .

Найдем в) длину ребра AD .

AD 22 02 ( 4)2 4 16 20 25 .

Найдем г) угол между ребром AB и гранью ABC .

Угол между ребром AD и гранью ABC находится через угол между вектором AD и вектором N , перпендикулярным

плоскости ABC . 900													.
Вектор N 7, 1, 2 перпендикулярен ABC .
cos cos(900											) sin								AD N
cos cos(900											) sin
																			AD			N
				2 7 0 1 ( 4) ( 2)																					14 8						22			0,67
																																		0,67
	22 02 ( 4)2													72 12 ( 2)2											20		54			32,862
sin 0,67 42,0250 .																			ABD . Площадь
Найдем					д) площадь грани														ABD . Площадь											треугольника
			1
ABD равна			1			AB AD						. Найдем векторное произведение векто-
ABD равна						AB AD						. Найдем векторное произведение векто-
		2
		2
ров AB и AD
							i				j			k				3			2					1 2						1	3
							i				j			k				3			2					1 2						1	3
AB AD							1				3			2	i				0		4		j			2	4			k		2	0
							2				0		4						0		4					2	4					2	0
							2				0		4

i (12 0)										( 4 4) k (0 3 2) 12i														8 j 6k .
i (12 0)									j	( 4 4) k (0 3 2) 12i														8 j 6k .
				1													1											1	15,6 7,81.
S ABD								122 82					62
																				144 64 36
																				144 64 36
		2														2											2
A1(1, 0) ,					B1(2, 3) ,								C1(0, 1) – проекции точек																	A,	B ,		C на
плоскость XOY .
Найдем е) длину высоты A1K .

Напишем уравнение прямой B1C1 и найдем расстояние от точки A1 до прямой B1C1 .

	B C :	x 2			y 3				x 2						y 3
	B C :
	1 1 0 2				1 3						2			4
2(x 2) ( y 3), 2x 4 y 3
	B1C1 : 2x y 1 0
	A K		2 1 0 1					1				.





	1			22 12				5
				22 12				5
Найдем ж) угол между высотой A1K и медианой A1M тре-
угольника A1B1C1.																			N 2, 1 , перпендику-
Вектор A1K коллинеарен вектору																			N 2, 1 , перпендику-
лярному прямой B1C1 . Найдем координаты точки M , которая яв-
ляется серединой B1C1 .													xB	xC				2 0
													xB	xC				2 0
							xM						1	1						1
							xM							2					2	1
														2					2
										yB yC							3 1
						yM							1		1					1.
						yM							2			2				1.
Найдем													координаты							вектора

A1M 1 1, 1 0 A1M 0, 1 .

Угол 1 между высотой A1K и медианой A1M будем определять через векторы N 2, 1 и A1M 0, 1 .

cos 1 0,447, 1 1160 .

Прямые А1К и А1М образуют между собой два угла, которые в сумме составляют 1800 .Так как угол между высотой и медианой не может быть больше 900 , то 1 1800 1160 640 .

Задание № 6. Написать канонические уравнения прямой l в пространстве по заданным общим уравнениям

x 2 y z 3 0,

l :

x y 5z 6 0.

Найдем координаты точки, которая лежит на прямой l . Придадим переменной x произвольное значение, например x 0.

Тогда, подставив x 0 в уравнения прямой l , получим систему линейных уравнений относительно y, z .

2 y z 3,

y 5z 6. Решим систему: y 5z 6

2(5z 6) z 3, 10z 12 z 3, 11z 9, z 9 .

	9		45		21					11
y 5	9	6	45	6	21	.
y 5		6	11	6		.
11			11	11			9		21
							9		21
Следовательно, точка M 0,								,		l .
Следовательно, точка M 0,							11	,	11	l .
							11		11

Найдем теперь

вектор

S ,

параллельный

прямой l .

S N1 N2 , где N1

1, 2, 1 , N2

1, 1, 5 векторы нормали для

плоскостей, в пересечении которых получается прямая l .

2 1

S N1 N2

11i 6 j k

Запишем теперь канонические уравнения прямой:

x 0

11		6	1
	x	11y 9	11z 21	.
		66
	11		11

Задание № 7. Найти точку пересечения прямой и плоскости. Прямая задана каноническими уравнениями

x 2 y 1 z 1 . 3 2 5

Перейдем к параметрическим уравнениям прямой:

x 3t 2,

y 2t 1,z 5t 1.

Подставим x(t) , y(t) , z(t) в уравнение плоскости x 2 y z 7 0:

3t 2 2(2t 1) (5t 1) 7 0 3t 2 4t 2 5t 1 7 0

2t 6 0, t 3.

Найдем координаты точки пересечения x 3 3 2 7,

y 2 3 1 7, z 5 3 1 14.


Задание № 8. Найти точку		M , симметричную точке
M ( 1, 0, 3) относительно прямой	x 3		y 5	z	.

	5	2		1

Вектор S 5, 2, 1 параллелен прямой. Напишем уравнение плоскости, проходящей через точку M и перпендикулярной вектору S .

5(x ( 1)) 2( y 0) (z 3) 0 5(x 1) 2 y z 3 0

5x 5 2 y z 3 0 5x 2 y z 8 0 .

Найдем точку A пересечения прямой и полученной плоско-

сти.

Найдем параметрические уравнения прямой и подставим в уравнение плоскости

x 3 y 5 z t

5 2 1

x 5t 3,

y 2t 5,z t.

5(5t 3) 2(2t 5) ( t) 8 0, 25t 15 4t 10 t 8 0 ,

30t 13,

t 13 . 30

				13										65 90									25					5
x 5											3																			,
x 5				30							3					30														,
				30												30							30					6
				13											26 150									176
y 2												5																			,
y 2												5				30															,
				30												30								30
z	13	.
z		.
30					5							176				13
					5							176				13
Точка			A						,						,							является							серединой
Точка			A						,		30				,	30						является							серединой								отрезка M M .
					6						30					30											.

Найдем координаты точки M x , y																								, z
								x ( 1)									5		,			y 0				176							,	z 3				13	.
																			,				2										,	2					.
											2					6							2					30						2			30
		x				10						1			16					8	,		y		176							, z			13	3				32	.
		x										1			6						,		y									, z				3					.
							6								6			3						15										15			15
			13							176						32
							,						,							.

Т.е. M				30							15					15
				30							15					15

Задание № 9. Определить тип кривой второго порядка по общему уравнению 4x2 9 y2 32x 54 y 109 0 .

Соберем слагаемые с переменной x и переменной y (4x2 32x) (9 y2 54 y) 109 0

Вынесем за скобки коэффициент при								x2 и y2 , дополним
выражение в скобках до полного квадрата
4(x2 8x 42 42 ) 9( y2 6 y 32								32 ) 109 0
4(x 4)2 64 9( y 3)2 81 109 0
	4(x 4)2 9( y 3)2					36
Поделим обе части уравнения на 36:
	4(x 4)2		9( y 3)2				36

36			36				36
36			36				36
		(x 4)2		( y 3)2
					1 .
9			4		1 .
9			4

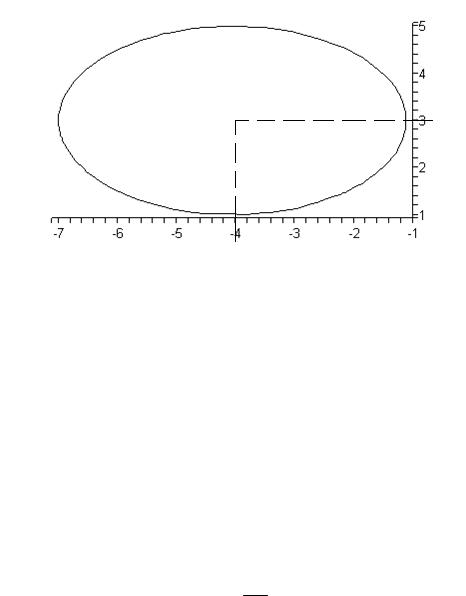
Это каноническое уравнение эллипса с центром в точке O 4, 3 и полуосями a 3, b 2 .

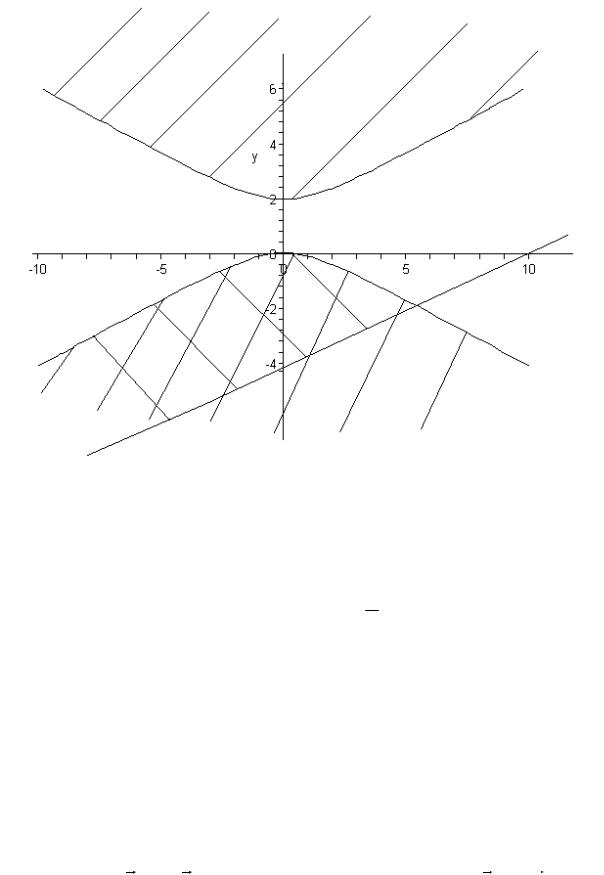
Задание № 10. Построить область решения системы неравенств

4 y2 8 y x2		0,

x	5 y 0.


2

Заменим знак неравенства на равно и определим тип кривой в первом выражении системы.

4 y2 8y x2 0

4( y2 2 y 1 1) x2 0 4( y 1)2 x2 4

( y 1)2 x2 1 . 4

Это каноническое уравнение гиперболы с центром в точке O 0, 1 и полуосями a 2, b 1. Построим эту линию

Неравенство 4 y2 8y x2 0 определяет множество точек, лежащих внутри гиперболы. Подставим в неравенство координаты точки A 0, 1 , 4 8 0 4 0 – это неверно. Следовательно, неравенству удовлетворяют точки, лежащие по другую сторону от

линии относительно точки А. y 0, y x 5 – это прямые линии. 2

Неравенство y 0 определяет множество точек, лежащих ниже


прямой y 0,	y		x		5 определяет множество точек, лежащих

	2
выше прямой	y	x		5 . Область, обозначенная двойной штри-

	2

ховкой является решением системы неравенств.

Задачи для самостоятельной работы

Задача № 1. Вычислить площадь параллелограмма, построенного на векторах а и b , если угол между векторами p и g равен


1.1	a p 2g ,	b 3 p g ;		p								1 ,								g							2 ,													.


																																				6
																																				6
																																								.
1.2	a 3 p g ,	b p 2g ;		p								4 ,									g							1 ,
1.2	a 3 p g ,	b p 2g ;		p								4 ,									g							1 ,
																	1																			4
	a p 3g ,	b p 2g ;					p																	g												4
1.3																		,															1 ,															.


														5																						2
														5																						2
1.4	a 3 p 2g ,	b p 5g ;						p								4 ,							g											1	,						5											.
																																		1							5

																														2						6
																														2						6
1.5	a p 2g ,	b 2 p g ;			p								2 ,								g								3 ,								3									.
																																					3

																																				4
																																				4
																																																	.
1.6	a p 3g ,	b p 2g ;					p								2 ,								g										3 ,
1.6	a p 3g ,	b p 2g ;					p								2 ,								g										3 ,
																																				3
																																				3
																																																	.
1.7	a 2 p g ,	b p 3g ;					p								3 ,								g									2 ,
1.7	a 2 p g ,	b p 3g ;					p								3 ,								g									2 ,
																																				2
																																				2
																																						.
1.8	a 4 p g ,	b p g ;	p					7 ,											g				2 ,
1.8	a 4 p g ,	b p g ;	p					7 ,											g				2 ,
																																				4
																																				4
																																								.
1.9	a p 4g ,	b 3 p g ;		p								1 ,								g					2 ,
1.9	a p 4g ,	b 3 p g ;		p								1 ,								g					2 ,
																																				6
																																				6
1.10 a p 4g ,		b 2 p g ;					p						7 ,									g							2 ,															.


																																				3
																																				3
1.11 a 3 p 2g ,		b p g ;				p					10 ,														g								1 ,												.


																																				2
																																				2
																																							.
1.12 a 4 p g ,		b p g ;		p					5 ,											g					4 ,
1.12 a 4 p g ,		b p g ;		p					5 ,											g					4 ,
1.13 a 2 p 3g ,		b p 2g ;								p																	g									4
																																				4
																6 ,																	7 ,																		.


																																				3
																																				3
																																											.
1.14 a 3 p g ,		b p 2g ;				p					3 ,											g					4 ,
1.14 a 3 p g ,		b p 2g ;				p					3 ,											g					4 ,
																																				3
																																				3
																																																		.
1.15 a 2 p 3g ,		b p 2g ;								p						2 ,											g						3 ,
1.15 a 2 p 3g ,		b p 2g ;								p						2 ,											g						3 ,
																																				4
																																				4
1.16 a 2 p 3g ,		b 3 p g ;								p					4 ,											g					1 ,																.


																																				6
																																				6
																																										.
1.17 a 5 p g ,		b p 3g ;				p				1 ,											g				2 ,
1.17 a 5 p g ,		b p 3g ;				p				1 ,											g				2 ,
																																				3
																																				3

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015695.77 Кб50Математика для инженеров.pdf
#
10.05.2015298.16 Кб15математика контр раб №2.pdf
#
10.05.20151.05 Mб21Математика МУ к КР ЗФО 24.04.pdf
#
10.05.20152.69 Mб5Математика Сам раб 140400 140100.pdf
#
16.03.2016830.37 Кб3Математика.pdf
#
10.05.2015403.1 Кб4математика.pdf
#
16.03.2016429.54 Кб6Математика.pdf
#
23.11.20191.69 Mб16Математическая обработка геодезических измерени...doc
#
26.08.2019219.14 Кб0Материал для контрольной работы (теория).doc
#
16.03.2016167.91 Кб14материаловедение MU_k_k/r.pdf
#
10.05.2015489.06 Кб39Материаловедение- Контрольные задания.pdf