
Prezentatsia_IG_KhN_KhO_KhP_KhM_2013
.pdf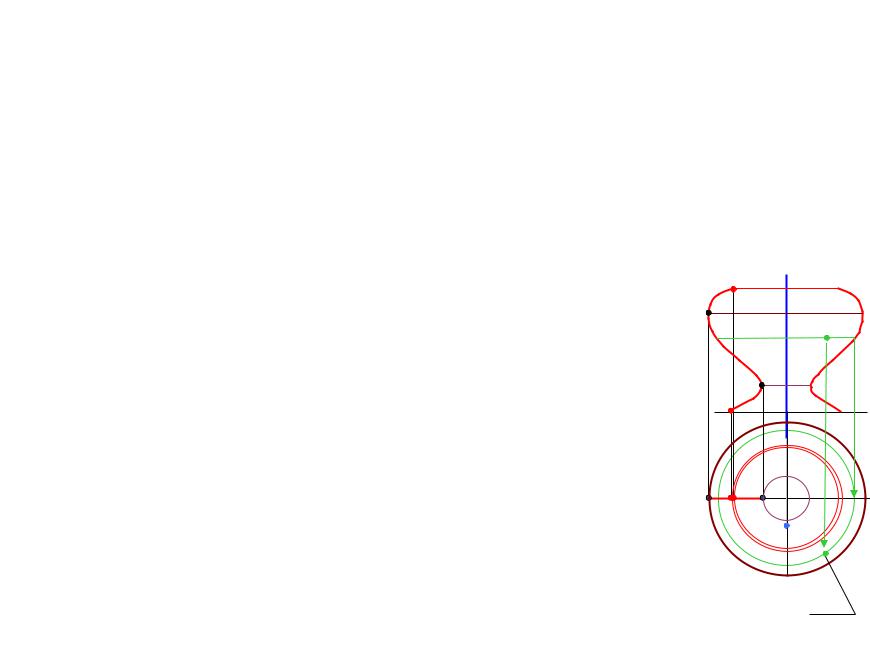
|
|
|
3. Точки и линии на поверхности |
|
|
|
||||||
|
Так как грани многогранника представлѐят собой плоскости, а ребра – прѐмые линии, |
|||||||||||
то построение точек и линий на поверхности многогранника осуществлѐетсѐ на основе |
||||||||||||
свойства принадлежности точки и линии плоскости (см. слайд № 36), и точки – прѐмой (см. |
||||||||||||
слайд № 27). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Поверхности вращениѐ образуятсѐ вращением образуящей ℓ (прѐмаѐ или криваѐ) |
|||||||||||
вокруг оси ί. Ось ί - прѐмаѐ, вокруг которой вращаетсѐ образуящаѐ ℓ . |
|
|
|
|||||||||
|
Окружности, по которым перемещаятсѐ точки образуящей при вращении вокруг оси |
|||||||||||
– параллели поверхности (рис. 6.5). Наибольшаѐ и наименьшаѐ параллели называетсѐ |
||||||||||||
экватором (n) и горлом поверхности (p), соответственно. |
|
|
|
|
||||||||
|
Линии |
поверхности, |
лежащие |
в |
осевых |
плоскостѐх |
l2 |
n2 |
i2 |
|||
|
|
|||||||||||
(т. е. проходѐт через ось вращениѐ) – меридианы. Меридиан, лежащий в |
|
|
||||||||||
|
|
A2 |
||||||||||
П2 – главный меридиан, определѐящий очерк поверхности на П2. На П1 |
|
|
||||||||||
|
|
|
||||||||||
очерк составлѐет горло и экватор. Множество параллелей и меридианов |
|
p2 |
|
|||||||||
– каркас поверхности. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
Если поверхность задана, то можно построить проекции лябой |
x |
|
|
||||||||
|
|
|
|
|||||||||
точки или линии, принадлежит заданной поверхности. |
|
|
p1 |
|||||||||
|
1. Точка принадлежит поверхности, если её проекции |
|
||||||||||
|
l1 |
|
|
|||||||||
принадлежат проекциѐм какой-либо линии поверхности (параллели). |
|
i1 |
|
|||||||||
|
2. Линиѐ принадлежит поверхности, если её проекции проходѐт |
|
|
|||||||||
|
|
|
|
|||||||||
через проекции точек поверхности. |
|
|
|
|
|
n1 |
|
|||||
|
Длѐ построениѐ на чертеже точки, принадлежащей поверхности, |
|
|
(A1) |
||||||||
через неё проводѐт линия, принадлежащуя поверхности. В качестве |
|
|
||||||||||
|
|
|
||||||||||
этой |
линии |
лучше |
использовать |
параллель |
или |
образуящуя |
|
Рис. 6.5 |
81 |
|||
поверхности. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
4. Пересечение поверхностей плоскостья
При пересечении поверхности плоскостья получаетсѐ плоскаѐ фигура, котораѐ называетсѐ сечением.
4.1. Пересечение многогранников плоскостья частного положениѐ
Проекциѐми сечениѐ многогранника плоскостья ѐвлѐетсѐ многоугольник, вершины которого принадлежат ребрам, а стороны – гранѐм многогранника.
Если плоскость занимает проецируящее положение, то проекциѐ сечениѐ (линиѐ) лежит на следе плоскости. Поэтому длѐ построениѐ проекции сечениѐ многогранника плоскостья частного положениѐ достаточно спроецировать точки пересечениѐ следа секущей плоскости с проекциѐми ребер многогранника (рис. 6.6). Особое внимание при этом следует уделѐть установления видимости геометрических элементов (методом конкурируящих точек).
Если проецируящее положение занимаят грани многогранника (прѐмаѐ призма) (рис. 6.7), то одна проекциѐ фигуры сечениѐ совпадает с проекцией самого многогранника и построение сводитсѐ к нахождения недостаящей проекции (по принадлежности точки плоскости).
82

|
S2 |
|
|
ГП2 |
12 |
|
|
|
|
|
|
|
22 |
|
32 |
|
|
|
|
х А2 |
В2 |
|
С2 |
А1 |
|
|
С1 |
|
|
|
|
|
11 |
|
31 |
|
|
|
|
|
S1 |
В1 |
|
|
2 |
1 |
|
|
|
|
|
|
Рис. 6.6 |
|
|
|
|
|
|
|
ТП2 |
|
|
22 |
|
|
|
|
|
|
|
32 |
|
|
1А≡ |
(В ) |
С |
2 |
|
х |
2 2 |
2 |
|
|
|
|
В1 |
≡21 |
|
|
|
|
|
|
|
||
|
А |
|
С |
1 |
≡31 |
|
11≡1 |
|
|
|
ТП1
Рис. 6.7
83

При пересечении поверхности плоскостья общего положениѐ фигура сечениѐ на всех плоскостѐх проекций будет проецироватьсѐ с искажением и длѐ ее нахождениѐ следует применѐть либо методы преобразованиѐ чертежа (длѐ перевода плоскости из общего положениѐ в частное, либо метод секущих плоскостей,
а длѐ многогранников способ рёбер и способ граней.
4.2. Пересечение многогранника плоскостья общего положениѐ
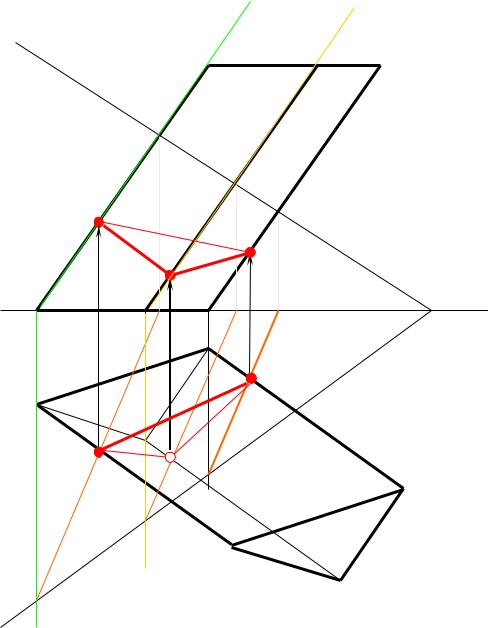
Способ рёбер основан на многократном решении задачи по определения точки пересечениѐ прѐмой с плоскостья (где ребра многогранника - прѐмаѐ) (рис. 6.8).
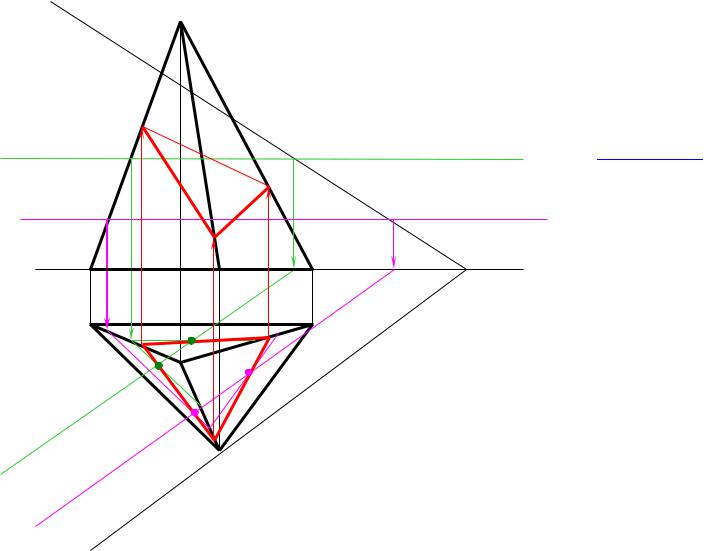
Способ граней основан на многократном решении задачи по определения линии пересечениѐ двух плоскостей (где одна плоскость – грань многогранника) (рис. 6.9).
По количеству геометрических построений эти способы одинаковы и целесообразность применениѐ каждого способа зависит от исходных условий.
84
ГП2 |
|
ТП2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А!2 |
|
|
|
|
|
|
|
М2 |
|
|
|
|
|
|
|
12 |
|
|
Алгоритм решениѐ: |
|||||
3 |
|
I.1. [АА!] ю Т (Т |
|
П ). |
||||
|
|
2 |
┴ |
|||||
|
|
|
|
|
|
2 |
||
|
|
22 |
|
2. Т∩Г= [ЕМ] . |
|
|
||
Е2≡ А2 |
В2 |
|
|
3. [ЕМ] ∩ [АА!] = 1 (на П ). |
||||
С2 |
|
|
|
|
|
1 |
||
|
II. Тоже длѐ других ребер. |
|||||||
х |
М1 |
С1 |
|
|||||
|
|
|
|
|
|
|||
|
|
|
III. |
Соединить |
полученные |
|||
|
|
|
|
|||||
|
|
|
31 |
точки по порѐдку с учетом |
||||
А1 |
(В1) |
|
|
видимости. |
|
|
|
|
|
|
|
|
|
|
|
||
11 |
|
(2 ) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
ТП1 |
|
|
|
|
|
|
|
|
Е1 |
ГП1 |
А!1 |
|
|
|
|
|
|
|
|
Рис. 6.8 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85 |
ГП2 |
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
Алгоритм решениѐ задачи |
||
|
|
|
аналогичен определениѐ линии |
||
|
|
ТП2 |
пересечениѐ |
двух |
плоскостей |
|
|
(см. слайд № 57). |
|
||
А2 |
В2 |
С2 |
|
|
|
х |
|
|
|
|
|
А1 |
|
С1 |
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
В1 |
Рис. 6.9 |
|
|
|
ГП1 |
|
|
|
|
|
|
|
|
|
|
|
86
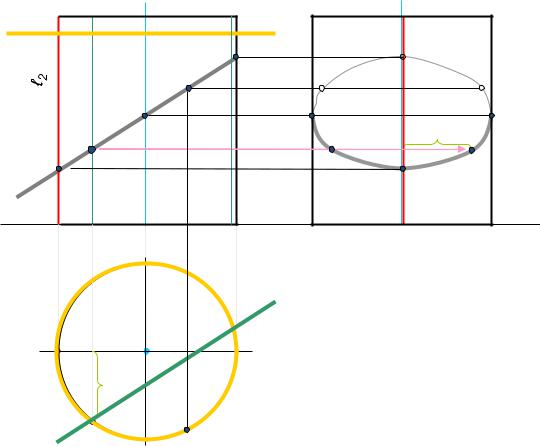
4.3. Пересечение поверхностей вращениѐ плоскостья частного положениѐ |
|||
|
|
а) Прямой круговой цилиндр |
|
|
|
Ф(ℓ, ί) *ί – ось вращениѐ, ℓ – образуящаѐ прѐмаѐ; ℓ ║ί,+. |
|
|
i2 |
i3 |
|
|
RП2 |
|
|
|
|
|
|
|
A2 |
∆y |
A3 |
|
|
||
РП2 |
|
|
|
|
|
ТП1 |
|
l1 |
i1 |
|
|
|
∆y |
Рис. 6.10 |
|
|
|
|
|
|
A1 |
|
|
87
При пересечении поверхности плоскостья получаетсѐ плоскаѐ фигура – сечение.
При пересечении криволинейных поверхностей плоскостья получаетсѐ лекальнаѐ криваѐ. Наиболее часто в технике выполнѐятсѐ сечениѐ цилиндрических и конических поверхностей. Знаѐ возможные виды кривых, которые образуятсѐ по контуру сечениѐ этих поверхностей, можно значительно упростить их построение.
Построение фигуры сечениѐ начинаят с определениѐ опорных (характерных) точек,
лежащих на крайних очерковых образуящих поверхности и определѐящих границы видимости проекций линии сечениѐ, и удаленных на экстремальное расстоѐние от плоскостей проекций.
После определениѐ характерных точек необходимо уточнить фигуру сечениѐ с помощья промежуточных точек.
При пересечении цилиндра плоскостья получаетсѐ :
1. Окружность, если секущаѐ плоскость перпендикулѐрна оси цилиндра
(рис. 6.10, плоскость R).
2. Прѐмоугольник, если секущаѐ плоскость параллельна оси цилиндра
(рис. 6.10, плоскость Т).
3. Эллипс, если секущаѐ плоскость наклонена к оси цилиндра под углом больше 0○, но меньше 90○ (рис. 6.10, плоскость Р).
88
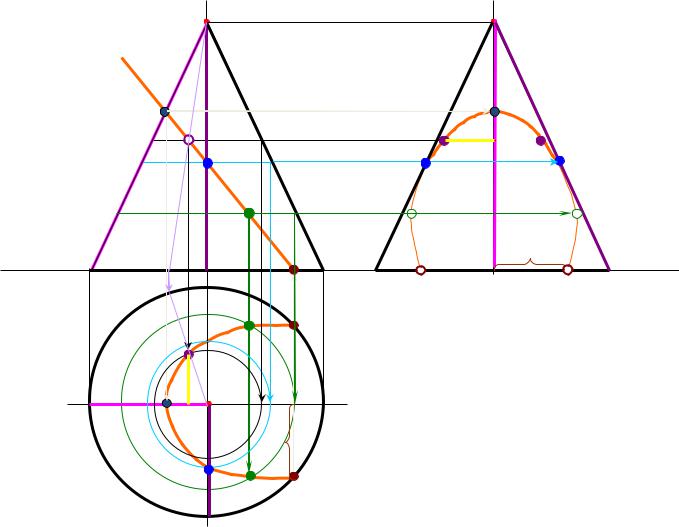
б) прямой круговой конус |
|
|
|
|
|
Ф(ί, ℓ) *ί – ось вращениѐ ,ℓ – образуящаѐ прѐмаѐ; ℓ ∩ ί = S+. |
|||||
i2 |
S2 |
|
|
S3 |
i3 |
РП2 |
|
|
|
|
|
A2 |
|
|
|
A3 |
|
|
|
|
D3 |
|
|
(D2) |
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
C3 |
|
|
|
Е2 |
|
|
(Е3) |
|
|
|
|
|
|
|
|
|
|
B2 |
∆Y |
|
|
|
|
|
|
|
|
|
|
|
(B3) |
D1 |
|
|
|
|
|
A1 |
|
|
|
|
|
I1 = S1 |
|
|
|
|
|
|
|
∆Y |
|
|
|
|
C1 |
Е |
1 |
B1 |
|
|
|
|
|
|
|
|
|
Рис. 6.11 |
89 |
||
|
|
|
|
|
|
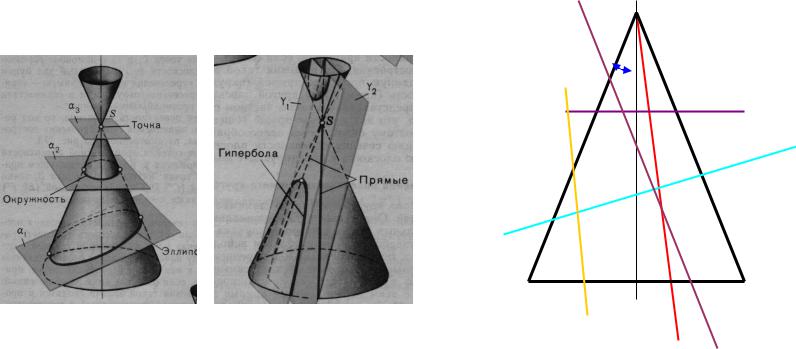
При пересечении прѐмого кругового конуса получаетсѐ:
1.Точка, если секущаѐ плоскость проходит через вершину конуса (рис. 6.12).
2.Прѐмые (образуящие), если секущаѐ плоскость проходит через вершину конуса (плоскость Р).
3. Окружность, |
если |
секущаѐ |
плоскость |
перпендикулѐрна |
оси |
конуса |
(плоскость Т). |
|
|
|
|
|
|
4.Эллипс, если секущаѐ плоскость пересекает ось конуса под углом меньше 90○, но больше угла наклона образуящей конуса к оси (плоскость Г).
5.Парабола, если секущаѐ плоскость пересекает ось конуса под углом, равным углу наклона образуящей конуса (плоскость R).
6.Гипербола, если секущаѐ плоскость пересекает ось конуса под углом большим либо равным нуля, но меньше угла наклона образуящей конуса (плоскость Q).
α
ТП2
ГП2
QП2РП2 |
RП2 |
Рис. 6.12 |
|
90
