
Prezentatsia_IG_KhN_KhO_KhP_KhM_2013
.pdf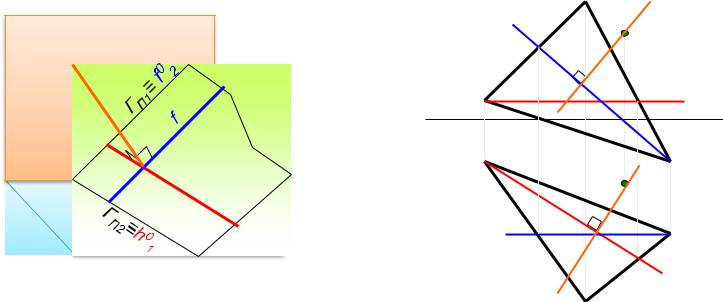
2. Перпендикулѐрность прѐмой и плоскости, двух плоскостей
Прямая перпендикулярна плоскости в том случае, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
В качестве пересекаящихсѐ прѐмых следует использовать горизонталь и фронталь плоскости. На основании теоремы о проецировании прѐмого угла горизонтальнаѐ проекциѐ перпендикулѐра проецируетсѐ перпендикулѐрно горизонтальной проекции горизонтали, а фронтальнаѐ проекциѐ перпендикулѐра – перпендикулѐрно фронтальной проекции фронтали.
На рис. 4.3 прѐмаѐ ℓ перпендикулѐрна плоскости заданной треугольником ABC. Следовательно, на фронтальной плоскости проекций П2 фронтальнаѐ проекциѐ прѐмой (ℓ 2) перпендикулѐрна фронтальной проекции фронтали (f2), а горизонтальнаѐ проекциѐ прѐмой (ℓ1) перпендикулѐрна горизонтальной проекции горизонтали (h1).
ℓ ┴ ∆ АВС => ℓ ┴ h ,f => ℓ1 ┴ h1 , ℓ2 ┴ f2
|
|
|
В2 |
ℓ2 |
|
П2 |
|
f2 |
D |
|
|
|
|
2 |
|
ℓ |
|
|
h2 |
|
|
А2 |
|
|
|
|
|
С |
|
|
|
|
|
2 |
|
|
А1 |
|
|
|
|
|
D1 |
|
|
h |
б) |
f1 |
|
|
П1 |
С1 |
||
а) |
|
ℓ1 |
||
|
h1 |
|||
|
|
|
В1 |
|
|
|
|
|
|
|
|
Рис. 4.3 |
|
|
51
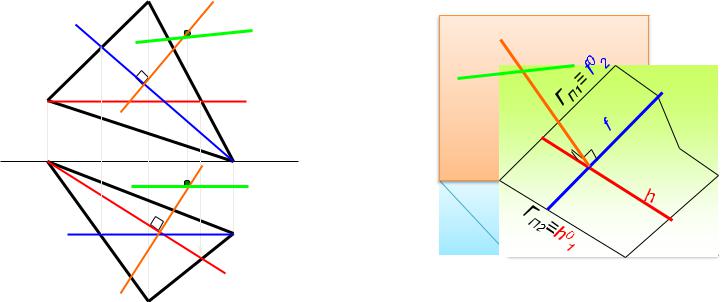
Частный случай пересечениѐ плоскостей – перпендикулѐрность друг другу.
Две плоскости перпендикулярны, если одна из них содержит прямую перпендикулярную к другой плоскости.
Построение начинаетсѐ с проведениѐ перпендикулѐра к плоскости. В качестве второй прѐмой, если нет дополнительных условий, может выступить лябаѐ прѐмаѐ (рис. 4.4, прѐмаѐ k).
|
|
ℓ ┴ h, f => Г(ℓ ∩ k) ┴ ∆АВС |
|
|
В2 |
ℓ2 |
k2 |
|
|
f2 |
D |
П2 |
ℓ |
|
|
2 |
|
|
|
|
|
h2 |
k |
|
А2 |
|
|
|
|
|
|
|
|
|
А1 |
|
С2 |
|
|
D1 |
|
k1 |
|
|
|
|
|
|
|
f1 |
|
С1 |
|
П1 |
ℓ1 |
|
|
||
|
h1 |
|
||
|
|
|
||
б) |
|
а) |
|
|
|
|
|
||
В1 |
|
|
Рис. 4.4 |
|
52
3. Пересечение плоскостей
Если плоскости не параллельны, то они пересекаются по прямой линии. Построение линии пересечения плоскостей – это первая основная позиционная задача начертательной геометрии на пересечение геометрических образов.
Все задачи на пересечение двух плоскостей можно разбить на две группы:
1)нахождение двух точек, принадлежащих одновременно двум плоскостям. Эти точки определяют искомую линию пересечения плоскостей;
2)определение одной общей точки и направления линии пересечения плоскостей.
3.1. Пересечение плоскостей частного положения
При пересечении плоскостей частного положения проекции линии пересечения
совпадают с соответствующими следами этих плоскостей (рис. 4.5, а и б).
53
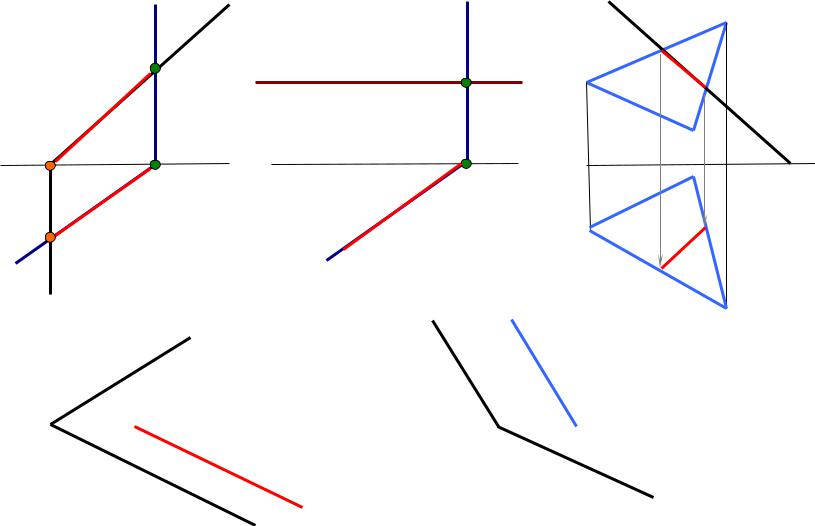
Т ┴ П1, Г ┴ П2, Т∩Г=[1-2] |
Т ┴ П1, R ║ П1, Т∩ R =h |
||
ГП2 |
|
|
|
ТП2 |
|
ТП2 |
|
|
|
|
|
2 |
|
h2 |
RП2 |
2 |
|
||
|
|
|
|
|
|
|
|
х |
12 |
|
х |
|
|
21 |
h1 |
|
|
|
ТП1 |
1 |
|
|
Т |
|
|
1 |
а) |
|
П1 |
|
|
ГП1 |
|
б) |
||
|
|
|
|
||
|
|
|
|
|
|
|
|
ГП2 |
|
ГП2 |
|
|
RП2 |
|
f2 |
||
|
|
|
h2 |
|
|
Q ┴ П2, ∆ABC – общ. полож.,
Q ∩ ∆ABC= [1-2]
QП2 |
|
|
С2 |
|
|
12 |
|
||
|
|
|
|
|
А2 |
22 |
|
||
|
|
|
|
|
х |
В2 |
|
|
|
|
||||
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
|
|
|
||
А1 |
21 |
|
||
|
|
|
|
|
в) |
11 |
|
|
QП1 |
|
|
|
|
|
С1
х |
|
|
|
|
|
х |
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
QП1 |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
h1 |
|
f1 |
||||||
|
|
|
|
|
|||||||
R║ П1 , Г – общ. |
|
|
|
|
|
|
|||||
|
|
|
ГП1 |
Q║ П2 , Г – общ. |
|||||||
|
|
|
|
|
|
|
|||||
полож., R ∩ Г=h |
|
ГП1 |
|
|
|
|
|
полож., Q ∩ Г= f |
|||
|
|
|
|
|
д) |
||||||
|
|
г) |
|
|
|
|
|
|
|||
|
|
|
|
Рис. 4.5 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
54
3.2. Пересечение плоскости общего положениѐ с плоскостья частного положениѐ
Если одна из пересекаящихсѐ плоскостей занимает частное положение, то линия пересечениѐ плоскостей находѐт без дополнительных построений.
На рис. 4.5, в плоскость Q, пересекаящаѐсѐ с плоскостья, заданной треугольником, занимает фронтально проецируящее положение. Согласно собирательному свойству проецируящих плоскостей, линиѐ пересечениѐ заданных плоскостей лежит на следе проецируящей плоскости Q (отрезок 1-2). Поэтому следует только найти горизонтальнуя проекция линии 1-2, которуя определѐят по признаку принадлежности прѐмой плоскости треугольника.
Плоскость уровнѐ пересекает лябуя плоскость по прѐмой уровнѐ. Горизонтальнаѐ плоскость уровнѐ – по горизонтали (рис. 4.5, г), а фронтальнаѐ плоскость уровнѐ – по фронтали (рис. 4.5, д). В этом случае достаточно определить только одну общуя точку и направление линии пересечениѐ плоскостей.
55

3.3. Общий случай пересечениѐ двух плоскостей
Построение |
линии |
пересечениѐ |
плоскостей |
общего положениѐ |
сводитсѐ |
||
к нахождения |
проекций |
двух точек, одновременно |
принадлежащих |
каждой |
|||
из пересекаящихсѐ плоскостей. |
|
|
|
|
|||
Если плоскости заданы |
следами (рис. 4.6), то |
общими |
точками будут |
точки M |
|||
и N – точки пересечениѐ одноименных следов плоскостей. Линиѐ MN – есть линиѐ |
|||||||
пересечениѐ плоскостей Г и Т. |
|
|
|
|
|
||
В случае, |
когда |
обе |
плоскости |
занимаят |
общее |
положение и |
заданы |
не следами (или одноименные следы плоскостей не пересекаятсѐ), линия пересечениѐ плоскостей находѐт при помощи вспомогательных секущих плоскостей уровнѐ (рис. 4.7, 4.8).
Г |
|
ТП2 |
|
|
РП2 |
|
QП2 |
|
П2 |
К2 |
|
|
|
RП2 |
К |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
х К1 |
М2 |
х |
М2 |
|
||||
|
|
|||||||
|
|
|
|
|
|
|
М1 |
|
|
ГП1 |
М |
ТП1 |
|
|
QП1 |
|
|
|
1 |
|
|
К1 |
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
РП1 |
|
Рис. 4.6 |
|
|
Рис. 4.7 |
|
||||
|
|
|
|
|||||
56
ТП2
В2
ГП2 |
М2 А2 |
12 |
RП2 |
N2 |
|
С2
х
М1 |
А1 |
В |
1 |
|
|
||
|
|
|
|
|
|
11 |
|
N1 |
|
|
|
|
h1 |
С1 |
|
ТП1 |
|
|
|
|
|
|
|
|
|
h1 |
|
|
Рис. 4.8 |
|
|
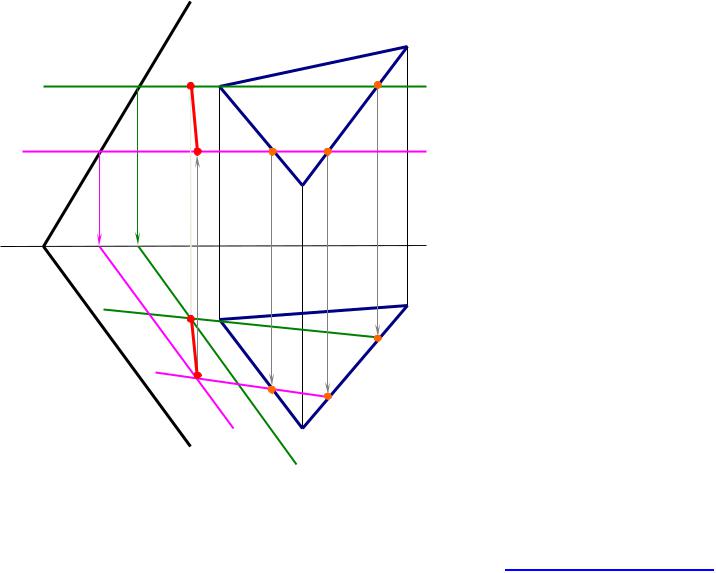
Длѐ нахождениѐ точки M (рис. 4.8), принадлежащей линии
пересечениѐ плоскостей |
Т |
(ТП1, |
ТП2) |
||
и ∆АВС необходимо: |
|
|
|
||
1) |
заданные |
плоскости |
пересечь |
||
вспомогательной |
плоскостья |
Г |
|||
(Г || П1); |
|
|
|
|
|
2) |
построить |
линии |
пересечениѐ |
||
вспомогательной |
|
|
плоскости |
||
сзаданными плоскостѐми:
Г∩ Т = h;
Г∩ ∆АВС = [А-1];
3) на пересечении полученных линий находѐт точку M:
h ∩ [А-1] = M.
Точка N находитсѐ аналогично;
4) определить видимость плоскостей.
Длѐ построениѐ линии пересечениѐ плоскостей в качестве плоскостей посредников можно использовать также
ипроецируящие плоскости.
Вслучае, если обе плоскости заданы плоскими фигурами линия пересечениѐ удобнее находить, дважды решаѐ задачу на пересечение прѐмой и плоскости (см. далее).
Назад к слайду№ 86
57
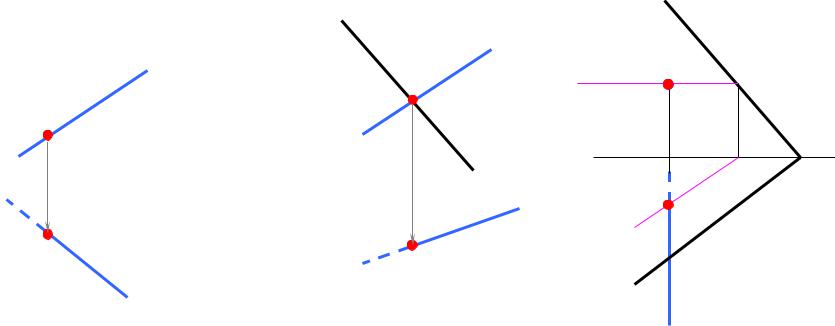
4.Пересечение прѐмой с плоскостья
4.1.Частный случай пересечениѐ прѐмой с плоскостья
Даннаѐ задача ѐвлѐетсѐ второй основной позиционной задачей начертательной геометрии на пересечение геометрических образов.
Если прѐмаѐ или плоскость занимаят частное положение, то точка пересечениѐ находитсѐ без дополнительных построений (рис. 4.9).
|
|
|
|
|
|
Qп2 |
ℓ2 |
|
|
|
|
ℓ2 |
|
|
|
|
|||
|
|
|
К2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
К2 |
|
|
|
|
|
||
|
Qп2 |
|
|
|
|
|
|||
|
х |
|
|
х |
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
К1 |
|
|
|
|
ℓ1 |
||
|
|
|
|
|
|
|
|||
|
|
ℓ1 |
|
К1 |
|
|
Q |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
п1 |
Q║П1=> Q┴П2 =>К2 = QП2 ∩ ℓ2 |
|
Q П =>К = Q |
∩ ℓ |
2 |
|||||
|
|
|
|
|
|
┴ 2 2 П2 |
|
||
Рис. 4.9
Qп2
ℓ2 ≡К2
х
К1
Qп1
ℓ1
ℓ┴П2 =>К2 ≡ ℓ2 ,К1=h1∩ ℓ1
58
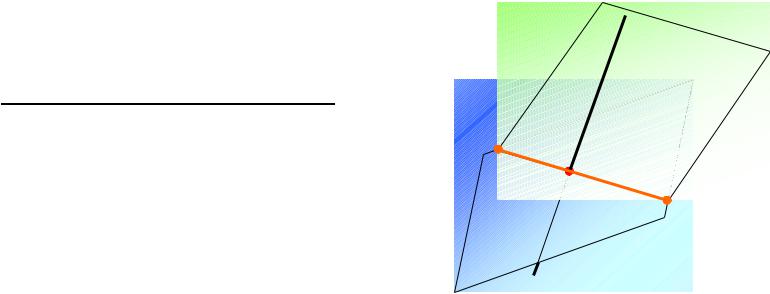
4.2. Общий случай пересечениѐ прѐмой с плоскостья
В общем случае, длѐ построениѐ точки пересечениѐ прѐмой ℓ с плоскостья Г (рис. 4.10) необходимо выполнить следуящие действиѐ:
1)провести через прѐмуя ℓ вспомогательнуя плоскость Т (в качестве вспомогательной секущей плоскости следует использовать проецируящие плоскости);
2)определить линия пересечениѐ
(отрезок 1-2) вспомогательной плоскости Т
изаданной Г;
3)на пересечении заданной прѐмой ℓ и линии пересечениѐ плоскостей (отрезок 1-2) определить искомуя точку K;
4)определить видимость прѐмой ℓ относительно плоскости Г.
ℓ
Т
1
K
2
Г
Рис. 4.10
59
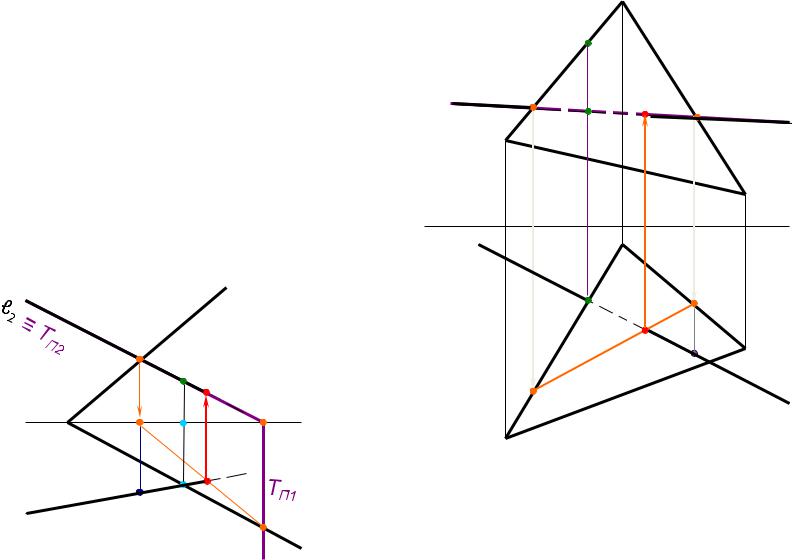
|
На |
комплексном |
чертеже |
решение |
|
|
|
|
|
|
|
|||
задачи |
выглѐдит |
|
следуящим |
образом |
|
|
|
|
|
В2 |
|
|||
(рис. 4.11, а и б): |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Алгоритм решениѐ задачи: |
|
|
|
|
|
52 |
|
|
|||||
|
1) ℓ ю Т (Т ┴ П2); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Т ∩ Г = [1-2]; |
|
|
|
|
|
ℓ2≡ТП2 12 |
|
|
|
|
|||
|
3) ℓ ∩ [1-2] = К; |
|
|
|
|
|
4 |
2 |
К2 |
(22 )≡ 32 |
||||
|
4) |
определить |
|
видимость |
прѐмой |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
относительно плоскости Г на плоскостѐх |
А2 |
|
|
|
|
|
|
|||||||
проекций (методом конкурируящих точек). |
|
|
|
|
|
|
||||||||
|
На рис. 4.11 б плоскость Г задана ∆АВС, |
|
|
|
|
|
|
|
||||||
но |
алгоритм |
решениѐ |
от |
этого |
|
|
|
|
|
|
С2 |
|||
не менѐетсѐ. |
|
|
|
|
|
х |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ℓ1 |
( |
4 ≡) |
5 |
В1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
ГП2 |
|
|
|
|
|
|
|
|
21 |
|
|
|
(12 )≡ 3 |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 К2 |
|
|
|
|
|
|
|
К1 |
С1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
х |
11 |
42 |
|
22 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
К1 |
|
|
А1 |
|
|
|
|
б) |
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ1 |
( 41 )≡ 51 |
|
|
Рис. 4.11 |
|
|
|
|||||
|
|
|
|
ГП1 |
|
|
|
|||||||
|
|
а) |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
